• 본 글은 다음의 교재를 참고하여 작성되었습니다. - "Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, P177~P189"

사용한 코드는 여기서.
https://www.kaggle.com/code/smarcle/ch6-decisiontree

DecisionTree

디시전트리는 일정한 기준에 따라 하나의 트리를 형성하며 분류 또는 회귀를 수행하는 모델입니다.
보통 계산 복잡도는 O(log2(m)).

예측

아이리스 데이터셋에 대해 예측한 결과.

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris(as_frame=True)
X_iris = iris.data[["petal length (cm)", "petal width (cm)"]].values
y_iris = iris.target

tree_clf = DecisionTreeClassifier(max_depth = 2, random_state=42)
tree_clf.fit(X_iris, y_iris)

from sklearn.tree import export_graphviz

export_graphviz(tree_clf, out_file="iris_tree.dot", feature_names=["꽃잎 길이 (cm)", "꽃잎 너비 (cm)"], class_names=iris.target_names, rounded=True, filled=True)

from graphviz import Source

Source.from_file("iris_tree.dot")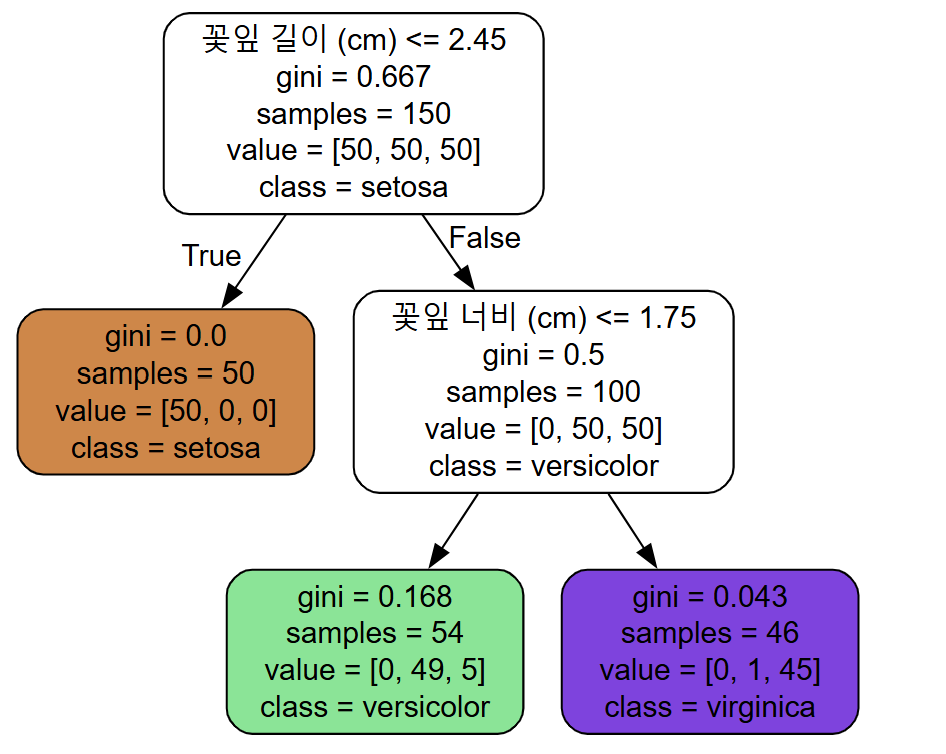

지니 불순도 : 한 노드에 있는 모든 샘플 중 얼마나 같은 클래스에 속해있는지를 의미함, 모든 샘플이 같은 클래스라면 gini=0

샘플 : 얼마나 많은 트레인 샘플이 적용되었는가
그림에서 오른쪽 처음 false나온 노드의 경우 100개의 샘플이 꽃입 길이가 2.45보다 길다.

value : 각 클래스에 얼마나 많은 샘플이 있었는지
50, 50, 50이면 여기선느 setosa 50개, versicolor 50개, virginia 50개.

클래스 확률 추정

tree_clf.predict_proba([[5, 1.5]]).round(3)
>>> array([[0.   , 0.907, 0.093]])

tree_clf.predict([[5, 1.5]])
>>> array([1])

특정 데이터를 주고, 이 데이터가 어떤 클래스에 속하는지 확률 추정 가능.
길이 5 너비 1.5라면 0번째 클래스 - 0%, 1번째 - 90.7%, 2번째 - 9.3%
클래스 하나만 예측해야 한다면 1번 클래스로 예측됨.

cart 훈련 알고리즘

탐욕 알고리즘의 일종.
디시전 트리 학습에 주로 활용됨.
특성 하나 k의 임계값 t를 기준으로 트레이닝 셋을 둘로 나누는 방법.
이런 식으로 불순도를 더 이상 줄일 수 없을때까지 나누는 방식

규제 매개변수

max_features : 각 노드에서 분할에 사용할 특성의 최대 갯수
max_leaf_nodes : 클래스 수
min_samples_split : 노드의 분할을 위한 최소 샘플 수
min_samples_leaf : 리프 노드 생성에 필요한 최소 샘플 수

이런 하이퍼파라미터들을 사용하면 형태를 어느 정도 제한할 수 있어 과적합 등을 피하는 것도 가능.

회귀

랜덤으로 수 생성해서 회귀 돌리기.

import numpy as np
from sklearn.tree import DecisionTreeRegressor

np.random.seed(42)
X_quad = np.random.rand(200, 1) - 0.5
y_quad = X_quad ** 2 +0.025 * np.random.randn(200, 1)

tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X_quad, y_quad)

export_graphviz(tree_reg, out_file="quad.dot", rounded=True, filled=True)

Source.from_file("quad.dot")

분류에도 쓸 수 있지만, 회귀에도 사용 가능.

난점 : 분산 문제

일반적으로 디시전트리의 분산은 상당히 커서, 하이퍼파라미터나 데이터를 살짝만 건드려도 모델이 180도 달라지는 경우가 많다.
이를 개선한 부분이 바로 랜덤포레스트로, 디시전트리를 여러 개 돌려서 그 평균을 결과로 사용하는 방식.