• 본 글은 다음의 교재를 참고하여 작성되었습니다. - "Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, P113~P143"

이번에도 아직 미리캔버스 사진 작업 밀린 부분이 많아서 이번 주도 velog로 대체해서 올립니다.
사실 편한건 velog긴 한데 네이버블로그 쪽을 한번 각잡고 써놓으면 귀찮을 일은 없더라구요...

https://www.kaggle.com/code/smarcle/regression
실습해본 노트북은 이쪽.

Regression

머신러닝으로 해결 가능한 문제 중 대표적인 것으로는 회귀 문제와 분류 문제가 있음.
회귀 문제는 지도 학습 방식을 주로 활용하며, 데이터들의 컬럼들을 이용해 레이블에 있는 타깃값을 최대한 정확히 예측해내는 것이 핵심.

데이터셋

import numpy as np

np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1)
y = 4 + 3 * X + np.random.randn(m, 1)

X[0]

골때리게도 자체 생성했다. 와...
그리고, 이 데이터는 가우스 잡음이 끼어있다.
전기회로 때 들었던 그 '잡음'에 해당하는거 맞다.
데이터에 잡음이 많다면, 정확한 예측이 힘들어지는 경향이 있다.

덕분에 네이버 블로그 쪽에 올리는 용도로는 house price 사용 예정.

아무튼 이 데이터셋에 대해 우리는 선형 회귀를 사용할건데, 하이퍼파라미터 세타를 찾는게 파인 튜닝 시의 목표다.
이 세타를 찾는 방법 중 정규 방정식을 사용하는 게 있다.

from sklearn.preprocessing import add_dummy_feature

X_b = add_dummy_feature(X)
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y

theta_best

그리고 이 코드가 정규 방정식 코드고, 비용함수를 최소화하는 최적의 하이퍼파라미터 세타를 찾아준다.

그리고 그걸 넣어서 예측을 돌리고, 그래프를 뽑으면 이렇다.

X_new=np.array([[0], [2]])
X_new_b = add_dummy_feature(X_new)
y_predict = X_new_b @ theta_best
y_predict

import matplotlib.pyplot as plt
plt.plot(X_new, y_predict, "r-", label="에측")
plt.plot(X, y, "b.")
plt.show()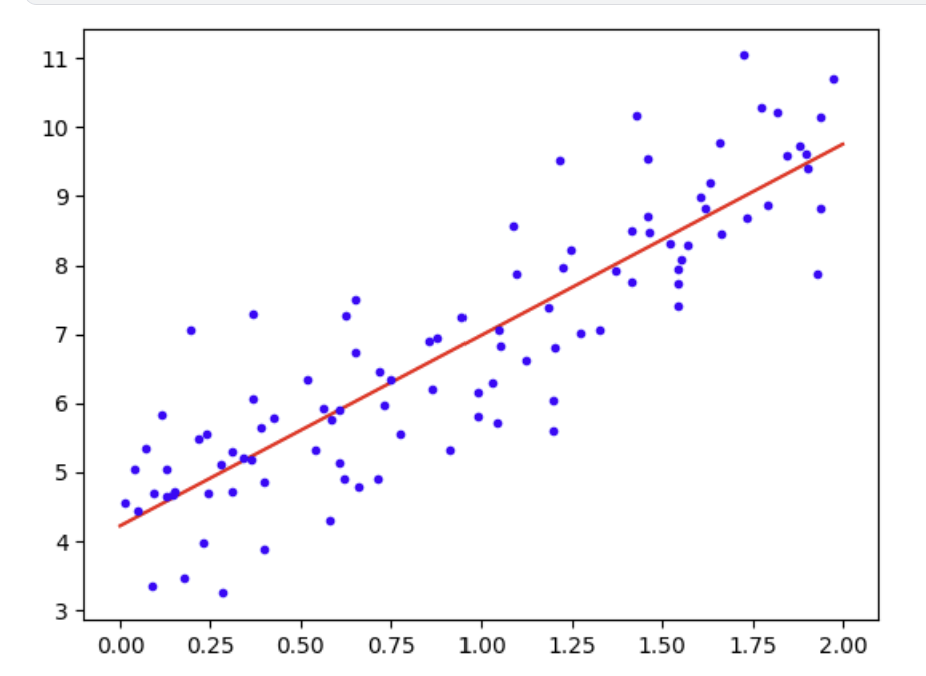

회귀 문제는 대개 저 빨간 선을 찾는게 핵심. 저 선이 예측 값들을 모아놓은 선이라고 생각하면 편하다.

LinearRegression

아까 한 선형회귀를 사이킷런 내에서 지원하는 모델로 진행한 것.

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_

lin_reg.predict(X_new)

모델 끌어와서, .fit로 데이터 학습시키고, .predict로 테스트 데이터에 대해 돌리면 끝.

특징으로는, 여기서 가중치(coef)와 편향(intercept)도 따로 저장이 된다. 따라서 이걸 이용해서 선형대수학 때 했던 것 같은 SVD라거나 그런걸 해볼 수 있는 것같은데 수학을 못하니 설명은 불가.
대신 코드는 이렇다.

theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd

경사하강법

간단히 말하자면 그래프 내 극솟값을 찾아가는 방법. 이것도 종류가 다양하다.

배치 경사 하강법

매번 데이터 전체에 대해 연산을 진행하는 특징을 가진 방법.

eta=0.1
n_epochs=1000
m=len(X_b)
np.random.seed(42)
theta=np.random.randn(2, 1)
for epoch in range(n_epochs):
    gradients = 2/m*X_b.T@(X_b@theta-y)
    theta=theta-eta*gradients
    
theta

결과는 array([[4.21509616],
[2.77011339]])
안타깝게도 사이킷런 내에서 이 배치 경사하강법을 직접적으로 지원하지는 않는다.

확률적 경사 하강법

아까와는 반대로 데이터 중 랜덤으로 선택해 연산을 진행하는 방법.
매 반복에서 다뤄야 할 데이터가 비교적 적기 때문에 좀 더 효율적이고 빠르게 결과를 도출해낼 수 있지만, 문제는 '확률적'이라 대개는 전체 최솟값을 찾을 확률이 떨어진다.
다만, 꽤 괜찮은 최솟값을 항상 찾아내주기는 한다.

n_epochs=50
t0, t1 = 5, 50
def learning_schedule(t):
    return t0/(t+t1)
np.random.seed(42)
theta=np.random.randn(2, 1)

for epoch in range(n_epochs):
    for iteration in range(m):
        random_index = np.random.randint(m)
        xi=X_b[random_index:random_index+1]
        yi=y[random_index:random_index+1]
        gradients=2*xi.T@(xi@theta-yi)
        eta = learning_schedule(epoch*m+iteration)
        theta=theta-eta*gradients

theta

결과는 array([[4.21076011],
[2.74856079]])
아까 배치 방식이랑 비교해보면, 비슷한 결과가 나오는데도 에포크는 50만 돌렸다. 즉 20배 이득.

SGDRegressor

사이킷런 내에서 제공하는 확률적 경사하강법 모델.
이쪽을 이용하는게 보통은 편하다.

from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-5, penalty=None, eta0=0.01, n_iter_no_change=100, random_state=42)
sgd_reg.fit(X, y.ravel())

미니배치 경사 하강법

데이터셋을 작은 묶음 '미니배치'로 만들어서 여기에 대해 SGD를 쓰는 방식.
장점은 전체 최솟값을 찾아내기는 더 쉬워진다는것.
단점은 로컬 극솟값에서 빠져나오기도 힘들다는것.

다항 회귀

아까 그 데이터는 직선형으로 예측이 나왔지만, 모든 데이터가 직선형으로 나오지는 않는다.
하지만, 이런 경우에도 문제없이 선형 모델들을 사용 가능하다.

np.random.seed(42)
m=100
X=6*np.random.rand(m, 1)-3
y=0.5*X**2+X+2+np.random.randn(m, 1)

더 복잡한 데이터 등장. 똑같이 랜덤 생성했고, 이번에는 이차함수꼴로 곡선형으로 나올 예정이다.

여기서 사이킷런 내 기능 중 하나인 PolynomialFeatures를 이용해 새로운 특성인 '각 특성의 제곱'을 추가해보았다.

from sklearn.preprocessing import PolynomialFeatures
poly_features=PolynomialFeatures(degree=2, include_bias=False)
X_poly=poly_features.fit_transform(X)
X_poly[0]

그리고 아까처럼 선형회귀를 돌리면 이렇게 된다.

lin_reg=LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_

결과는 (array([1.78134581]), array([[0.93366893, 0.56456263]]))

학습 곡선

훈련 오차와 검증 오차를 에포크에 따라 함수로 나타낸 그래프.
보통 사이킷런 내에 있는 learning_curve 함수를 사용하면 얻을 수 있다.

from sklearn.model_selection import learning_curve
train_sizes, train_scores, valid_scores =learning_curve( LinearRegression(), X, y, train_sizes=np.linspace(0.01, 1.0, 40), cv=5, scoring="neg_root_mean_squared_error")
train_errors=-train_scores.mean(axis=1)
valid_errors=-valid_scores.mean(axis=1)

plt.plot(train_sizes, train_errors, "r-+", linewidth=2, label="훈련 세트")
plt.plot(train_sizes, valid_errors, "b-", linewidth=3, label="검증 세트")
plt.show()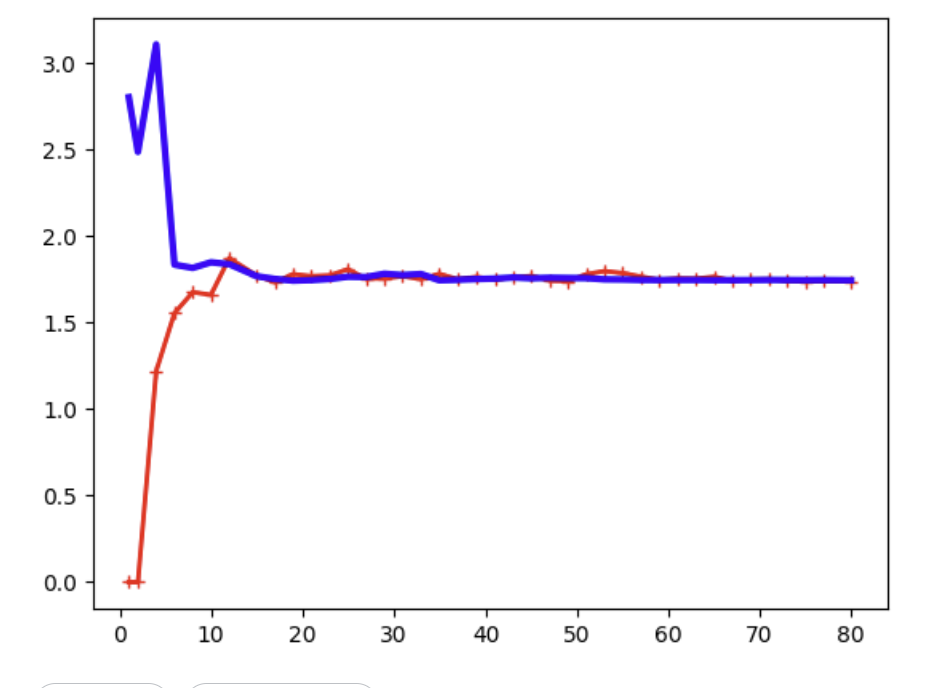

그러면 그래프가 이렇게 나온다.
이 그래프는 아쉽게도 과소적합 그래프인데, 빨간색 선(훈련 오차)이 값이 초반에는 0이었다 급격하게 증가한다.

from sklearn.pipeline import make_pipeline
polynomial_regression=make_pipeline(PolynomialFeatures(degree=10, include_bias=False), LinearRegression())

train_sizes, train_scores, valid_scores=learning_curve(polynomial_regression, X, y, train_sizes=np.linspace(0.01, 1.0, 40), cv=5, scoring="neg_root_mean_squared_error")
train_errors=-train_scores.mean(axis=1)
valid_errors=-valid_scores.mean(axis=1)

plt.plot(train_sizes, train_errors, "r-+", linewidth=2, label="훈련 세트")
plt.plot(train_sizes, valid_errors, "b-", linewidth=3, label="검증 세트")
plt.show()

같은 데이터로, 10차 다항회귀를 돌린 모습.

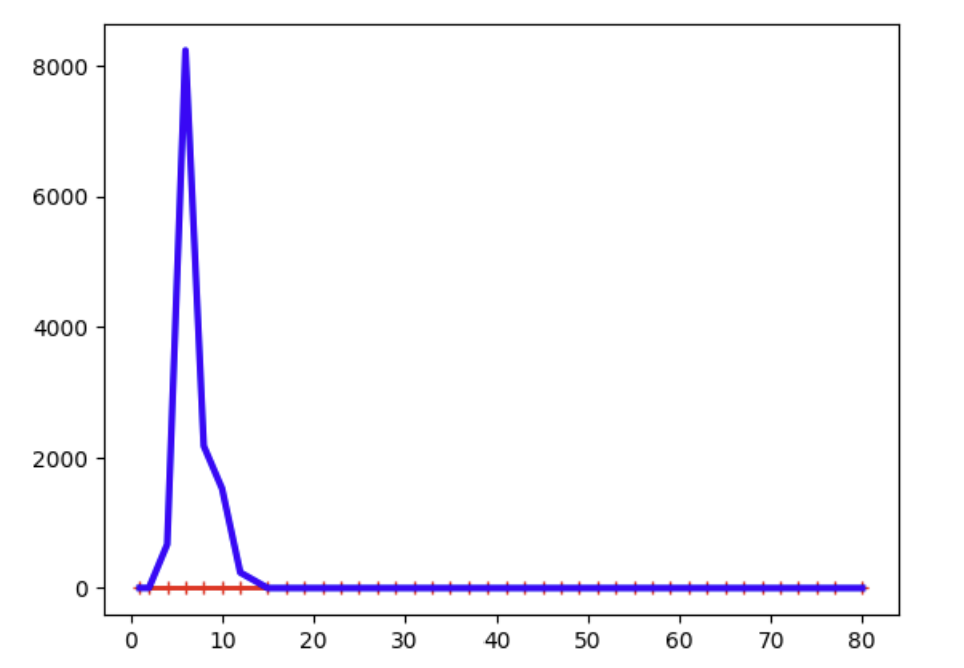
그래프를 어느 정도 조정해서 확인해본다면 알겠지만, 이 경우는 비교적 오차가 이전에 비해 작다.

규제가 있는 선형 모델

교재에서는 다음과 같은 3가지 모델을 소개한다.

• 릿지 회귀
  모델의 가중치를 가능한 작게 유지하는 방식으로 규제를 적용한 모델. 훈련이 끝나면 규제가 없는 MSE 또는 RMSE를 활용해 평가한다.
  주로 스탠다드 스케일러를 사용한 뒤 사용하며, 사이킷런 내 Ridge 함수로 사용.

• 라쏘 회귀
  비교적 덜 중요한 특성의 가중치를 제거하는 방향으로 규제를 적용한 모델.
  이쪽도 훈련이 끝나면 MSE 또는 RMSE를 활용해 평가한다.
  주로 스탠다드 스케일러를 사용한 뒤 사용하며, 사이킷런 내 Lasso 함수로 사용. 혹은, SGDRegressor에서 penalty="l1", alpha=0.1을 사용하면 똑같이 사용 가능하다.

• 엘라스틱넷
  앞 2개의 절충안. 전반적으로 가중치를 작게 하면서도 중요하지 않은 특성의 가중치를 더 줄인다.
  2개의 혼합 정도는 r이라는 특성을 이용해 조절하며, r=0이면 완전한 릿지 회귀 / 1이면 완전한 라쏘 회귀라고 봐도 무방한 수준.
  사이킷런 내 ElasticNet 함수로 사용 가능하다.

• 조기종료하기
  간단하게, 학습을 진행하다 검증 오차가 최솟값이 되는 순간 앞으로 몇번의 학습을 더 해야 하건 바로 학습을 중지시켜버리는 방법. 특성상 과적합 방지에 효과적이다.