• 본 글은 다음의 교재를 참고하여 작성되었습니다. - "Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, P144~P152"

Logistic Regression

1)작동 방식 - 확률 추정

로지스틱 회귀(Logistic Regression)는 데이터가 특정 클래스에 속할 가능성을 추정하는 회귀 알고리즘입니다. 추정 확률이 50% 미만이면 0, 이상이면 1로 값을 예측하는 방식으로 작동합니다.

비슷한 방식으로 작동하는 선형 회귀가 있지만, 심플하게 입력값 X 가중치 + 바이어스 형태의 직선 방정식을 사용하는 선형 회귀와는 달리 로지스틱 회귀는 위 직선에서 얻은 값을 시그모이드 함수를 거쳐 활용합니다.

$p=h_θ(x)=σ(x^Tθ)$
위 수식은 추정확률 p를 나타낸 것으로, σ(x)는 시그모이드 함수를 의미합니다.
$σ(x)=\frac{1}{1+exp(-t)}$
그리고 이 수식이 시그모이드 함수입니다. 아래 그래프와 같은 형태를 가지는 함수로, 값이 무조건 0과 1 사이에 위치하게 됩니다.

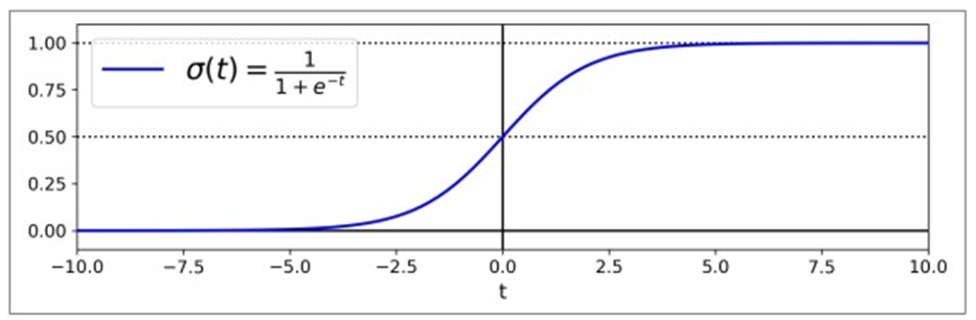
그리고 이런 과정을 통해 구한 추정확률 p에 대해 가운데 0.5 선을 기준으로 예측값 y를 다음과 같이 구할 수 있습니다.
$y=\begin{cases}0\;\;if\;\;p<0.5\\1\;\;if\;\;p>=0.5\end{cases}$

위 그림에서 보다시피 t>=0일 때 1로 예측하고, t<0일 때 0으로 예측하는 방식입니다.

• 여기서 p를 logit 또는 log-odds라고 부르기도 하는데, $logit(p)=log\frac{p}{1-p}$가 시그모이드의 역함수인데다 positive class와 negative class의 가능성에 대한 비율의 로그함수라서 각각 저런 명칭이 생겼다고 하네요.

2)학습 및 비용함수

학습의 최종 목표는 바로 y=1인 경우 높은 확률을 / y=0인 경우 낮은 확률을 가지게 하는 θ값을 설정하는 것입니다. 이는 다음과 같은 비용함수를 가집니다.
$c(θ)=\begin{cases}-log(t)\;\;if\;\;y=1\\-log(1-t)\;\;if\;\;y=0\end{cases}$
위 비용함수를 더 자세히 보면, t가 각각 0과 1로 가까워질 때 어떻게 달라지는지 확인할 수 있습니다.

• t가 0에 가까워지는 경우 - -log(t)가 증가함
• t가 1에 가까워지는 경우 - -log(t)는 0에 수렴함

두 함수 모두 positive class에 대해 1에 가까워지고, negative class에 대해 0에 가까워지는 경우 학습 목표에 일치합니다. 반면 positive class에 대해 1에 가까워지거나, negative class에 대해 0에 가까워지는 경우 비용(오차)가 한없이 증가합니다.

전체 학습 데이터 셋에 대한 비용함수는 모든 학습 데이터 셋에서의 평균 비용입니다. 아래 그림과 같은 수식으로 나타낼 수 있고, 이를 log loss라고 부릅니다.

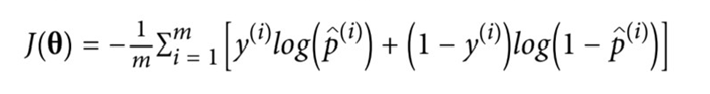
log loss를 최소화하는 θ값을 찾기 위한 closed-form 방정식은 없지만, log loss는 볼록한 형태이기 때문에 Gradient Descent를 이용하면 global minimum을 찾을 수 있습니다.

3)Decision Boundary

예시를 위해 iris 데이터셋을 사용해보았습니다.
해당 데이터셋은 Iris-Virginia를 꽃잎 너비 데이터를 이용하여 구분하는 데이터셋으로, 로지스틱 회귀를 활용하여 Iris-Virginia인지 여부를 예측해보겠습니다.

import numpy as np
import pandas as pd

from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
#iris의 key 출력

X = iris["data"][:, 3:]
y=(iris["target"]==2).astype(np.int64)

from sklearn.linear_model import LogisticRegression

#로지스틱 회귀 활용하여 학습
log_reg = LogisticRegression()
log_reg.fit(X, y)

import matplotlib.pyplot as plt

#그래프 그리는 과정
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba= log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris-Virginia")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris-Virginia")

log_reg.predict([[1.7], [1.5]])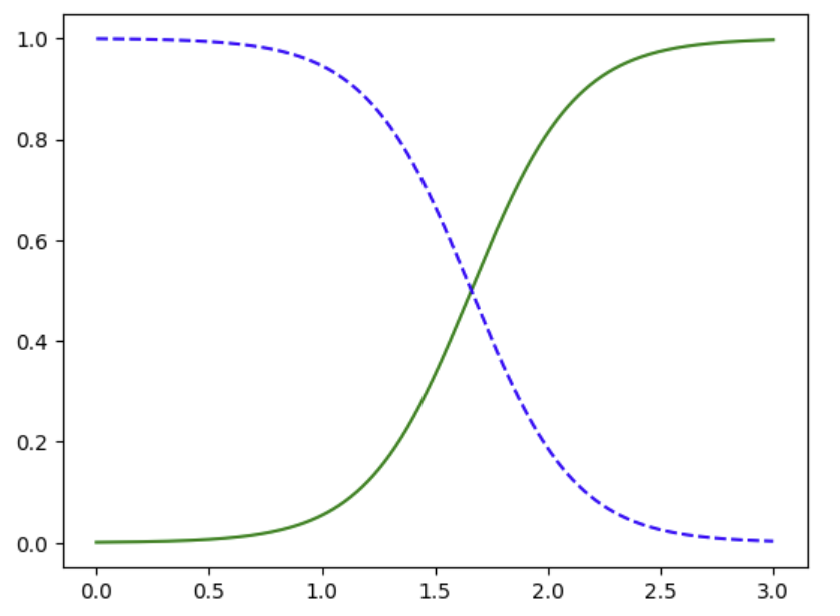

위 그래프에서 파란 점선은 Iris-Virginia가 아닌 경우, 초록 실선은 Iris-Virginia인 경우입니다. 편의상 0/1로 부르겠습니다.
그래프를 보면 0~1cm 언저리까지는 0에 해당하며, 2cm를 넘어가는 경우는 1에 해당합니다.

1.6cm에서는 두 그래프가 만나 확률이 50%인 지점인데, 이 지점이 서로 다른 두 클래스를 구분하는 지점으로, 이 지점을 Decision Boundary라고 칭합니다.

코드 맨 아랫줄 1.7과 1.5에 대해 각각 모델을 돌려보면 1.6을 기준으로 1.7은 True, 1.5는 false가 나오는 것을 확인할 수 있습니다.

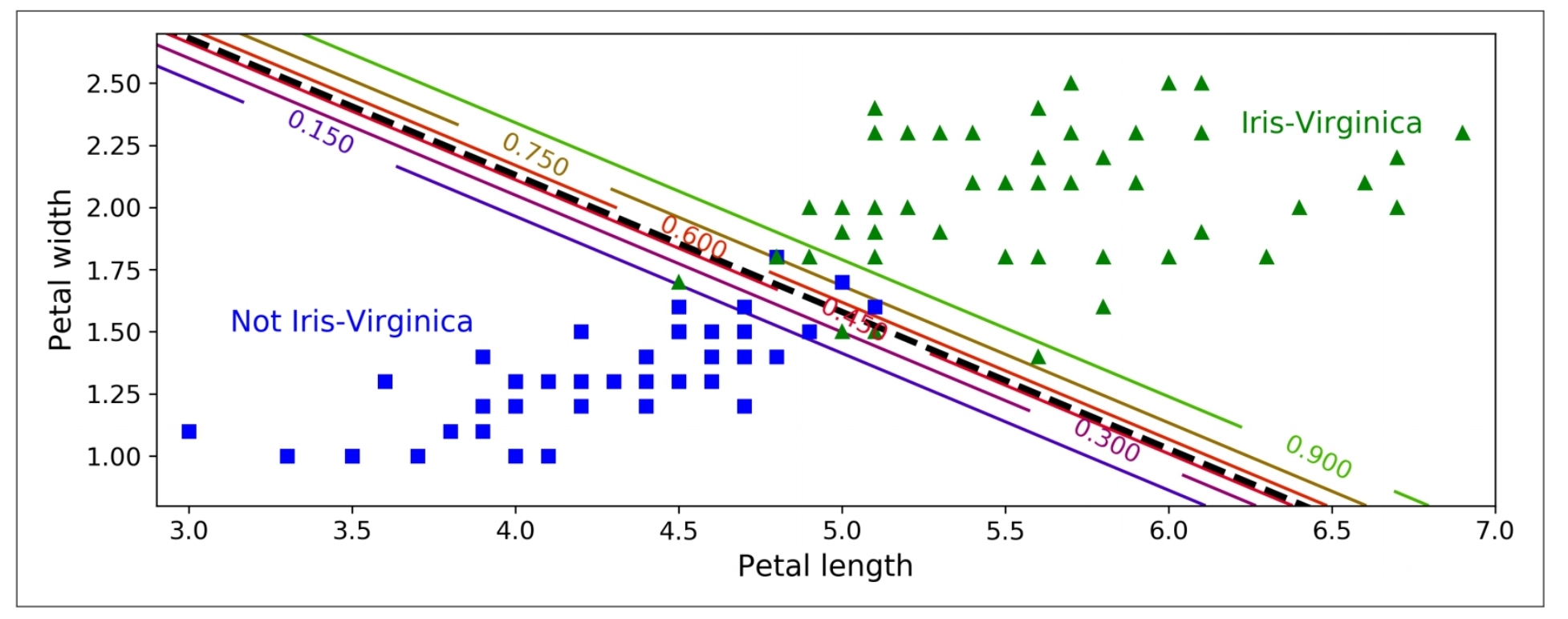
위 그래프는 앞선 코드에서 더 나아가, 꽃잎 너비와 꽃잎 길이라는 2가지 레이블에 대해 로지스틱 회귀를 적용한 그래프입니다.
검은 점선은 Decision Boundary를 의미합니다. 아까 전 경우와는 다르게, 선형 경계로 나타납니다.

4)Softmax Regression

이전에 다루었던 binary classification, Multiclass classification과는 다르게, 로지스틱 회귀는 특별한 방법을 사용하지 않아도 2개 이상의 클래스에 대해 연산할 수 있습니다. 이를 Softmax Regression(소프트맥스 회귀)라고 칭합니다.