- 본 글은 다음의 교재를 참고하여 작성되었습니다. - "Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, P87~P107"
원래는 네이버 블로그에 바로 올려야 맞는데, 아직 미리캔버스 사진 작업 + 이쪽은 모델 하나하나까지 다 분석해서 올려야 하는데다 밀린 부분이 많아서 이번 주는 velog로 대체해서 올립니다.
네이버 블로그쪽도 만괂부~~
Classification
머신러닝으로 해결 가능한 문제 중 대표적인 것으로는 회귀 문제와 분류 문제가 있음.
분류 문제는 지도 학습 방식을 주로 활용하며, 데이터들의 컬럼들을 이용해 레이블에 붙은 카테고리로 분류해내는 것이 핵심.
MNIST 데이터셋
0~9까지의 수를 손글씨로 써서, 이를 28X28 이미지화하고 각 픽셀별로 데이터를 입력해 이를 모아놓은 데이터셋.
분류 문제에 사용하기 적합하며, CNN에 쓰기도 좋음.
https://www.kaggle.com/datasets/oddrationale/mnist-in-csv/data
MNIST 데이터셋.
워낙 유명한 데이터라 변종도 많다.
https://www.kaggle.com/datasets/zalando-research/fashionmnist
숫자 대신 의류 10종으로 분류하는 Fashion-MNIST
https://www.kaggle.com/datasets/andrewmvd/medical-mnist
의료용 사진으로 분류하는 Medical-MNIST
https://www.kaggle.com/datasets/daavoo/3d-mnist
3D-MNIST
작성한 코드(과제용, 추후 네이버 블로그 업로드 시 Convolution'KAN' 만들어서 그걸로 올릴 생각.)
https://www.kaggle.com/code/smarcle/mnist
1. 데이터 분석
데이터 크기는 (70000, 785)인데 train_test_split 이용해서 마지막 레이블 컬럼을 분리하고, 학습용 60000개 / 테스트용 10000개 빼놓음.
import matplotlib.pyplot as plt
def plot_digit(image_data):
image=image_data.reshape(28, 28)
plt.imshow(image, cmap="binary")
plt.axis("off")
some_digit=X[0]
plot_digit(some_digit)
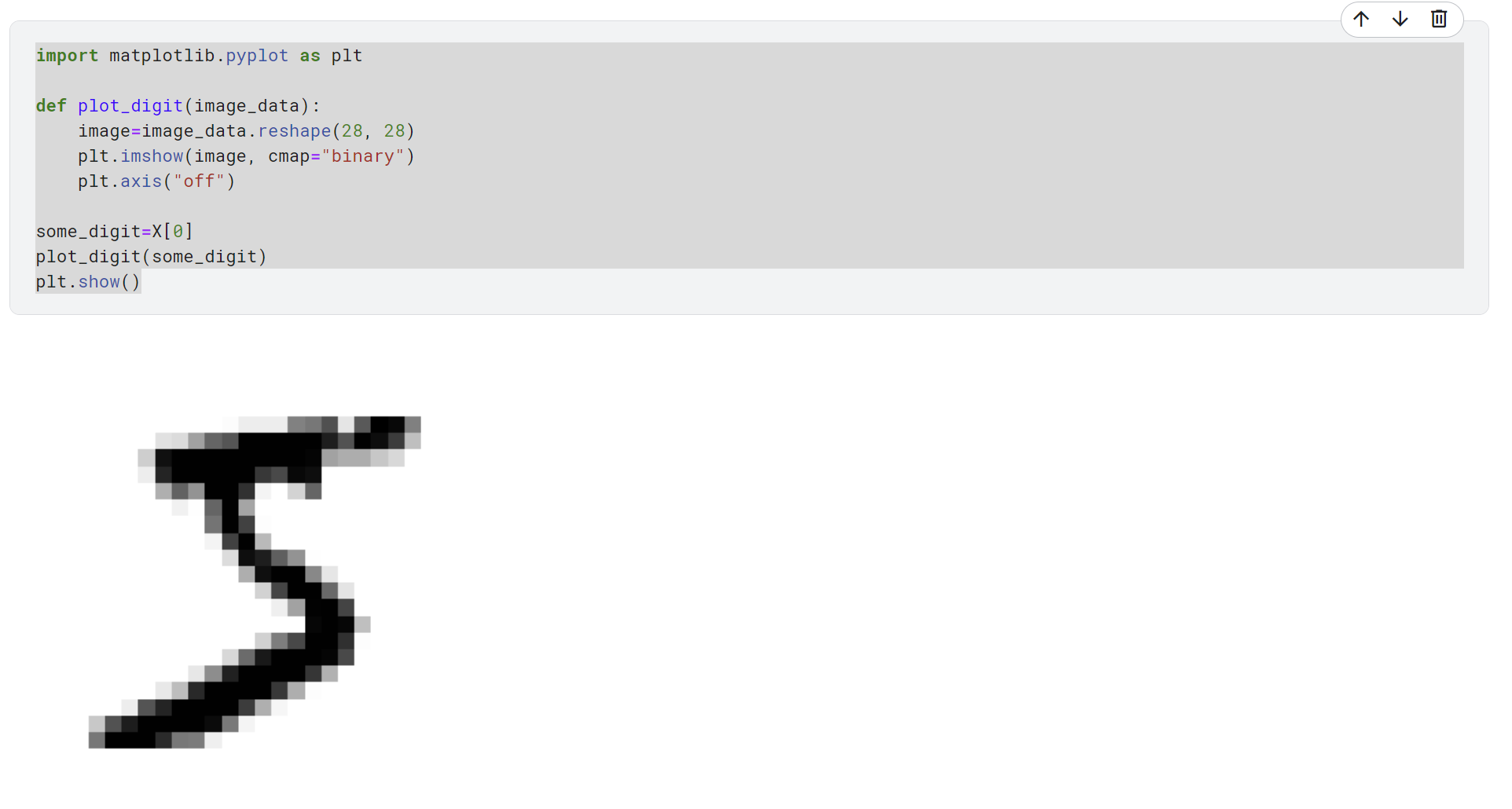
plt.show()이미지는 이런 코드를 이용하면 그릴 수 있는데, 28X28 꼴로 reshape 해서 imshow 사용하면 나온다.
예시로 0번째 이미지를 끌어와봤는데 이건 5.
2. 이진 분류
여러 컬럼을 분류해야 하는 문제라 원래는 multiclass classification을 해야 하지만, 그걸 해야 하는 문제라면 그 수만큼의 이진 분류 문제로도 쪼갤 수 있다.
https://velog.io/@zstep/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9DMultilabel-Classification
Multilabel / multioutput classification에 대한 정리글.
https://blog.naver.com/zstep2014/223586404853
얼마 전 KAN을 이용해 만들어본 이진분류 AI.
y_train_5 = (y_train=='5')
y_test_5 = (y_test=='5')그래서 숫자 5를 기준으로 '5인것'과 '5아닌것'으로 분류하는 방식으로 만들어봤다.
이진 분류에 자주 사용되는 모델인 SGDClassifier를 사용해봤다.
from sklearn.linear_model import SGDClassifier
sgd_clf=SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
sgd_clf.predict([some_digit])SGDClassifier가 지원하는 fit 메소드를 이용해 데이터를 학습시키고, predict 메소드로 아까 그 0번째 데이터 '5'를 넣고 돌려봤다.
결과는 True.
3. 성능 측정
가장 중요한 부분인 성능 측정.
3.1 교차 검증 + 정확도
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")cross_val_score라는 교차 검증 기능을 사용했다.
전체 데이터셋을 cv개로 나누고, 나눠진 각 데이터셋이 돌아가며 테스트 역할을 맡고 그동안 나머지 2개가 학습 데이터가 되는 방식.
최종적으로 cv개의 정확도 평가가 나온다.
문제는 이거 시간이 좀 많이 오래 걸린다.
아무튼 평가 지표를 저번에 피마 인디언 쓸때도 썼던 '정확도'로 해서 돌려봤고, 셋다 95% 이상 나온다.
다만 이런 식으로 1:9 비율로 이진 분류가 나눠지는 경우는 정확도를 쓰는 것이 좋은 선택은 아니다. 위의 경우 전부 '5아님'으로 예측한다고 해도 정확도 90%을 찍기 때문에, 심하게 불균형적인 데이터셋에는 정확도를 평가지표로 잘 사용하지 않는다.
3.2 Confusion Matrix
그래서 우리는 Confusion Matrix를 쓰기로 했어요
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_train_5, y_train_pred)
cm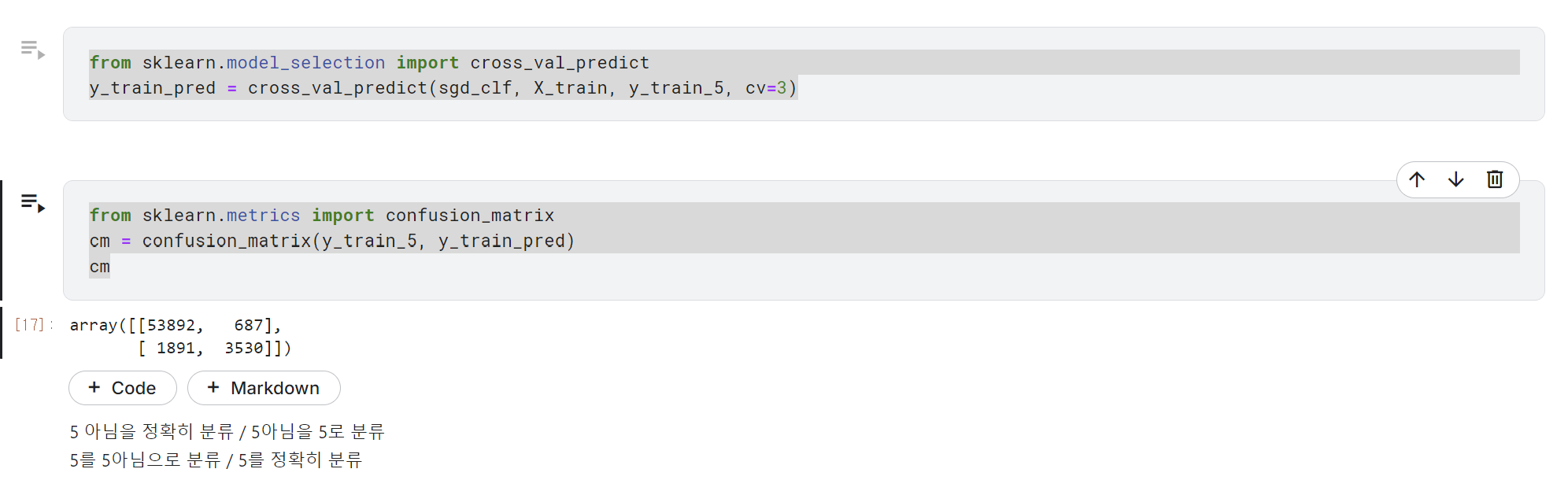
위 코드를 돌리면 이렇게 된다.
먼저 cross_val_predict를 이용해 예측값을 미리 만들어준다. 아까 쓴 cross_val_score랑 사용방식은 비슷한 대신 반환값이 평가 점수가 아니라 예측한 결과 자체다.
그러면 y_train_pred에는 우리가 만든 SGD분류기로 예측한 값이 들어가있을 것이고, y_train_5에는 실제로 5인지 아닌지에 대한 값이 있을 것이다.
confusion_matrix를 사용하면 실제 값과 예측값에 대해 예측값이 맞는 것과 아닌 것의 수를 알려주는 행렬을 뽑아준다.
여기서 실제로 5가 아닌걸 정확히 분류한건 53892개, 5를 정확히 분류한건 3530개. 다만 5를 5아님으로 분류한 경우가 1891개로 좀 많다.
여기서 2가지 개념이 파생된다.
1. 진짜 5를 5로 예측한것 / 일단 5로 예측 들어간 모든것 -> 정밀도 precision
2. 5를 5로 예측한것 / 5건 아니건 예측이 맞는것 -> 재현율 recall
recall은 민감도 또는 TPR이라고도 칭한다.
3.3 precision, recall
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
recall_score(y_train_5, y_train_pred)이런 식으로 사이킷런 내부적으로 지원하는 함수를 이용하면 자동으로 계산해준다.
내 경우는 각각 0.8370879772350012와 0.6511713705958311.
그리고 이 2개의 값을 이용해 F1score를 만들어 사용하는 경우가 많다.
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)내 경우는 값이 0.7325171197343846.
만약 precision, recall 모두 높다면 f1score도 높게 나온다.
하지만 실제 상황에서 precision, recall 중 하나에 좀 더 비중을 두는 경우가 많고, 어느 하나에 높은 비중을 둘수록 다른 하나의 비중은 낮아진다.
3.4 precision, recall trade-off
이 반비례 관계를 좀 더 이해해보기 위해 SGDClassifier에서 지원하는 decision_function메소드를 활용해보자.
decision_function메소드는 precision을 이용해 임계값을 찾고, 이 임계값을 기준으로 예측했을 때 recall이 어느 정도인지에 따라 점수를 반환한다.
이를 이용해서 어느 정도의 임계값을 가지고 만들지 결정할 수 있다.
y_scores = sgd_clf.decision_function([some_digit])
y_scores
threshold=0
y_some_digit_pred=(y_scores>threshold)
y_some_digit_pred우선 아까 그 0번 '5'를 넣어서 2164.22030239라는 임계값을 얻었다.
그리고 우리가 설정해줄 임계값인 threshold에 0을 넣으면 True로 반환되어, 높은 재현율을 보인다.
반면 임계값을 3000으로 넣었을때는 재현율이 도리어 낮아졌다.
이걸 60000개를 일일이 하고 있으면 다른 일을 못하니까 이것도 자동으로 적절한 threshold 찾는 코드가 있다.
y_scores=cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
plt.plot(thresholds, precisions[:-1], "b--", label="정밀도", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="재현율", linewidth=2)
plt.vlines(threshold, 0, 1.0, "k", "dotted", label="임곗값")
plt.show()일단 아까처럼 예측 결과를 만들어주고, precision을 0부터 1까지(그러면 recall은 1부터 0까지 돌아가게 된다)돌려주는 precision_recall_curve를 이용해 임계값들을 뽑아낸다.
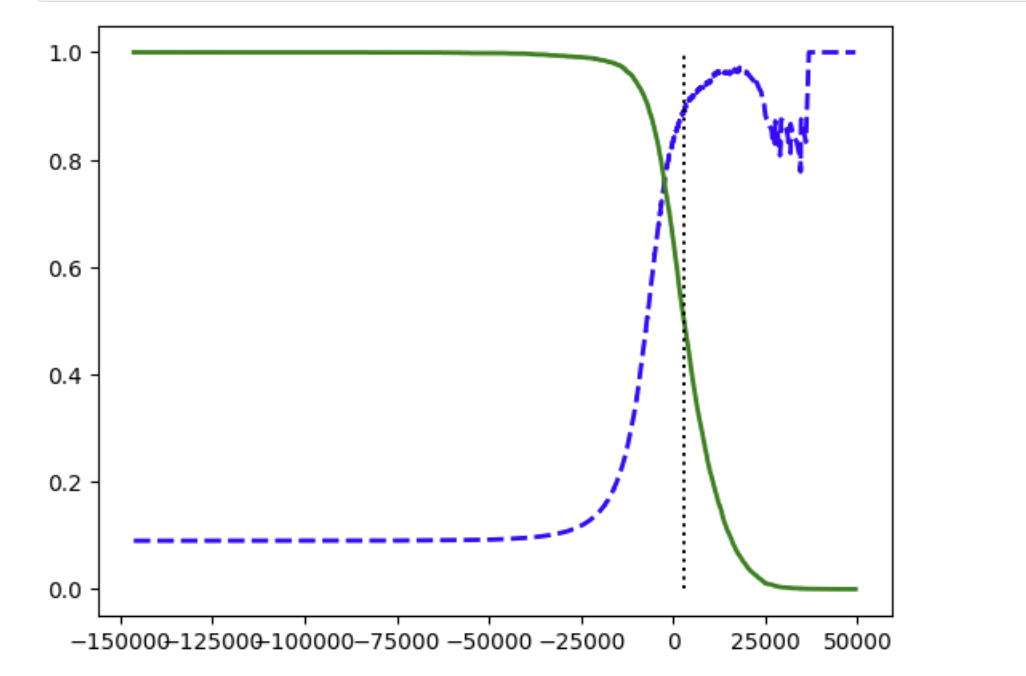
그리고 그걸로 그래프를 그리면 이렇게 나온다.
파랑이 precision, 초록이 recall. 저 점선은 3000이다.
X축이 threshold.
3.5 ROC curve
아까는 precision과 recall이었다면 이번에는 recall은 그대로 쓰고 FPR이라는 개념을 쓴다.
FPR은 5라고 예측한 5아닌것 / 잘못 예측한것 총합.
여튼 이것도 그래프를 그리면 이렇다.
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
idx_for_threshold_at_90 = (thresholds <= threshold_for_90_precision).argmax()
tpr_90, fpr_90 = tpr[idx_for_threshold_at_90], fpr[idx_for_threshold_at_90]
plt.plot(fpr, tpr, linewidth=2, label="ROC curve")
plt.plot([0, 1], [0, 1], 'k:', label="랜덤 분류기의 ROC")
plt.plot([fpr_90], [tpr_90], "ko", label="90%정밀도에 대한 임계값")
plt.show()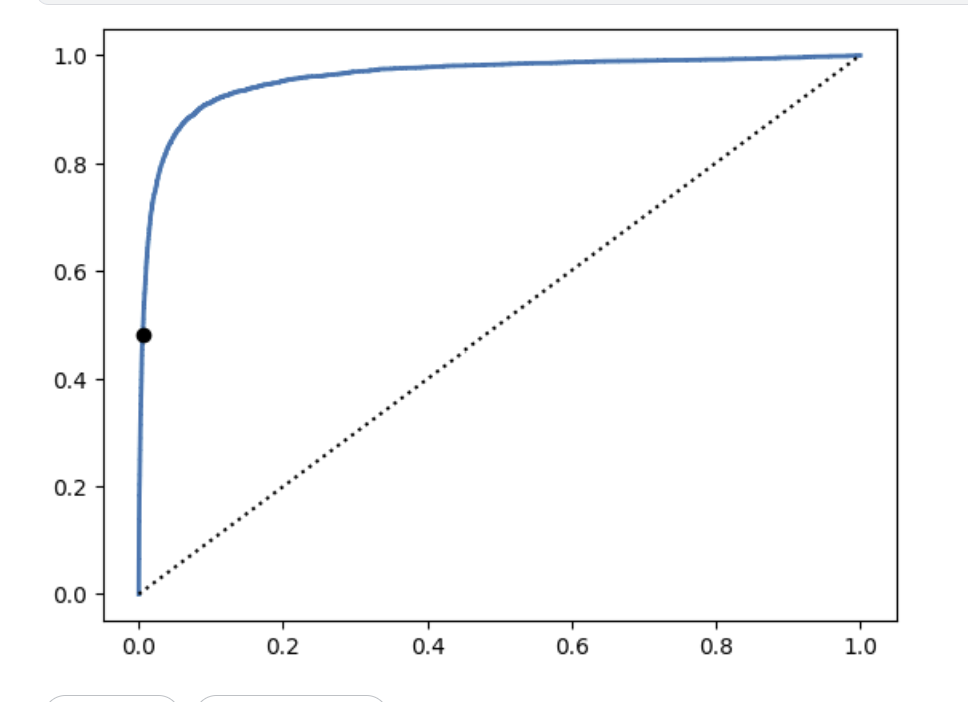
저 점은 precision이 90%인 하한선. 아까 precision, recall 2개가 반비례였던것과 달리 recall과 FPR은 비례다.
4. 다중 분류
크게 OvO 방식과 OvR 방식으로 나뉜다.
먼저 OvO 방식.
from sklearn.svm import SVC
svm_clf = SVC(random_state=42)
svm_clf.fit(X_train[:2000], y_train[:2000])
svm_clf.predict([some_digit])
some_digit_scores = svm_clf.decision_function([some_digit])
some_digit_scores.round(2)
class_id = some_digit_scores.argmax()
class_idOvO 코드. 5를 잘 예측한다.
간단히 말하자면, 2개씩 묶어서 나오는 가능한 모든 조합을 계산하고 거기서 가장 많이 이긴 클래스로 최종 예측한다.
from sklearn.multiclass import OneVsRestClassifier
ovr_clf = OneVsRestClassifier(SVC(random_state=42))
ovr_clf.fit(X_train[:2000], y_train[:2000])
ovr_clf.predict([some_digit])
len(ovr_clf.estimators_)
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
sgd_clf.decision_function([some_digit]).round()OvR 코드. 이쪽은 3과 5가 강하게 예측된다.
이쪽 방식은 아까와는 반대로 10개를 동시에 돌려서 그 중 가장 높게 나온 점수를 예측한다.
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype("float64"))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")별건 아니고, 스케일러를 돌린 뒤 다시 성능을 측정해봤더니 array([0.8983, 0.891 , 0.9018])라는 값이 나오면서 90% 언저리 성능을 보여줬다.
다만, 이건 돌아가는 시간 자체가 오래 걸린다.
5. 오류 분석
from sklearn.metrics import ConfusionMatrixDisplay
y_train_pred=cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
ConfusionMatrixDisplay.from_predictions(y_train, y_train_pred)
plt.show()아까 말한 Confusion Matrix를 이런 식으로 시각화할 수 있다.
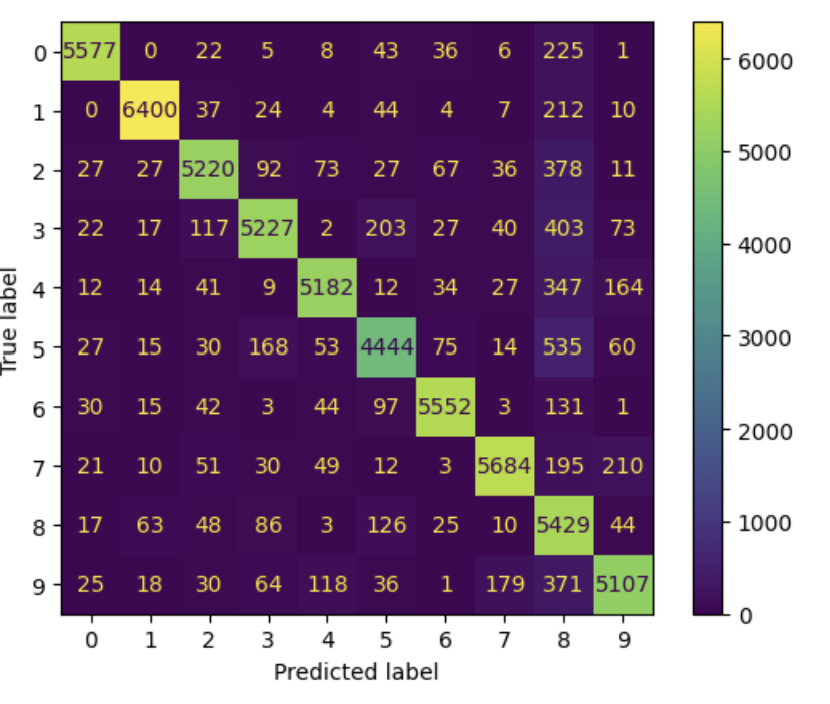
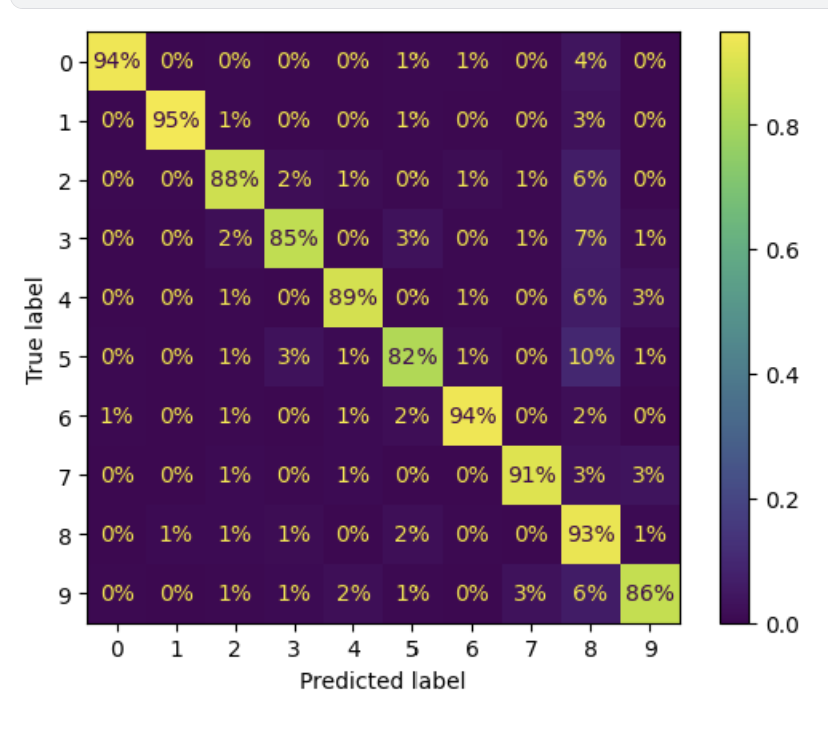
아래건 %로 나타낸 버전.