[AIM5056_41 ML with Graphs] Lec2 Node Embedding

Challenges of ML with Graph

• high computational complexity
• low parallelizability
• Inapplicability of machine learning methods: limited methods with adjacency matrices

Network representation learning

basics

• node embedding $\approx$ network embedding
• instead of feature engineering, use representations and then ML/DL whatever
• Need to Find Representations: learning objective of this lecture

Notations

• input: $G = (V, E, A)$
• output: $Z \in R^{|V| \times k}$, each vector (node representation) with $k$-dimension

DeepWalk

• input: word $\rightarrow$ node
• output: sequence of words $\rightarrow$ random walk
• 1 stance of random walk $\approx$ a sequence of node
• DeepWalk: sequence (walk) 내에서 $v_i$ node를 word로 치환하면 쉬움
• Hyperparameter
  • window size $w$: 주변 몇 개의 node를 볼 것인지?
  • embedding size $d$: 비례 있지만, 둔화됨
  • walks per vertex $\gamma$: 커진다고 항상 더 나아지는 것 아님
    
    
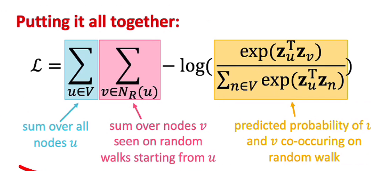
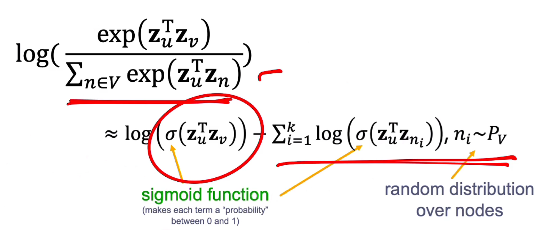
• negative sampling
  • path에 있는 node들은 positive sample이고 나머지는 모두 negative sample
  • complexity: $O(|V|)$ vs hierarchical softmax: $O(|V|log|V|)$
  • how to define $k$?: by degree distribution

Node2Vec

• biased 2nd-order random walk
• local view (BFS처럼, 주변 node가 더 중요할수도) or global view (DFS처럼)?
• parameter: random walk strategy를 결정
  • $p$: previous node로 돌아가는 확률
  • $q$: outwards (DFS) or inwards (BFS)

Graph in to Latent Space

• Encoder
• Measure for Similarity check
  • 연결되었는지, neighbor share하는지, similar structural role인지 etc.

번외: edge representation

• node representation 을 절반으로 나누거나, L1, L2