[AIM5056_41 ML with Graphs] Lec1 Graph Basics

Basics

Components

• Components: nodes & vertices $N\space or \space V$
• Interactions: links & edges $L\space or \space E$
• System: Network, Graph $G = (N,L)\space or \space (V, E)$

netowkrs or graphs?

• network: real systems (e.g. www, they rule)
• graph: matehmatical representation of a network (e.g. web graph, social graph)
• two are usually interchangable

insight를 찾아낼 만한 network를 구성해라

Degree, Average Degree & Degree Distribution

Node Degree

• num of links connected to the node
  
  $\rightarrow k_B=4$
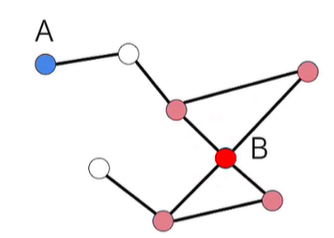
• if directed graph, can be divided into in-degree & out-degree
  
  $\rightarrow k_C^{in}=2$
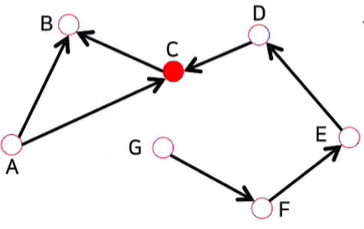
  • Source: $k^{in}=0$
  • Sink: $k^{out}=0$

Average Degree

• undirected graph: $<k> = \frac{1}{N}\sum^{N}_{i=1}$, therefore $<k> = \frac{2L}{N}$
• directed graph: $<k^{in}>=\frac{1}{N}\sum^N_{i=1}k_i^{in}, <k^{out}>=\frac{1}{N}\sum^{N}_{i=1}k_i^{out}, <k^{in}>=<k^{out}>$, therefore $<k> = \frac{L}{N}$

Degree Distribution

• $P(k)$: probability that a randomly chosen node has degree $k$
• degree가 높은 node는 hubs라고 함
• discrete, continuous 있긴 하지만 $\sum p(k) = 1$

Graphs

Adjacency Matrix

• $0$'s in adjacency matrix indicates sparsity & density

Complete Graph

• max num of links a network of N nodes $L_{max} = \frac{N(N-1)}{2}$ & average degree $<k> = N-1$
• 보통의 그래프는 위와 같지 않지만, 어쨌건 $O(|V|) = O(|N|)$

other graphs

• weighted graph: $A_{ij}=w_{ij}$
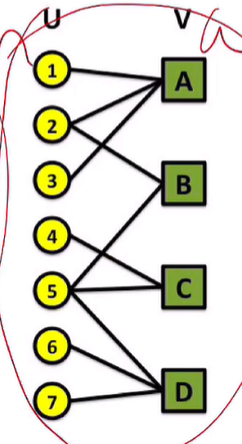
• bipartite graph: nodes can be divided into two disjoint sets $U, V$ s.t. every link connects a node in $U$ to one in $V$
  

Clustering Coefficient

• local clustering coefficient: what fraction of your neighbors are connected? = Node $i$ with degree $k_i$
• global clustering coefficient: # of closed triplets divided by # of all triplets (open and closed)