[논문 리뷰] Collaborative Filtering for Implicit Feedback Datasets 에서 넘어왔습니다.
사용 배경
함수 y=f(x)의 최솟값을 찾는 방법은 여러가지 방법이 있을 수 있다.
만약 f(x)가 이차함수라면 아무 생각없이 f′(k)=0 을 만족하는 k를 찾아서 f(k)가 최소라고 했을 것이다. (최고차항의 계수가 음수인 경우는 그냥 무시하자...) 이렇게 이차함수와 같이 한번의 미분만으로 최솟값을 찾을 수 있는 형태의 함수들을 Convex 하다고 한다. 하지만 f(x)가 사차함수만 되어도 이 방법은 사용이 불가능하다. 일반적으로 사차함수는 f′(k)=0을 만족시키는 k가 3개 존재하고, 단순히 저 정보만 가지고는 그 중 어떤 k가 최소가 되게 하는지 알 수 없다.
현실 세계의 데이터는 당연히 사차함수보다 훨씬 더 복잡한 형태를 가지고 있다. 이러한 이유 때문에 Machine learning에서 Loss function의 최솟값을 구하기 위해 위의 방법을 사용할 수 없고 Gradient descent method를 사용하는 것이다.
그런데 만약, 우리가 최적화하고자 하는 함수가 convex하다면, gradient descent method를 쓰지 않고 그냥 미분해서 0이 되는 지점을 찾아 훨씬 더 쉽게 최적화 할 수 있지 않을까? 라는 아이디어에서 출발한다.
예시
예를 들어 보자
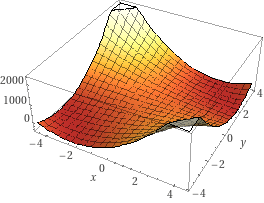
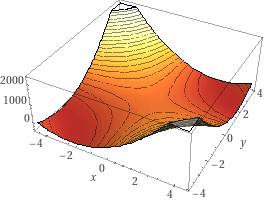
z=5x2y2+2x2+3y2−100xy
위의 z를 최소화 하는 x,y를 찾아보자.
위 식에서 y가 상수라면 x에 대한 이차식으로 생각할 수 있다. 따라서 y가 어떤 값인지는 모르지만, 그 때 최소가 되는 x는 쉽게 구할 수 있을 것이다.
0=∂x∂z=(10y2+4)x−100y x=10y2+4100y⋯(1)
y에 대해서도 동일하다.
0=∂y∂z=(10x2+6)y−100x y=10x2+6100x⋯(2)
식 (1), (2)를 이용해서 최솟값을 찾아보자. 시점은 그냥 마음대로 (1,−1) 에서 시작한다.
먼저 y를 고정하고 식 (1)을 이용해서 x값을 찾는다.
x=14−100≈−7.14
이 값이 의미하는 바는, y=−1 일 때, x≈−7.14 에서 z가 최소화 된다는 뜻이다. 그런데 y는 당연히 -1이 아니고, 이제 식 (2)를 이용해 주어진 x≈−7.14에 대해 y를 구해보자.
y=10⋅(−7.14)2+6100⋅(−7.14)≈−1.38
다시 한번, x=−7.14 일 때, y≈−1.38 에서 최소를 갖는 것이다. 따라서 이 y의 값을 이용해서 x를 다시 구하고, 또 y를 구하고를 반복하면 z를 최소로 하는 x,y를 구할 수 있을 것이다. 아래 python 코드를 활용하여 해당 과정을 반복해보았다.
def cal_z(x, y):
return 5 * x**2 * y**2 + 2 * x**2 + 3 * y**2 - 100 * x * y
def cal_x(y):
return (100 * y) / (10 * (y**2) + 4)
def cal_y(x):
return (100 * x) / (10 * (x**2) + 6)
cnt = 0
x, y = 1, -1
while cnt < 30:
print(cnt, x, y, cal_z(x,y))
x = cal_x(y)
y = cal_y(x)
cnt += 1
| cnt | x | y | z |
|---|
| 0 | 1 | -1 | -392.15 |
| 1 | -7.14 | -1.38 | -420.27 |
| 2 | -5.98 | -1.65 | -433.44 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 29 | -3.42 | -2.78 | -452.21 |
cnt = 29 일 때, z 값은 −452.21 로 계산되었다.
이러한 방식으로 x,y를 고정시키며 번갈아가며 최적화 하는 방법을 Alternating Least Squares 라고 한다.
Wolfram alpha로 그래프를 그려보니 아래와 같이 나왔고, 대략 (−3.41284,−2.78657) 에서 −452.21의 최솟값을 갖는다고 한다.
논문 수식 유도
아래 식에 있는 문자에 대한 의미가 궁금하시면 링크를 참조해주세요.
u,i∑cui(pui−xuTyi)2+λ(u∑∥xu∥2+i∑∥yi∥2)⋯(3)
우리는 위의 식 (3)을 최소화 하는 xu,yi들을 찾는것이 목표다. 식을 잘 보면 x,y가 서로 곱해진 상태로 제곱이 되어있기 때문에, 함수의 형태가 convex함을 보장할 수 없다. 그러나 yi가 상수라고 생각하면, xu에 대한 이차식이고, xu가 상수라고 생각하면 yi에 대한 이차식이 된다. cui,λ는 항상 양수이기 때문에, 해당 식은 convex하게 된다. 이제 위의 예시에서 본 방법을 이용하여 xu,yi를 구해보자.
X : xu를 쌓아서 만든 m×f matrix
Y : yi를 쌓아서 만든 n×f matrix
Cu : Ciiu=cui 인 diagonal n×n matrix
Ci : Cuui=cui 인 diagonal m×m matrix
p(u) : user u에 대해 pui를 나열해놓은 Rn차원의 벡터
p(i) : item i에 대해 pui를 나열해놓은 Rm차원의 벡터
라고 하면,
xu=(YTCuY+λI)−1YTCup(u) yi=(XTCiX+λI)−1XTCip(i)
를 얻을 수 있다. 이제 시작해보자.
먼저 cui(pui−xuTyi)2 부터 처리해본다.
xuTyi cui(pui−xuTyi)2=xu1yi1+xu2yi2+⋯+xuf+yif=cui(pui−(xu1yi1+xu2yi2+⋯+xuf+yif))2
xu=[xu1,xu2,⋯,xuf]T 임을 유의하자. 따라서 scalar 값인 cui(pui−xuTyi)2 를 xu로 미분하면 마찬가지로 f차원의 벡터가 나와야 한다.
∂xu∂cui(pui−xuTyi)2=[∂xu1∂cui(pui−xuTyi)2,⋯,∂xuf∂cui(pui−xuTyi)2]T=[2cui(pui−xuTyi)(−yi1),⋯,2cui(pui−xuTyi)(−yif)]T=−2cui(pui−xuTyi)yi(4)
다음은 λ(∑u∥xu∥2+∑i∥yi∥2) 을 처리해보자.
∥xu∥2=xu12+xu22+⋯+xuf2
어차피 xu에 대해서 미분 할 것이기 때문에 다른 유저나, 아이템들은 상수 취급할 수 있다.
∂xu∂λ(u∑∥xu∥2+i∑∥yi∥2)=2λ[xu1,xu2,⋯,xuf]T=2λxu(5)
식 (3)을 식 (4), (5) 를 이용하면 xu에 대해 미분할 수 있다.
0=∂xu∂(u,i∑cui(pui−xuTyi)2+λ(u∑∥xu∥2+i∑∥yi∥2))=i∑∂xu∂cui(pui−xuTyi)2+∂xu∂λ(u∑∥xu∥2+i∑∥yi∥2)=i∑−2cui(pui−xuTyi)yi+2λxu
1-2 줄 사이에서 xu에 대한 미분이므로 ∑u,i에서 u에 대한 항을 날릴 수 있었다. 식을 조금 정리해보자.
0λxu=i∑−2cui(pui−xuTyi)yi+2λxu=i∑cui(pui−xuTyi)yi=i∑(cuipuiyi−cuixuTyiyi)
xuTyi는 scalar 이므로 xuTyi=yiTxu가 성립한다. 또한 scalar이므로 곱셈의 순서를 바꿀 수 있다. 이를 이용하면
λxu=i∑(cuipuiyi−cuixuTyiyi)=i∑(cuipuiyi−cuiyixuTyi)=i∑(cuipuiyi−cuiyiyiTxu)=i∑cuipuiyi−(i∑cuiyiyiT)xu
∴(i∑cuiyiyiT+λI)xu=i∑cuipuiyi(6)
이제 위 방정식을 만족하는 xu를 구하면 된다.
∑icuipuiyi 를 먼저 보자.
i∑cuipuiyi=cu1pu1y1+cu2pu2y2+⋯+cunpunyn(7)
Y : yi를 쌓아서 만든 n×f matrix
Cu : Ciiu=cui 인 diagonal n×n matrix
p(u) : user u에 대해 pui를 나열해놓은 Rn차원의 벡터
라고 위에서 약속했다. 이해를 위해 수식을 써보면 아래와 같다.
Y=⎣⎢⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡y11y21⋮yn1y12y22⋮yn2⋯⋯⋱⋯y1fy2f⋮ynf⎦⎥⎥⎥⎥⎤
Cu=⎣⎢⎢⎢⎢⎡cu10⋮00cu2⋮0⋯⋯⋱⋯00⋮cun⎦⎥⎥⎥⎥⎤
p(u)=[pu1pu2⋯pun]T
이를 이용해서 식 (7)을 다시 쓸 수 있다.
먼저 Cup(u)를 계산하면 다음과 같은 n×1 행렬을 얻을 수 있다.
Cup(u)=⎣⎢⎢⎢⎢⎡cu1pu1cu2pu2⋮cunpun⎦⎥⎥⎥⎥⎤
이를 보면 해당 행렬이 식(7)의 yi의 계수와 동일함을 확인할 수 있다.
이제 여기에 YT를 곱해보자. 그럼 아래와 같은 f×1 행렬이 나온다.
YTCup(u)=[y1y2⋯yn]⎣⎢⎢⎢⎢⎡cu1pu1cu2pu2⋮cunpun⎦⎥⎥⎥⎥⎤=[cu1pu1y1+cu2pu2y2+⋯+cunpunyn]
∴ i∑cuipuiyi=YTCup(u)(8)
마지막으로 ∑icuiyiyiT 를 풀어보자. 위와 동일한 Y,Cu,p(u)를 사용한다.
i∑cuiyiyiT=cu1y1y1T+cu2y2y2T+⋯+cunynynT
YTCu 를 계산해보자. 아래와 같은 f×n 행렬을 얻을 수 있다.
YTCu=[y1y2⋯yn]⎣⎢⎢⎢⎢⎡cu10⋮00cu20⋯⋯⋱⋯00⋮cun⎦⎥⎥⎥⎥⎤=[cu1y1cu2y2⋯cunyn]
이제 여기에 Y를 곱해보면 아래와 같다.
YTCuY=[cu1y1cu2y2⋯cunyn]⎣⎢⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎥⎤=[cu1y1y1T+cu2y2y2T+⋯+cunynynT]
∴i∑cuiyiyiT=YTCuY(9)
식 (6), (8), (9)를 이용하면,
(i∑cuiyiyiT+λI)xu(YTCuY+λI)xu=i∑cuipuiyi=YTCup(u)
∴xu=(YTCuY+λI)−1YTCup(u)
마찬가지 방법을 사용하면 yi에 대해서도 계산할 수 있다.
꽤 복잡한 것 같지만 한줄 씩 천천히 읽어보면 충분히 해결할 수 있을 것이다.