[논문 리뷰] Collaborative Filtering for Implicit Feedback Datasets

정준환·2022년 10월 8일

논문리뷰 추천시스템

논문리뷰

목록 보기

2/5

논문의 내용을 이해를 위해 제 마음대로 재구성 하였으며 틀린 내용이 있을 수 있습니다. 발견 시 댓글로 알려주시면 감사하겠습니다.

요약

Implicit feedback datasets인 경우가 대다수인 현재 시장상황에서, 어떻게 하면 빠르게 좋은 추천을 할 수 있을까?

1. Introduction

지난주에 Item-based collaborative filtering recommendation algorithms 에 관한 리뷰를 진행했다.

간략히 요약하면 explicit한 datasets에 Item-based CF를 적용하면 좋다는 내용이다. 근데 나는 유튜브 보고 좋아요 안누른다. 쿠팡에서 뭐 사도 리뷰도 잘 안남기는 편이다. 이게 내가 이상한게 아니라 대부분의 사용자들이 다 이런다. 즉, 이론상으론 몰라도 현실 세계에서 적용하려면 explicit한 data보다는 implicit한 data를 어떻게 해석할지가 매우매우 중요하다는 뜻이다.

이런 implicit data는 아래와 같은 주의할 사항이 몇개 있다.

Negative feedback이 없다.
- 내가 아직 유튜브에서 무슨 영상을 안봤는데, 이게 내가 싫어해서 안봤을 수도 있고, 있는지도 몰라서 안봤을 수도 있다.
- 이를 구분할 수 없으니까 explicit 경우와 달리 0인 경우도 모두 고려해서 생각해야된다. 0인 경우를 제외하면 positive feedback만 남아서 추정을 잘못할 확률이 증가한다.
Inherently noisy
- 그렇다고 숫자가 크다고 해서 좋아한다고 볼 수도 없다.
- 내가 티비로 매주 무한도전을 챙겨본다고해서 내가 무한도전을 좋아한다고 판단할 수 없다. 켜놓고 잘수도 있고...
preference가 아니라 confidence
- 즉, numerical value를 preference가 아니라 confidence로 해석해야 한다.
- 내가 제일 좋아하는 TV 프로그램은 이벤트성으로 한번 열리고 끝났는데 즉당히 좋아하는 TV 프로그램은 매주 해서 챙겨볼 수도 있다.
- 따라서 숫자가 크다고 좋아하는것이 아니라, 숫자가 클 수록 좋아할 확률이 높다고 생각하는것이 맞다.
평가가 힘들다.
- explicit의 경우에는 그냥 MSE같은 방법으로 하면 뚝딱 되는 반면에 implicit의 경우는 딱 봐도 뭔가 평가가 애매모호하다.
- 내 모델이 잘 만들어진건지 확인을 명확히 하기 힘들다.

2. Preliminaries

기호를 좀 정리해보자.
$u, v$ 는 users, $i, j$ 는 items다. user와 item 사이의 관계를 observations, $r_{ui}$ 라고 하자.

이 $r_{ui}$ 값은 여기서는 말 그대로 observations를 의미한다. 이 논문은 TV 프로그램 추천을 실험했는데, 이 경우 $r_{ui}$ 는 user $u$ 가 item (TV 프로그램) $i$ 를 얼마나 시청했는지를 의미한다. 즉, 두번 봤으면 $r_{ui} = 2$ , 반만 보고 중간에 껐으면 $r_{ui} = 0.5$ 다.

3. Previous work

3.1 Neighborhood models

나와 취향이 비슷한 사람이 좋아하는 아이템을 추천하거나(user-based), 내가 샀던 아이템과 비슷한 아이템들을 추천(item-based)한다. 굉장히 직관적이고, 성능도 괜찮게 나온다. 위에서 잠깐 설명했듯이, 자세하게 궁금하면 Item-based collaborative filtering recommendation algorithms 을 참고하자.

3.2 Latent factor models

이 논문에서 차용한 모델은 latent factor model이다.

A = \begin{bmatrix} r_{11} & r_{12} & r_{13} & r_{14} & r_{15} \\ r_{21} & r_{22} & r_{23} & r_{24} & r_{25} \\ r_{31} & r_{32} & r_{33} & r_{34} & r_{35} \end{bmatrix}

이런 $3 \times 5$ matrix가 있다고 하자. matrix는 임의의 숫자 $f$ 에 대해서 $(3 \times f)$ 와 $(f \times 5)$ matrix의 곱으로 나타낼 수 있다. 예를 들어 $f=2$ 라면,

B = \begin{bmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \\ x_{31} & x_{32} \end{bmatrix} , C = \begin{bmatrix} y_{11} & y_{12} & y_{13} & y_{14} & y_{15} \\ y_{21} & y_{22} & y_{23} & y_{24} & y_{25} \\ \end{bmatrix}

에 대해서

A = BC

의 형태로 분해할 수 있다. 우리가 중고등학교때 인수분해 하던 것 처럼, matrix도 인수분해를 하는것인데 이를 matrix factorization 이라고 한다.

$B$ 를 보면 3개의 행을 가지는데, 이는 곧 user의 수와 동일하고, $C$ 의 열의 수인 5는 곧 item의 숫자다. 즉, $B$ 는 각각의 user에 대해 $m$ 개의 user-factor vector $x_u \in \R^f$ 를 가지고 있다고 해석할 수 있고, $C$ 도 마찬가지로 각각의 item들에 대해 $n$ 개의 item-factor vector $y_i\in \R^f$ 를 가지고 있다고 해석이 가능하다.

즉, $f$ 차원의 벡터 $x_u, y_i$ 에 대해서 아래처럼 나타낼 수 있다.

B = \begin{bmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \\ x_{31} & x_{32} \end{bmatrix} = \begin{bmatrix} -\ x_1 \ - \\ -\ x_2 \ - \\ -\ x_3 \ - \end{bmatrix} \\ \ \\ C = \begin{bmatrix} y_{11} & y_{12} & y_{13} & y_{14} & y_{15} \\ y_{21} & y_{22} & y_{23} & y_{24} & y_{25} \\ \end{bmatrix} =\begin{bmatrix} | & | & | & | & | \\ y_1 & y_2 & y_3 & y_4 & y_5 \\ | & | & | & | & | \\ \end{bmatrix}

위에서 각각의 $r_{ui}$ 값은 관측된 데이터이고, 이는 $x_u \in \R^f$ 와 $y_i \in \R^f$ 에 의해 계산할 수 있다. $A=BC$ 를 이용해서 하나만 풀어보자. $r_{23} = x_{21}y_{13} + x_{22}y_{23} = x_2^Ty_3$ 이다. 일반화하면 $r_{ui}=x_u^Ty_i$ 라고 볼 수 있다.

한가지 주의해야 할 사항은 matrix $A$ 는 대부분의 값이 0인 굉장히 sparse한 matrix이고, 이 0의 값들은 $x_u, y_i$ 를 계산하는데 사용되는것이 아니라, 이 factor들을 통해 0의 값들을 예측하고자 하는것이 우리의 목표라는 점이다. 즉, prediction $\hat r_{ui} = x_u^Ty_i$ 이다. 따라서 우리가 하고자 하는것은 아래 식으로 정리된다.

\min_{x_*, y_*} \sum_{r_{ui}\text{ is known}} (r_{ui} - x_u^Ty_i) ^2 + \lambda(\|x_u\|^2 + \|y_i\|^2) \quad \cdots \quad(2)

(식의 번호는 논문의 번호를 따라가 생략된 번호가 있을 수 있습니다.)

위의 식에서 $r_{ui}$ 가 known인 경우에만 고려하는 것을 확인할 수 있다. 제일 뒤에 있는 $\lambda$ term은 regularization의 의미를 갖는다.

4. Our model

이 논문은 위에 언급된 3.2 Latent factor models 을 약간 변형하여 implicit model에 적용한다. explicit model에서 사용하던 $r_{ui}$ 대신 사용 할 값들을 구해봐야 한다. 먼저 $r_{ui}$ 를 이용해 preference를 나타내는 값 $p_{ui}$ 를 아래와 같은 방법을 이용하여 구한다.

p_{ui} = \begin{cases} 1 & r_{ui} > 0 \\ 0 & r_{ui} = 0 \end{cases}

이것만으로 $r_{ui}$ 를 대체하기에는 무리가 있다. 해당 TV 프로그램을 많이 봤을수록 좋아할 확률이 높다는 점을 이용해서 confidence를 나타내는 $c_{ui}$ 를 아래와 같은 방법을 이용하여 계산한다.

c_{ui} = 1 + \alpha r_{ui}

여기서 $\alpha$ 는 하이퍼 파라미터중 하나로, 이 논문에서는 실험적으로 $\alpha=40$ 의 값이 좋다는 것을 찾아냈다. 물론 이 방법 말고도 implicit datasets을 해석하는 다른 좋은 방법이 존재할 수 있다. 아무튼 이 논문은 위의 $p_{ui}, c_{ui}$ 를 이용하여 기존의 식 (2)를 아래처럼 살짝 변형했다.

\min_{x_*, y_*} \sum_{u, i} c_{ui}(p_{ui} - x_u^Ty_i) ^2 + \lambda \left( \sum_u\|x_u\|^2 + \sum_i\|y_i\|^2 \right) \quad \cdots \quad (3)

주목할 점이 있는데, 앞선 explicit에 관한 식 (2) 에서는 $r_{ui}$ 가 0이 아닌 경우에 대해서만 진행했기 때문에 계산량이 적을 수 있지만, 이번 (3)의 경우는 0인 경우도 고려해주어야 한다는 점이다. 이 논문이 나올 당시 일반적인 E-커머스 시장에서 $m \times n$ 의 값은 10억정도는 가뿐히 넘길 값이였고, 저 식을 우리가 일반적으로 사용하는 gradient descent method를 이용하여 최적화하기에는 무리가 있었다. 그래서 해당 논문에서는 alternating-least-squares 를 이용하여 해당 식을 최적화했다.

쉽게 설명하자면 먼저 $y_i$ 를 상수로 고정한다. 그러면 식 (3)은 $x_u$ 에 관한 2차식으로 바라볼 수 있다. 원래 식 (3)은 convex함을 보장할 수 없기 때문에 최소가 되게 하는 $x_u, y_i$ 를 gradient descent등의 방법으로 계산했지만, 2차식은 그렇게 할 필요가 없다. 단순히 한번 미분해서 0이 되는 지점을 찾으면 그것이 최소가 되는 지점이다.

따라서 $y_i$ 가 상수라고 가정하고 $x_u$ 에 대하여 미분하여 0이되는 $x_u$ 값을 찾는다. 단, 이 $x_u$ 는 주어진 $y_i$ 에 대해 최소가 되게 하는 지점이므로, 이번에는 $x_u$ 를 고정하고 마찬가지 방법으로 $y_i$ 를 찾는다. 해당 방법을 반복하게 된다면 적절한 지점을 찾아낼 수 있을것이다. 이 논문에서는 보통 10번정도 반복하면 된다고 한다.

자세한 수식 및 예시는 Alternating Least Squares (ALS) 의 예시와 논문 수식 유도 에 포스팅해두었다. 해당 과정을 반복하면 각각의 과정에서 아래와 같은 식을 얻을 수 있다.

x_u = (Y^TC^uY + \lambda I)^{-1}Y^TC^up(u) \quad \cdots \quad (4) \\ \ \\ y_i = (X^TC^iX + \lambda I)^{-1}X^TC^ip(i) \quad \cdots \quad (5)

$X$ : $x_u$ 를 쌓아서 만든 $m \times f$ matrix
$Y$ : $y_i$ 를 쌓아서 만든 $n \times f$ matrix

$C^u$ : $C^u_{ii} = c_{ui}$ 인 diagonal $n \times n$ matrix
$C^i$ : $C^i_{uu} = c_{ui}$ 인 diagonal $m \times m$ matrix

$p(u)$ : user $u$ 에 대해 $p_{ui}$ 를 나열해놓은 $\R^n$ 차원의 벡터
$p(i)$ : item $i$ 에 대해 $p_{ui}$ 를 나열해놓은 $\R^m$ 차원의 벡터

이 방법을 이용하면 최적화의 모든 과정이 data size의 상수배 시간안에 해결된다. 이렇게 $x_u, y_i$ 를 얻었으면 $\hat p_{ui} = x^T_u y_i$ 를 계산해서 높은 값을 갖는 아이템을 추천해주면 된다. 이게 전부다. 논문에서는 이 전반적인 과정에서 핵심적으로 딱 두가지를 강조하고 있다.

$r_{ui}$ 값을 이용해서 $p_{ui}, c_{ui}$ 를 도출해내고, 이를 이용해 식을 계산했다. 물론 $p_{ui}$ 를 계산하는 과정에서 기준을 0으로 두는것이 아닌 어떤 다른 threshold를 줘도 좋고, $c_{ui}$ 에서도 다른 식을 사용할 수도 있다. 하지만 중요한점은, 아무튼 $r_{ui}$ 를 직접 사용하는것이 아니라, 나누어 주어야 예측 결과가 훨씬 좋게 나온다. (후에 실험적으로 보인다.)
alternating least squares를 사용해서 계산을 linear 시간 안에 해결할 수 있다.

5. Explaining recommendations

사실 수식적으로 받아들일 순 있어도 이해는 잘 안되는게 당연하다. Neighborhood-based 모델에서는 설명이 굉장히 직관적이고, 바로 이해가 된다. 그런데 우리의 model에서도 그런가? 결과적으로 추천이 잘 된다 하더라도, 왜 추천이 잘 되는지를 알아보자.

식 (4)를 이용해서 $\hat p_{ui}$ 를 다시 계산해보자.

\begin{aligned} \hat p_{ui} &= x_u^T y_i \\ &= y_i^Tx_u \\ &= y_i^T (Y^TC^uY + \lambda I)^{-1}Y^TC^up(u) \\ &= y_i^T W^u Y^TC^up(u) \\ \end{aligned}

$W^u = (Y^TC^uY + \lambda I)^{-1}$ 라고 하면 위처럼 정리할 수 있다. $Y$ 가 의미하는 바는 아이템들의 정보, $C^u$ 가 의미하는 바는 user $u$ 에 대한 각각의 아이템들의 confidence다. 따라서 $W^u$ 는 user $u$ 에 대한 weighting matrix라고 이해할 수 있다. 그렇다면 $u$ 에 대해 아이템 $i, j$ 의 weighted similarity $s^u_{ij}$ 도 $s^u_{ij} = y_i^T W^u y_j$ 라고 나타내는것이 받아들이기 어렵지 않다. 왜 이렇게 써보냐면 이렇게 하면 위의 식이 아래처럼 깔끔하게 정리된다.

\hat p_{ui} = \sum_{j:r_{ui}>0} s^u_{ij}c_{uj} \quad \cdots \quad (7)

주의할점은, $p(u)$ 의 계산을 위해 $r_{ui}$ 가 0보다 큰 $j$ 에 대해서만 고려해야 한다는 점이다. 뭐 계산을 하고자 나타낸것은 아니고, 식 (7)를 보면 이제는 우리가 latent factor model이 추천을 왜 잘 할수 있는지 이해할 수 있다.

(정확한 수치가 아님을 유의하자. 단순히 직관적인 이해를 위해서다.)
먼저 $c_{uj}$ 는 $u$ 가 $j$ 를 얼마나 좋아하냐를 보여준다. 거기에 $i, j$ 가 얼마나 비슷한 아이템인지를 보여주는 $s^u_{ij}$ 를 곱해서 다 더해주면, 이것이 곧 $u$ 가 $i$ 를 얼마나 좋아할지를 보일 수 있는 것이다. 심지어, 기존의 neighborhood-based와 다르게 아이템의 유사도 계산이 유저에 따라서 달라진다.

예를 들어, 나는 무한도전이랑 1박2일이 비슷하다고 생각하는데, 세상에 다른 누군가는 그렇게 생각하지 않을 수 있다. 이 경우 neighborhood-based는 정확한 추천이 힘들 수 있지만, 이 모델은 가능하다.

6. Experimental study

이제 우리는 우리의 모델이 왜 추천을 잘 할 수 있는지 직관적으로 이해도 했고, 수식적으로 나타낼 수도 있다. 이제 진짜 맞는지 실험을 해보자.

Data description

30만개의 셋탑박스에서 4주간 수집한 데이터를 $r_{ui}$ : training set, 그 뒤의 한주를 $r^t_{ui}$ : test set으로 했다. 채널은 약 17000개 정도 확인됐다고 하고, non-zero $r_{ui}$ 는 약 320만개다. $u$ 는 30만, $i$ 는 17000이니까 매우매우 sparse함을 알 수 있다.

이후, TV 프로그램 데이터에 맞게 전처리를 잔뜩 해주는데, 흐름에 크게 중요하지 않으니까 넘어간다.

Evaluation methodology

그래서 이제 평가는 어떻게 할까?
각각의 유저에 대해서 추천 할 아이템을 정렬해서 쭉 줄을 세운다. 이후 $rank_{ui}$ 를 $u$ 가 $i$ 를 얼마나 앞에다 놔뒀냐를 %로 보이는 값이라고 해보자. 100개의 아이템중에 1등이면 1%, 100등이면 100%가 될 것이다 (낮을수록 좋다). 이제 이 $rank_{ui}$ 를 이용해서 모델 전체의 퀄리티는 아래와 같은 방법을 이용한다.

\overline{rank} = \frac{\sum_{u, i}r^t_{ui}rank_{ui}}{\sum_{u, i}r^t_{ui}}

$rank_{ui}$ 를 $r^t_{ui}$ 를 이용해 weighted-sum 했다고 생각하면 된다. $rank_{ui}$ 값이 작을 때, $r^t_{ui}$ 값은 큰것이 좋다. 따라서 $\overline{rank}$ 값이 낮을수록 추천을 잘 했다고 볼 수 있고, $\overline{rank} \leq 50%$ 이면 그냥 랜덤으로 고른거나 마찬가지라는것도 알 수 있다.

Evaluation results

그냥 인기있는 프로그램 추천 vs item-based CF vs 우리꺼

이렇게 세가지를 비교를 해봤다.

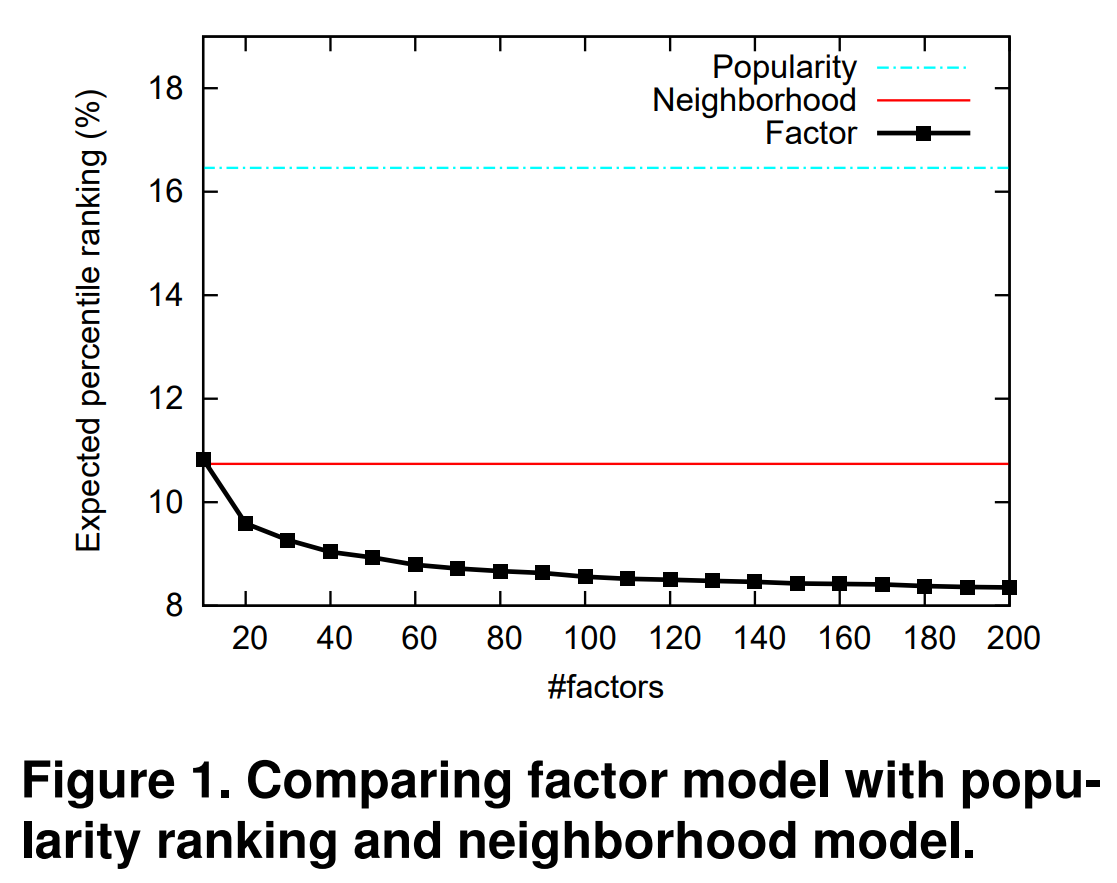
Figure 1을 보면 우리 모델이 제일 좋다는것을 확인할 수 있다. 또한 factors의 수가 커질수록 성능이 점점 더 좋아진다.

식 (2)를 implicit의 특성을 고려하여 $p_{ui}, c_{ui}$ 를 이용해 식 (3)으로 변형한 것에 의문을 가질 수 있어서 그냥 (2)를 가지고도 실험을 해봤는데, 당연히 (3)이 더 좋았다.

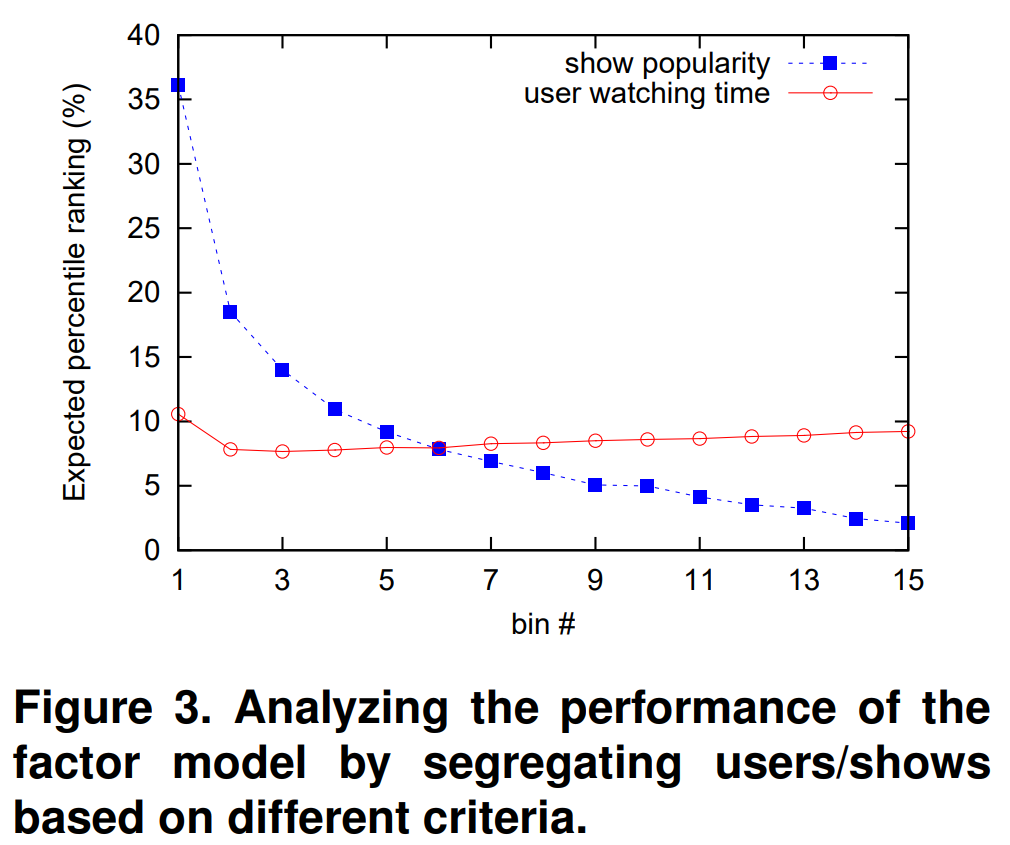
좀 신기한 사실이 있었는데, 먼저 TV 프로그램을 인기순으로 15개의 그룹으로 나눴다. (1이 인기 없고, 15가 인기 있는 순) Figure 3의 파란색 라인을 보면, 인기 없는 프로그램에 대해서는 추천을 너무 못했다는 것을 볼 수 있다. 어떻게 보면 자연스러운것이, 인기있는 TV 프로그램에 대한 데이터가 훨씬 많기 때문이다.

근데 이게 user에 대해서는 통하지 않았다. 이번에는 user를 시청 시간에 따라서 같은 방법으로 15그룹으로 나눴다. Figure 3의 빨간색 라인을 보면, user들의 시청시간은 추천에 그다지 영향을 안미침을 볼수 있다. 논문의 저자는 그냥 사람들이 대부분 비슷한 TV 프로그램을 보기 때문이라고 추측했다.