Confusion Matrix 이해하기

정준환·2022년 12월 18일

1. Confusion Matrix란?

Confusion Matrix는 Classification 문제에 있어서 가장 근간이 되는 Matrix다. 우리가 흔히 알고있는 평가 Metric (Accuracy, Precision, Recall, AUROC 등..)은 모두 이 Confusion Matrix에서 부터 시작한다.

어떤 데이터와 그에 대한 예측 결과가 있다고 하자. 우리는 하나의 Datum에 대해서 나올 수 있는 경우를 크게 4가지로 나누어 볼 수 있다.

TP (True Positive) : 예측을 positive로 했는데, 맞춘 경우
TN (True Negative) : 예측을 negative로 했는데, 맞춘 경우
FP (False Positive) : 예측을 positive로 했는데, 틀린경우
FN (False Negative) : 예측을 negative로 했는데, 틀린경우

표로 나타내보면 아래와 같다.이런 꼴을 Confusion Matrix라고 부른다.

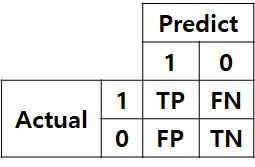
예시

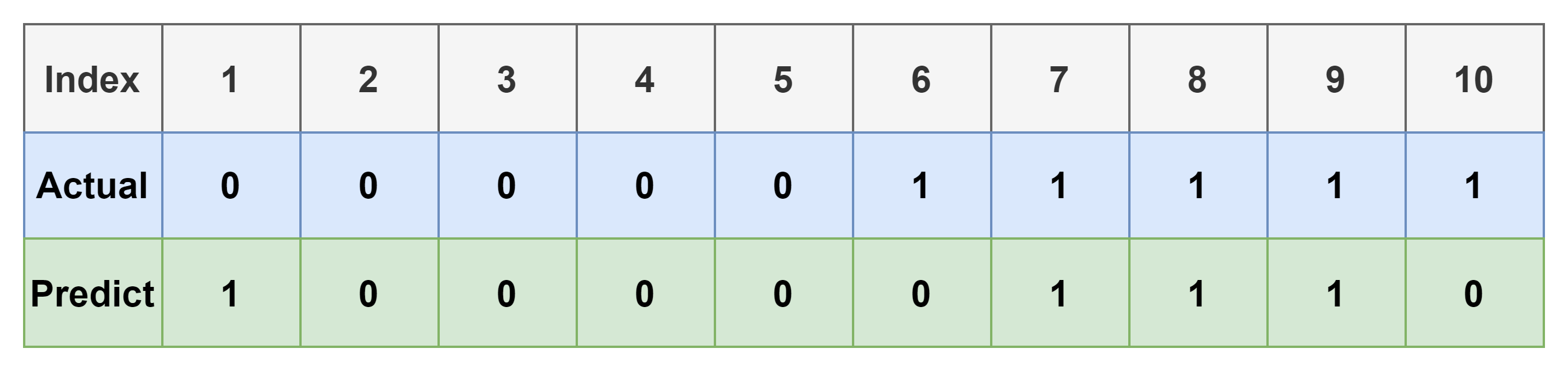
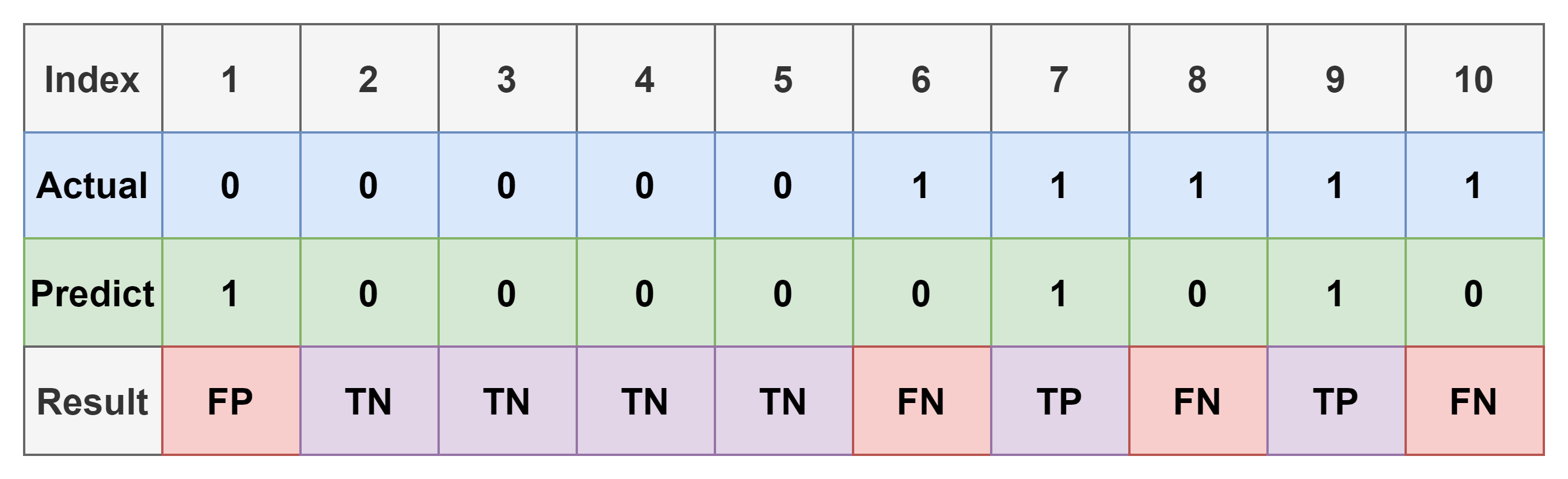
간단한 예시를 들어보자. 아래 표는 10개의 data와 그에 대한 예측 결과를 나타낸다.

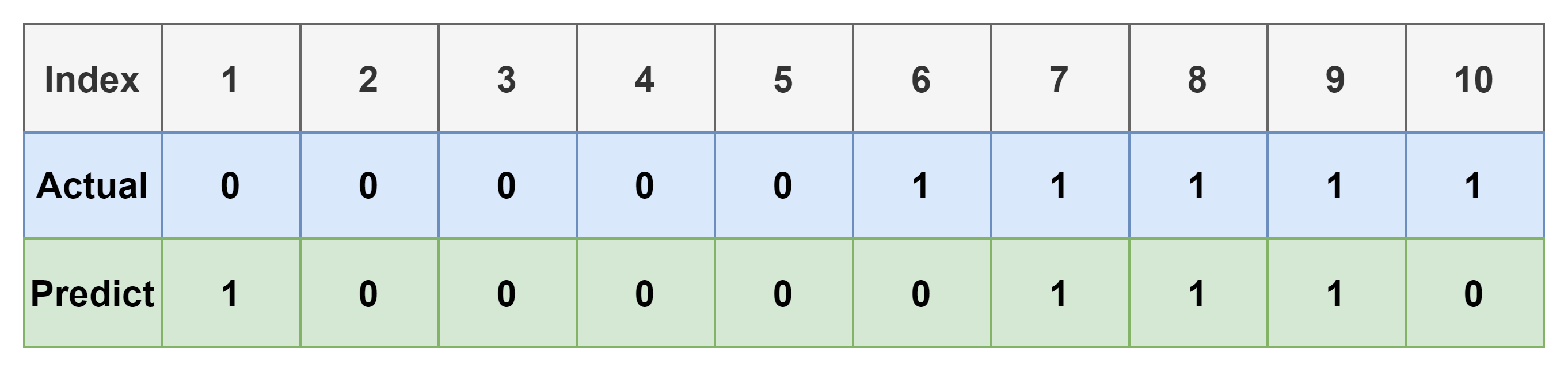
위의 표에서 각 index 대한 결과는 아래와 같다.

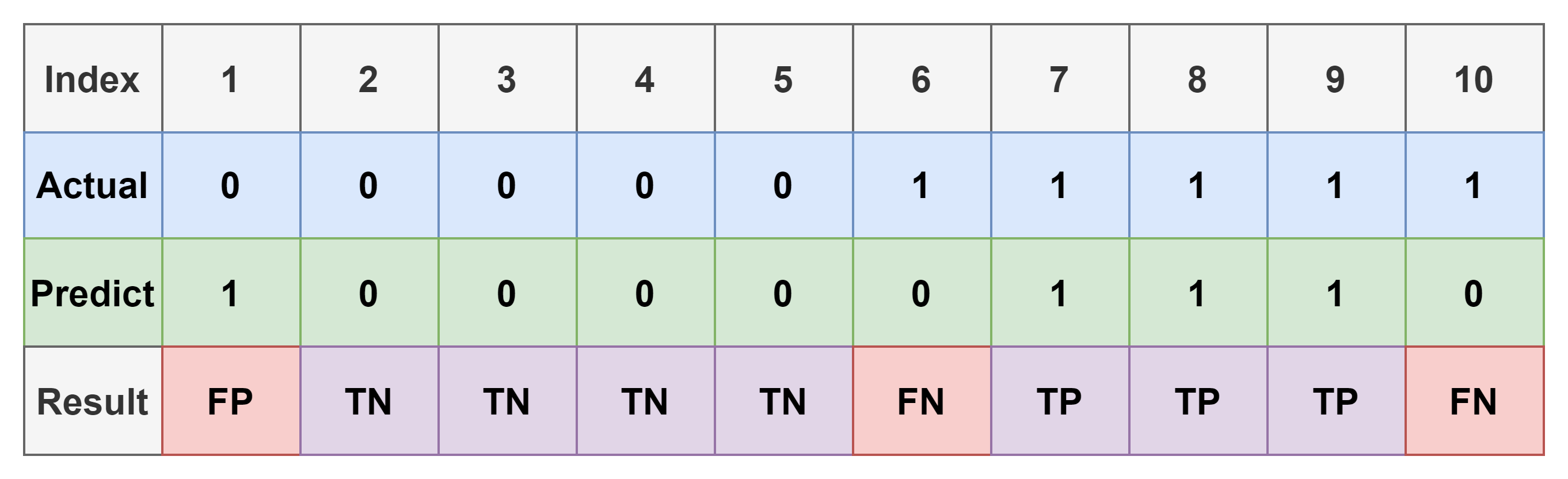
TP: 3개, [7, 8, 9]
TN: 4개, [2, 3, 4, 5]
FP: 1개, [1]
FN: 2개, [6, 10]

그럼 이를 이용하여 Confusion Matrix는 쉽게 만들 수 있다.

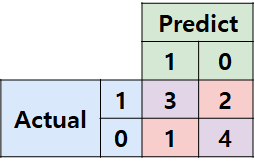
2. Confusion metrics를 이용한 Metric

분류 문제에서 사용할 수 있는 여러가지 Metric을 위의 Confusion Matrix를 이용해 구해보자.

Accuracy

Positive와 Negative를 가리지 않고, 얼마나 정확하게 맞췄는지를 계산하는 지표

Acc = \frac{TP + TN}{TP + TN + FP + FN}

위의 예시에서 계산해보면 아래와 같다.

Acc = \frac{3 + 4}{3 + 4 + 1 + 2} = 0.7

Precision

모델이 Positive라고 예측한 경우(TP + FP)만 고려했을 때, 얼마나 정확한 예측을 했는지에 대한 지표

Precision = \frac{TP}{TP + FP} = \frac{3}{3 + 1} = 0.75

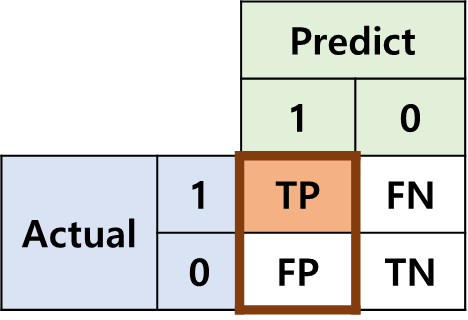
Recall

실제가 Positive인 경우(TP + FN)만 고려했을 때, 얼마나 정확한 예측을 했는지에 대한 지표

Recall = \frac{TP}{TP + FN} = \frac{3}{3 + 2} = 0.6

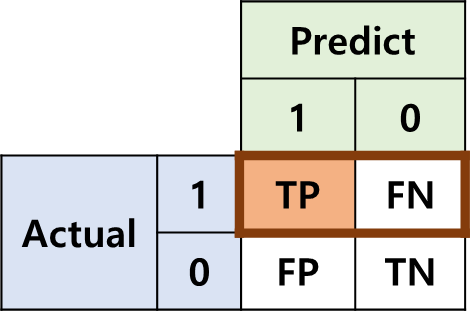
3. 기존 metric의 한계점

Threshold에 크게 영향을 받는다는 단점이 있다. 다시 예시를 가져오자.

실제 우리의 모델은 0, 1로 Binary하게 예측하는 것이 아니다.
Sigmoid등의 함수를 이용하여 아래 표와 같이 0~1 사이의 어떤 실수 값을 가지도록 하는 것이 일반적이다.

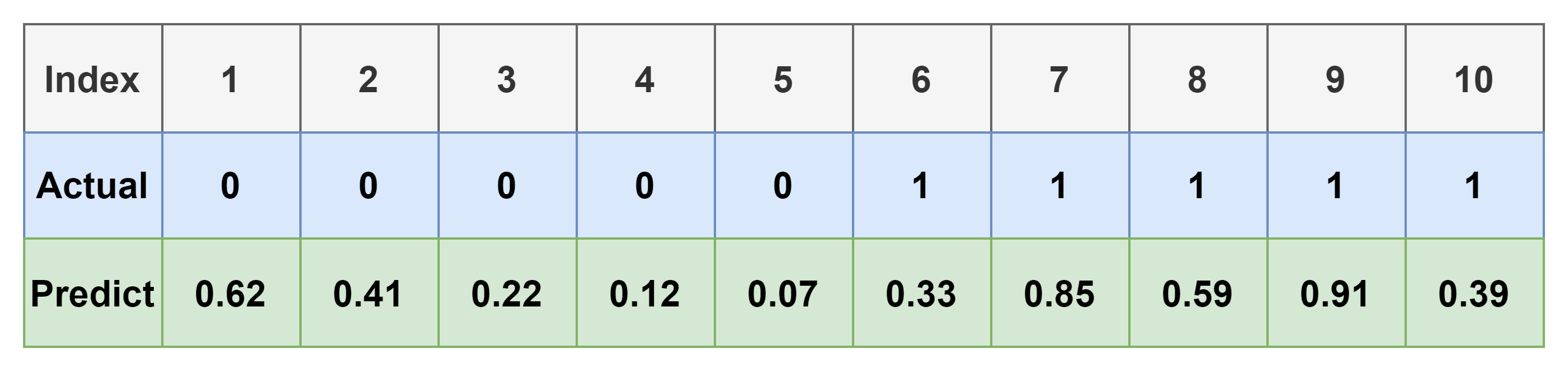
위 표에 0.5의 Threshold를 걸면 우리가 봤던 예시와 동일하다.
근데 0.6을 걸면? 0.7이면? Threshold에 따라 다른 결과가 도출 될 것이다.
예를 들어, threshold가 0.6인 경우에 대한 confusion matrix를 그려보자.

8번 index에 대해 결과가 바꼈고, 1개의 예측 결과가 TP에서 FN이 됐다.

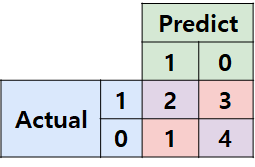
이에 따라 당연히 모델의 예측 결과도 아래처럼 바뀐다.

Precision vs. Recall

앞서 설명한 Precision과 Recall은 Threshold에 따라 서로 반대되는 경향성을 보인다. 아래의 경우를 살펴보자.

Threshold가 굉장히 큰 경우 (0.99인 경우를 생각해보자)
- FP (모델이 잘못된 예측을 한 경우) 가 작을 가능성이 크다. 따라서 precision이 커진다.
- TP는 반대로 작아진다. TP + FN은 고정이다. 따라서 Recall은 작아진다.
Threshold가 굉장히 작은 경우 (0.01인 경우를 생각해보자)
- TP (모델이 옳은 예측을 한 경우) 가 크다. 극단적으로 모든 아이템을 다 1로 예측해버리면 Recall = 1이다.
- FP (모델이 잘못된 예측을 한 경우) 도 마찬가지로 커진다. 따라서 Precision이 작아진다.
이를 대체하기 위해 조화평균을 이용한 F1-Score 라는 것도 존재한다.

F1-Score = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} =\frac{2 \cdot Precision \cdot Recall}{Precision + Recall}

누군가는 이렇게 생각할 수도 있다.

💡 Sigmoid를 씌워서 0~1 사이의 확률 값을 예측 하는 것인데, Threshold는 무조건 0.5(50%)로 설정하는 것이 맞지 않나요?

아니다! 암 환자를 예측하는 경우를 생각해보자.

우리의 예측은 무조건 정확할 수 없다. 아래 두 경우를 살펴보자
1. 어떤 환자가 암이 아닌데, 암으로 예측하는 경우 (1종 오류)
2. 어떤 환자가 암인데, 암이 아니라고 예측하는 경우 (2종 오류)
당연히 2번 case가 훨씬 critical하므로 해당 case를 줄이도록 해야한다. (=Threshold를 잘 설정해야 한다.)
더 알고싶으면 1종 오류, 2종 오류에 대해 검색해보자.