Confusion Matrix를 이용하면 Accuracy, Precision, Recall 등 다양한 Metric을 쉽게 계산할 수 있다. 다만 이들은 모두 Threshold에 영향을 받는다는 단점이 있다.
이러한 단점을 해결한 AUROC, AUC-ROC가 등장한다.
Confusion Matrix가 뭔지 잘 모른다면 Confusion Matrix 이해하기를 읽고 돌아오자.
1. ROC Curve란?
AUROC (Area Under ROC Curve), AUC-ROC (Area Under Curve of ROC Curve) 두개는 똑같은 말이다. 아무튼 ROC curve의 넓이를 의미한다. 그럼 AUROC를 이해하기 위해서는 먼저 ROC가 무엇인지 알아야한다.
ROC는 Receiver Operating Characteristic의 약자로, 이 곡선 자체만으로도 하나의 포스팅이 나와야한다. 다만 이번에는 AUROC에 집중해 필요한 내용만 담았다.
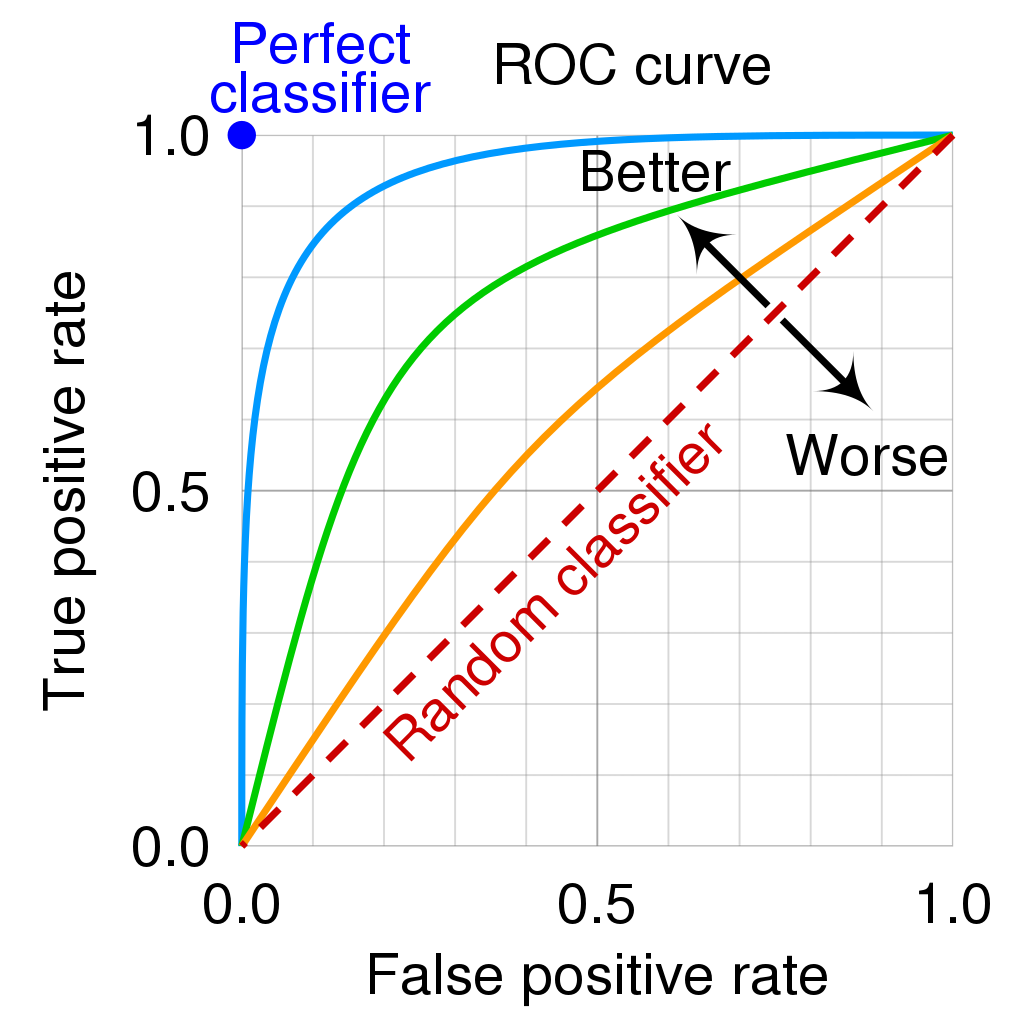
이미지 출처: https://en.wikipedia.org/wiki/Receiver_operating_characteristic
결국은 Curve, 즉 그래프를 그려야하니까 x축과 y축이 무엇인지 살펴보자.
- x축: FPR (False Positive Rate)
- y축: TPR (True Positive Rate)
새로운 용어가 등장했다. 하지만 걱정 할 필요 없다. 모든것은 Confusion Matrix에서 나온다.
혹시 헷갈릴 수 있는 분들을 위해 이전 포스팅의 내용을 복사해왔다.
- TP (True Positive) : 예측을 positive로 했는데, 맞춘 경우
- TN (True Negative): 예측을 negative로 했는데, 맞춘 경우
- FP (False Positive): 예측을 positive로 했는데, 틀린경우
- FN (False Negative): 예측을 negative로 했는데, 틀린경우
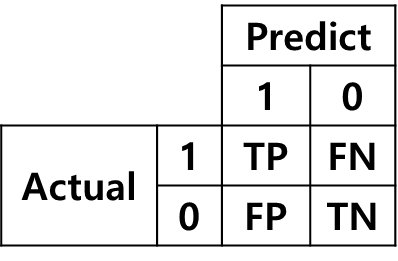
우리는 True Positive와 False Positive가 무엇인지 안다. 그럼 생각을 해보자. 거기에 Rate를 붙이면 뭘까? 하나씩 곱씹어보자.
TPR
직역해버리면 TP가 차지하는 비율. 그럼 분모를 뭘로 잡는게 맞을까.
- 예측 값 전체
- Predict가 True로 인 경우 (= Precision)
- Actual이 True인 경우 (= Recall)
이렇게 3가지 경우 정도를 생각해볼 수 있다. 이 중, TPR은 바로 3번 케이스를 의미한다. 즉, TPR은 사실 Recall과 같다.

FPR
직역해버리면 FP가 차지하는 비율. 마찬가지로 말만 보면 3가지가 가능하다.
- 예측 값 전체
- Predict가 True인 경우
- Actual이 False인 경우
위에서 TPR이 3번 케이스였으니까 얘도 당연히 3번이다. 그냥 이건 약속이다.
이제 우리는 ROC Curve의 x, y축이 무엇인지 알았다. 한번 그려보자! 이전 포스팅의 Confusion Matrix를 가져왔다.
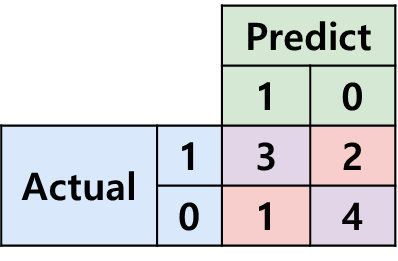
이 Confusion Matrix에서 TPR과 FPN을 계산해보자.
- x축:
- y축:
어라? 선생님 그래프라면서요 이건 그냥 점인데요?
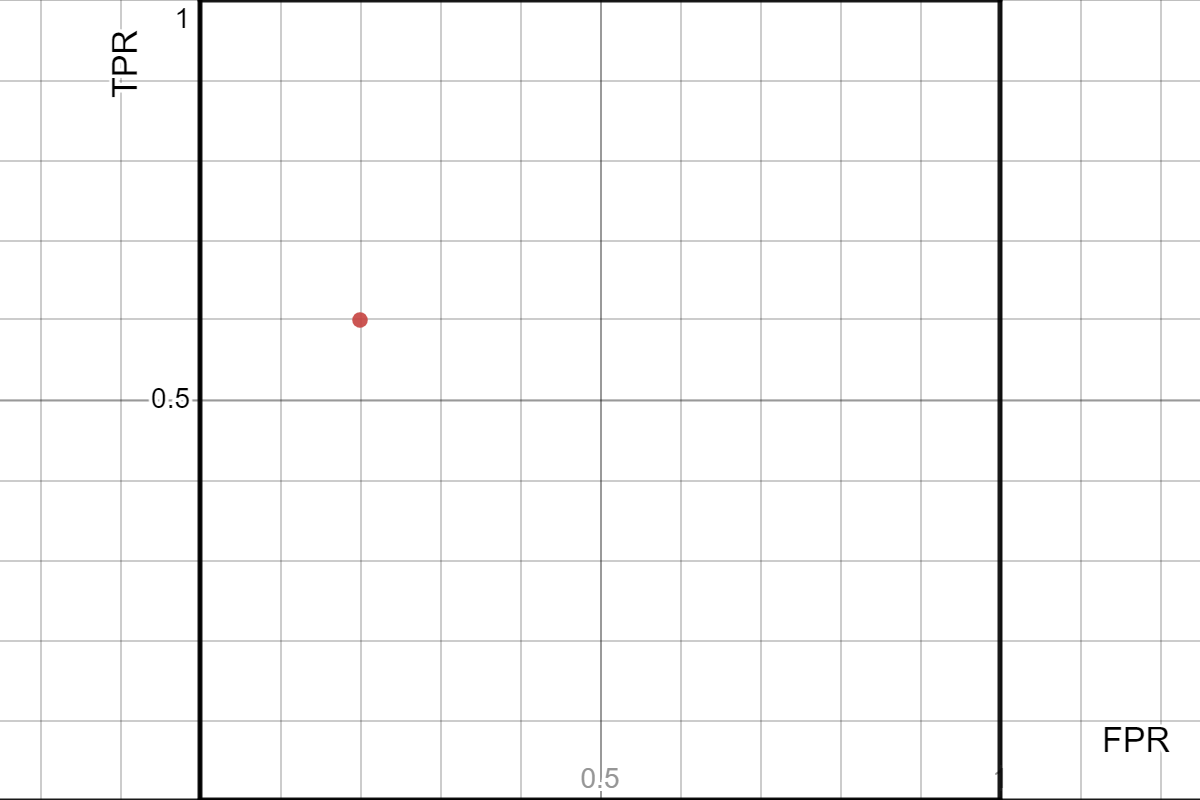
맞다 이건 점이다... 왜냐면 하나의 Confusion Matrix에서는 아무리 뭘 해도 TPR, FPR은 고정된 하나의 값이 나오기 때문이다... 그럼 어떡하지...
2. ROC Curve 그리기 기초
아니 Curve인데 왜 점이 하나만 찍이지? 그래프를 어떻게 그리라는 거야? 처음으로 돌아가서 생각해보자.
Confusion Matrix는 어떤 예측 값에 Threshold에 따라 분류를 진행한 후, 나온 결과다. 위에 든 예시의 경우, 아래의 표에 Threshold를 0.5로 잡았을 때 나온 결과다. (이전 포스팅의 내용이다)

근데 우리는 Threshold에 영향을 받지 않는 Metric을 살펴보고자 지금 ROC Curve를 그려보고 싶은 것 아닌가? 앞뒤가 맞지 않는다. Confusion Matrix를 그린다는 것 자체가 이미 Threshold를 설정해야만 가능한 것인데, 어쩌라고?
해결 방법은 간단하다. Threshold는 0~1 사이의 실수니까 그냥 모든 경우에 대해 Confusion Matrix를 만들고, 그 점들을 싹 다 찍어버리면 된다.
하지만 실제로는 0~1 사이의 실수는 무한하므로 그걸 다 찍어볼 수는 없다. 예시를 보면서 설명하겠다.
위의 표에서 Threshold가 0.1 단위로 떨어진 경우의 Confusion Matrix를 그려봤다.

그리고 각 경우에 대한 FPR, TPR을 계산했다.

드디어 점이 좀 생겼다. 이 점들을 다시 한번 찍어보자.
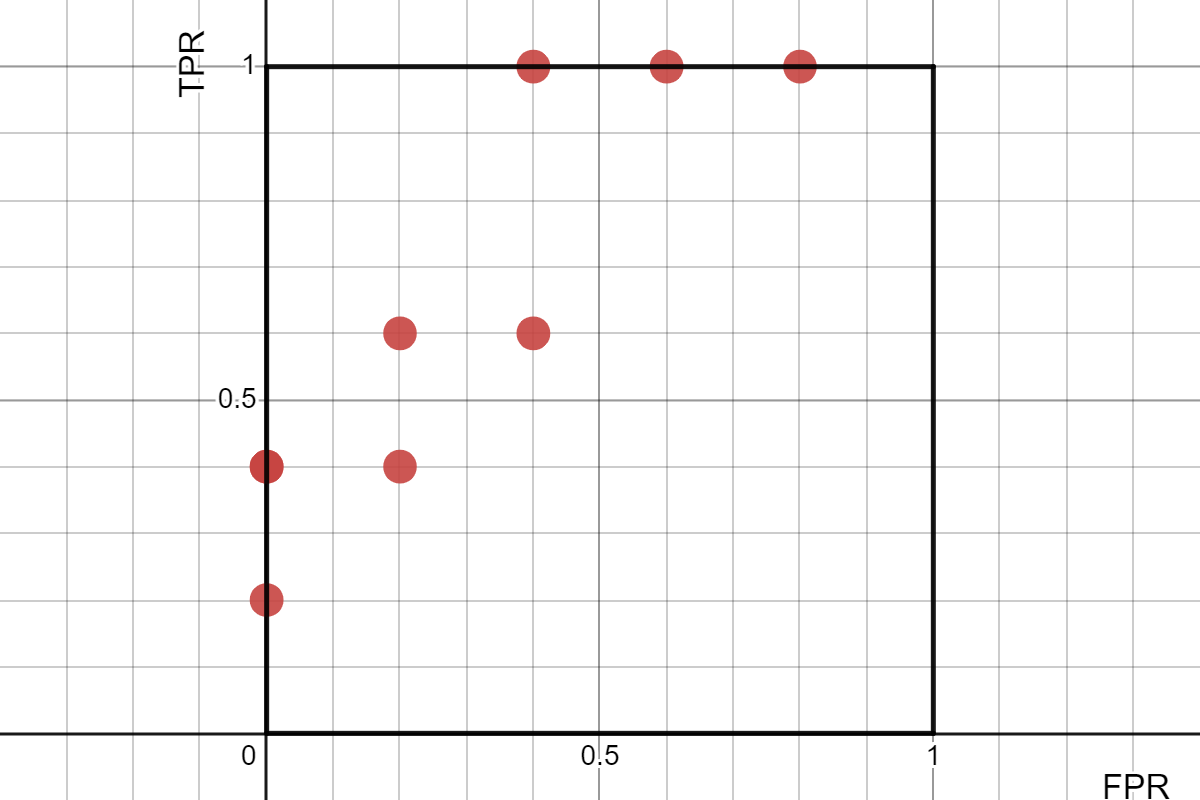
이제야 뭔가 우리 눈에 익숙한 그래프가 그려지기 시작한다. 조금만 더 생각해보자.
-
Threshold가 0.7인 경우와 0.8인 경우, FPR, TPR이 모두 일치해 같은 점이 찍힌다. 즉, 찍을 필요 없는 점을 한번 더 찍은 셈이다. 왜냐면 0.7~0.8 사이의 예측 값을 갖는 경우가 존재하지 않아, 동일한 Confusion Matrix가 만들어졌기 때문이다.
-
반대로 0.3~0.4 사이에는 구분되는 값이 2개 존재한다. (index=6, predict=0.33과 index=10, predict=0.39) 즉, 0.3, 0.4의 Threshold 만으로는 두 경우를 구분할 수 없다는 뜻이다. 0.33~0.39 사이의 어떤 값을 Threshold로 가질 때 Confusion matrix를 그려보고, 그 경우의 FPR, TPR을 찍어야 두 경우를 구분할 수 있다.
1번 케이스를 보면, 우리가 정말 모든 실수에 대해서 Threshold를 설정하고, 그에 따른 Confusion Matrix를 그릴 필요는 없음을 알 수 있다. 적절한 Threshold를 선택해, 그 경우에 대해서만 Confusion Matrix를 그리고, FPR과 TPR을 계산하면 된다.
2번 케이스를 보면, 1번 케이스에서 얘기한 “적절한 Threshold”를 선택하는 방법을 알 수 있다. 바로 우리 모델의 예측 결과의 값들을 이용하는 것이다.
3. 진짜 ROC Curve 그리기
바로 위에서 설명한 방법을 이용해 적절한 Threshold를 잡아보자. 아래 예시를 통해 설명하겠다.

이 표는 이미 위에 한번 나왔던 표다. 범위를 쉽게 잡기 위해, Predict row를 기준으로 정렬했다.

이제 이 표를 보고 아래와 같은 방법으로 값들을 분리할 수 있다.
- 모든 값이 다 True (Threshold = 0)
- 0.07 까지 False (Threshold = 0.07)
- 0.12 까지 False (Threshold = 0.12)
- …
- 0.85 까지 False (Threshold = 0.85)
- 0.91 까지 False (Threshold = 0.91)
- 모든 값이 다 False (Threshold = 1)
물론 0과 1에서 겹치는 점이 나오긴 한데, 그냥 넘어가자. 아무튼 중요한 점은, 우리의 Predict 값들을 Threshold로 사용한다는 점이다. 0~1 사이의 다른 어떤 값을 Threshold로 설정해도, 이 이외의 경우는 존재할 수 없다.
이렇게 하면 아래와 같은 FPR, TPR을 얻을 수 있다. (Confusion matrix는 생략한다)

이제 이 값들을 이용하면 우리의 예측 결과에 대한 ROC Curve를 그릴 수 있다. 짠!
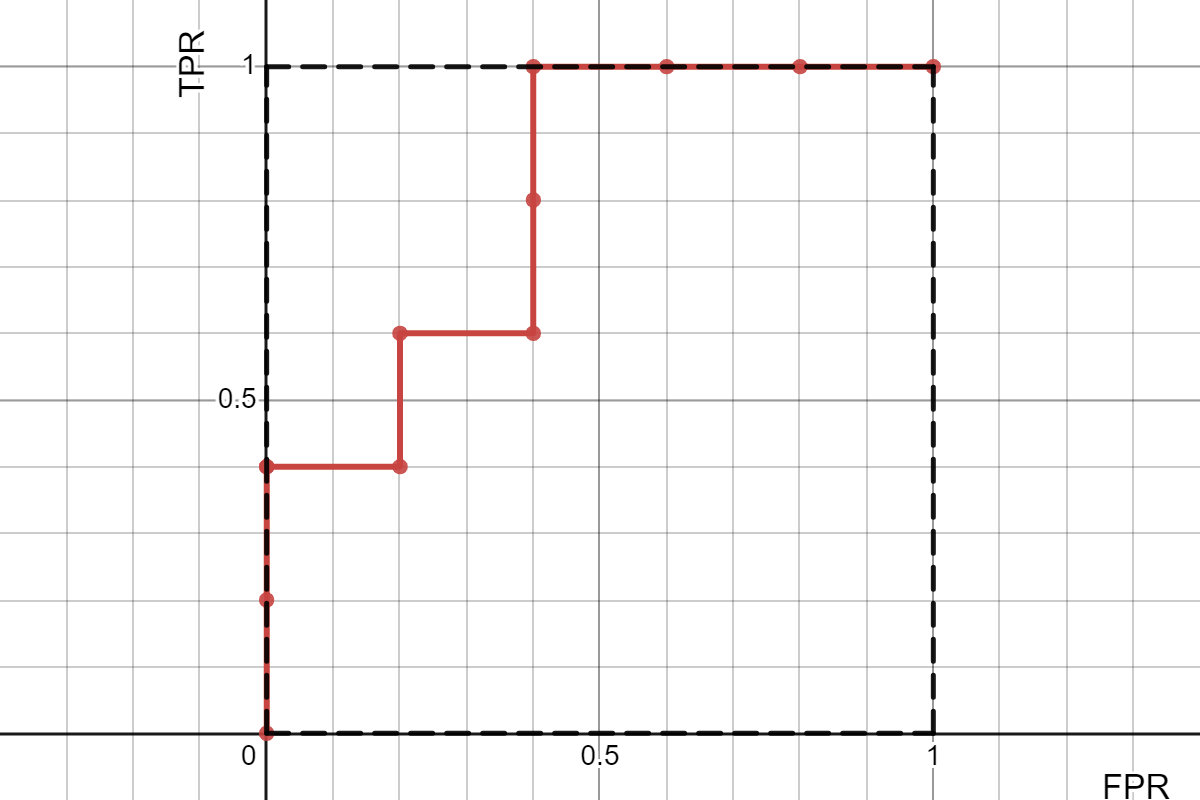
4. AUROC 계산하기
그냥 위 그래프의 넓이 구하면 된다. 구해보면 0.8이다.

sklearn이 검증도 해줬다. sklearn에는 confusion matrix, roc curve 등 여러가지가 구현되어 있으니까 공부하면서 확인해보고 싶으면 유용하게 사용하자!
