로그 함수는 어떤 경우 유용합니까? 사례를 들어 설명해주세요

해당 시리즈에서는 데이터 사이언스 인터뷰 질문 모음집 에서 소개한 질문들에 대한 답변을 다룹니다.

궁금한 사항, 혹은 잘못된 내용 발견시 댓글 부탁드립니다.

---

로그는 근본 자체가 천문학, 항해술 등 큰 수를 쉽게 계산하기 위해 시작되었습니다. 어마어마하게 큰 수들을 작게 변환해서 쉽게 다루기 위해서요.

데이터 분야라고 해서 다른 것은 아닙니다. 큰 수들을 작게 보고싶은 상황에서 많이 사용하죠. 하지만 이 “크다” 라는 것은 언제나 상대적이라는 것에 주목해야 합니다. 100은 큰 수인가요? 비교 대상이 없다면 알 수 없습니다.

따라서 로그함수는 큰 수라는 것이 존재하는 상황, 즉 데이터가 좌측으로 편향 된 상황(left-skewed data)에서, 스케일링을 위해 사용하면 좋습니다.

조금 더 설명하자면, 로그함수는 결국 지수함수의 역함수이기 때문에 수가 exponential하게 변화할 때 사용하면 이를 linear하게 볼 수 있습니다.

좋은 예시

---

예를 들면 시험이 너무 어려워서 990점 만점인 시험인데 100점 미만에 대부분의 학생이 분포되어 있는 상황이 있겠습니다. 이런 시험에서도 900점 이상인 학생들이 있기 마련입니다. 이런 경우 900, 990을 “큰 수” 라고 생각할 수 있고 로그 함수를 이용하면 보다 유의미한 분석이 가능합니다.

아주 간단하게 점수의 분포를 만들어봤습니다.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random

score_low = [random.randint(1, 100) for _ in range(10000)]
score_mid = [random.randint(100, 900) for _ in range(1000)]
score_high = [random.randint(900, 990) for _ in range(100)]
score = score_low + score_mid + score_high

seaborn의 displot을 이용하여 그려봅시다.

sns.displot(score)
plt.plot()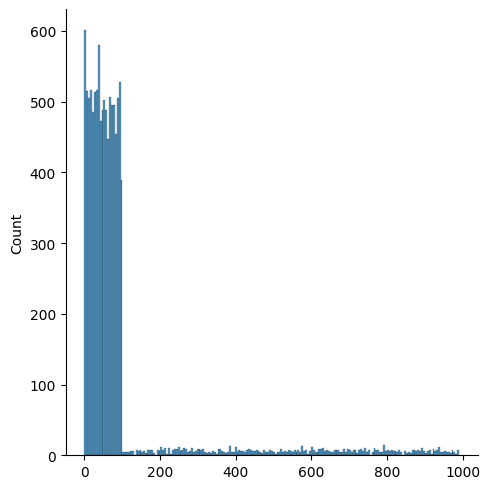

딱 봐도 0~100 사이에 대부분의 점수가 분포하는데, 이 score 변수의 평균을 찍어보면 $98.7$이 나옵니다. 평균이 그다지 의미 있는 숫자가 아닌겁니다. 아주 소수의 상위권이 평균을 끌어올리고 있습니다.

---

이번엔 로그함수를 이용하여 그래프를 그려보겠습니다. 이번 경우에 제가 점수를 임의로 10배 단위로 sampling 했으므로 상용로그를 사용했습니다.

sns.displot(np.log10(score))
plt.plot()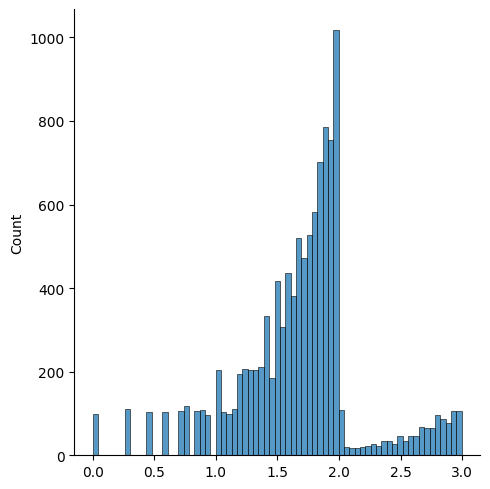

그래프가 아까에 비해서는 조금 더 보기 편해진 것 같습니다. 그래프가 $2.0$에서 끊기는 이유는 샘플링 표본이 $10^2$, 즉 $100$점에서 $10000$개에서 $1000$개로 크게 차이나기 때문입니다.

평균을 구해보면 $1.7$, 로그를 취했으니 다시 $10$의 제곱을 해주면 $47.7$로 조금 더 유의미한 수치를 가져온 것 같습니다.

잘못된 예시

---

위에서 말했듯 로그함수는 큰 수라는 것이 존재하는 상황, 즉 데이터가 좌측으로 편향 된 상황에서, 스케일링을 위해 사용하면 좋습니다.

반대의 경우를 생각해보겠습니다. 위 시험점수 예시에서 score_low와 score_high의 샘플링 수를 바꿔보겠습니다. 즉, 시험이 너무 쉬워서 대부분의 학생이 고득점을 한 상황입니다.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random

score_low = [random.randint(1, 100) for _ in range(100)]
score_mid = [random.randint(100, 900) for _ in range(1000)]
score_high = [random.randint(900, 990) for _ in range(10000)]
score = score_low + score_mid + score_high

해당 시험 점수의 분포는 아래와 같습니다. 순서대로 그냥, 그리고 로그함수를 씌운 결과 입니다.

---

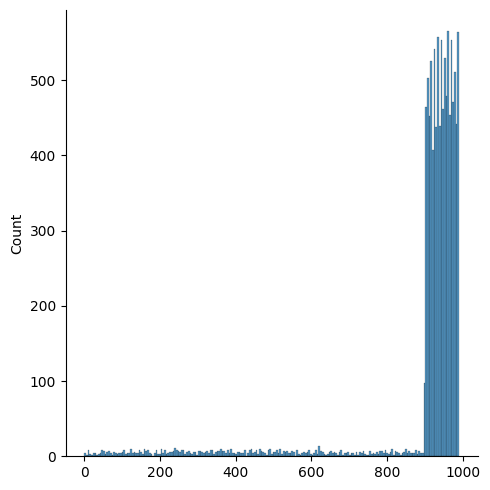
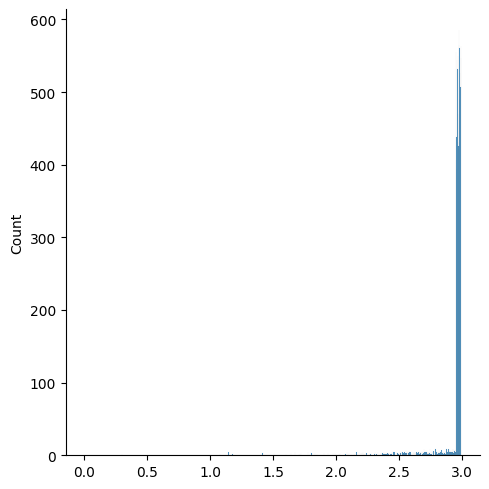
정말 아무짝에 쓸모 없는 그래프가 나왔습니다. 왜냐하면 이 경우는 큰 수가 아닌 작은 수가 존재하는 상황 (right-skewed data)이기 때문입니다. 숫자가 크다고 그냥 무조건 로그함수를 쓰는 것이 아니라, 적절한 상황에 적절한 스케일링이 필요한 것입니다.

그렇다면 이런 right-skewed data인 경우에는 어떻게 할까요? 가장 쉬운 방법은 그냥 데이터 분포를 뒤집어버리면 됩니다. 부호를 바꿔주는게 가장 쉽겠죠? 다만 여기서 주의할 점은 로그함수의 정의역은 양수라는 점입니다. 이를 유의해서 부호를 바꾼 뒤에 적절한 수를 더해주면 될 것 같네요!