중심극한정리는 왜 유용한걸까요?

해당 시리즈에서는 데이터 사이언스 인터뷰 질문 모음집 에서 소개한 질문들에 대한 답변을 다룹니다.

궁금한 사항, 혹은 잘못된 내용 발견시 댓글 부탁드립니다.

---

중심극한정리란?

중심 극한 정리는 모집단에서 추출한 표본들의 평균, 즉 표본평균의 분포가 정규분포를 이룬다는 것을 의미합니다.

이 때 이 정규분포는 평균이 $\mu = m$로 모집단의 평균과 동일하고, 표준편차는 $s = \sigma / \sqrt n$ 으로 모집단의 표준편차를 표본의 크기의 제곱근으로 나눈 값이 됩니다. 다만 여기서 $n$이 충분이 크다는 전제조건이 필요합니다. $n=1$이라면 그냥 모집단과 똑같아지겠죠?

예시와 함께 살펴보기

---

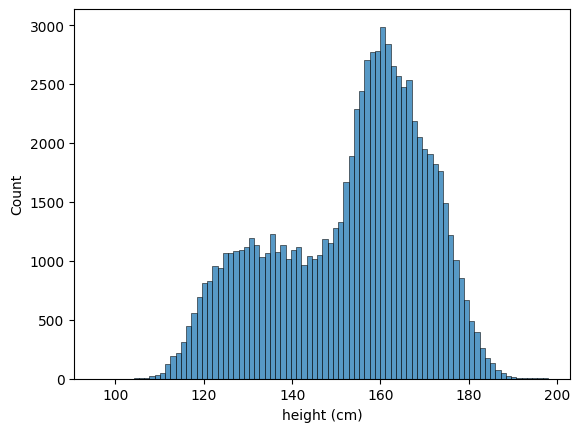
말로만 해서는 잘 모릅니다. 임의로 모집단을 만들어봅시다. 저는 공공데이터포털 에서 학생들의 키를 가져와봤어요. (물론 이 자료도 어떤 모집단의 표본집단이긴 합니다) 총 82,883명의 키 정보가 있었습니다.

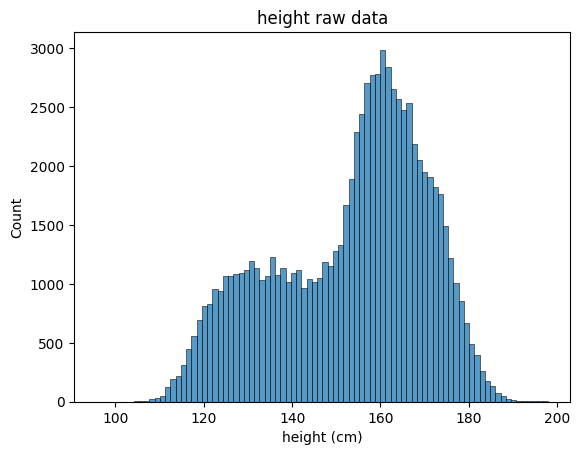
초등학교 1학년부터 고등학교 3학년까지 성별 구분 없이 수집되어 단순한 정규분포와는 거리가 있음을 확인할 수 있습니다. 평균은 $m = 153.1$, 표준 편차는 $\sigma = 17.1$ 입니다.

---

이제 이 데이터에 대해서 중심극한정리가 무엇인지 확인해봅시다. 중심 극한 정리는 표본 평균에 대한 내용이므로 먼저 표본을 뽑아봅시다. 저는 간단하게 $n=10$ 인 표본을 추출해보겠습니다.

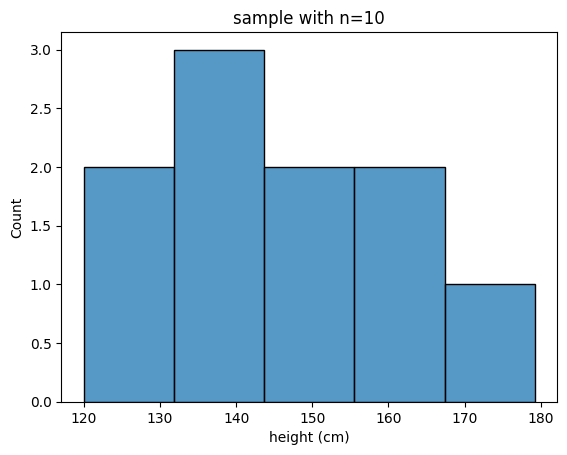
이 표본의 평균은 $146.9$가 나왔네요.

---

이러한 추출을 임의로 100번 반복하고 각 추출마다의 평균을 그래프로 그려봅시다.

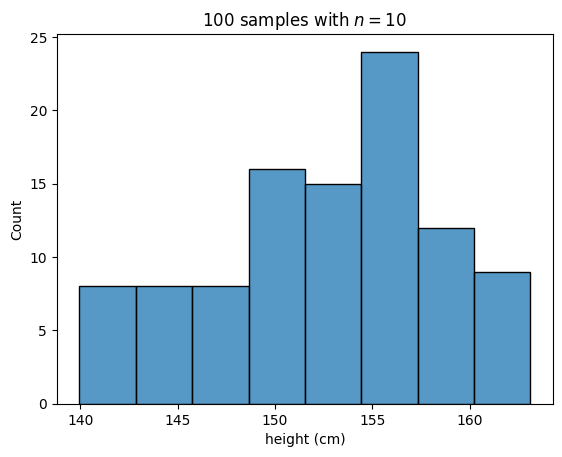
그다지 수치가 충분하지 않아서 제대로 된 그래프가 그려지지 않네요. 10,000번의 추출을 진행해보도록 하겠습니다.

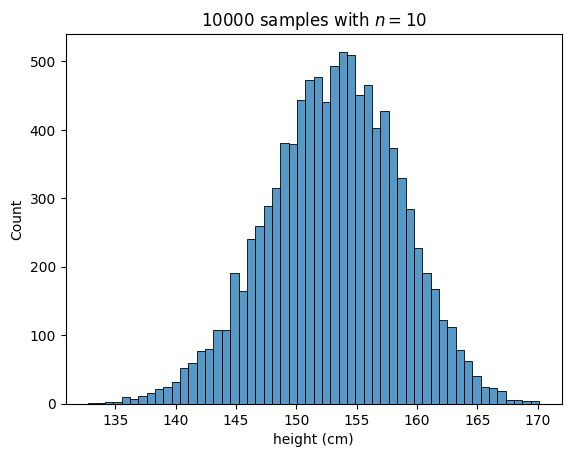
이제 좀 정규분포스러운 그래프가 나타났습니다.

이 분표의 평균과 표준편차는
$\mu = 153.1, \qquad s=5.5$로
$m = 153.1, \quad \sigma/\sqrt n=17.1/\sqrt{10}=5.4$ 와 유사함을 확인할 수 있습니다.

---

추가적으로 $n=1$인 경우를 보면 아래와 같이 sample의 수를 아무리 늘려도 정규분포가 아닌 그저 모집단과 동일한 분포가 나타남을 확인할 수 있습니다.

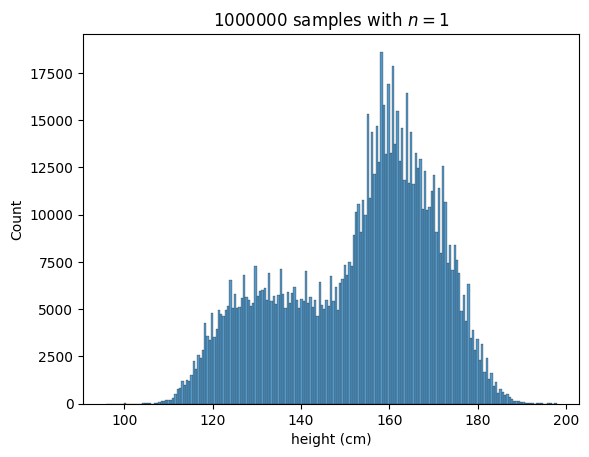
중심극한정리의 장점

---

우리가 사는 실제 세계의 데이터, 즉 모집단은 절대로 다 확인해 볼 수 없습니다. 물론 위 예시는 모집단이 8만개 정도로 다 확인해볼 수 있었지만, 이 또한 사실은 표본이었습니다.

우리는 언제나 표본을 추출해서 이를 통해 모집단을 유추할 수 밖에 없어요. 근데 이 모집단 들은 분포가 참 다양합니다. 언제나 내가 쉽게 분석할 수 있는 normal, 혹은 uniform distribution이길 기도할 수는 없습니다.

여기서 중심극한정리의 강점이 나오는데, 바로 표본평균이 이루는 정규분포는 모집단이 어떻게 생겨있어도 성립한다는 점입니다. 우리는 위 예시에서 모집단을 먼저 확인하고 표본을 추출했는데, 모집단을 확인하지 않았다고 생각해봅시다. 모집단을 모르더라도, 우리는 표본평균을 이용해서 모평균과 모표준편차를 예측할 수 있습니다. ($m=\mu, \quad \sigma=s \sqrt{n}$)

이렇게 예측한 모평균과 모표준편차를 이용한다면 추후 나올 다른 표본평균 또한 쉽게 예측할 수 있게 됩니다.

코드

---

직접 해보고 싶은 분들을 위해 코드를 별첨합니다. jupyter notebook을 이용했습니다.

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

df = pd.read_csv("학생건강검사 키rawdata_2016_20190927..csv", encoding="cp949")

# 전체 데이터 확인
sns.histplot(df["키"])
plt.title("height raw data")
plt.xlabel("height (cm)")
plt.show()
df["키"].mean(), df["키"].std()

# 임의의 10개 데이터 샘플링
sample_10 = df["키"].sample(10, replace=True)
plt.title("sample with n=10")
sns.histplot(sample_10)
plt.xlabel("height (cm)")
plt.show()
sample_10.mean()

# n개의 데이터를 여러번 추출
averages = []
samples = 10000
n = 10
for i in range(samples):
    sample_10 = df["키"].sample(n, replace=True)
    averages.append(sample_10.mean())

sns.histplot(averages)
plt.title(f"{samples} samples with $n={n}$")
plt.xlabel("height (cm)")
plt.show()
np.mean(averages), np.std(averages)