BFS와 DFS

---

• 그래프 탐색 알고리즘
  • 너비 우선 탐색(BFS) : 정점들과 같은 레벨에 있는 노드들을 먼저 탐색하는 알고리즘이다.
  • 깊이 우선 탐색(DFS) : 정점의 자식들을 먼저 탐색하는 알고리즘이다.

예시

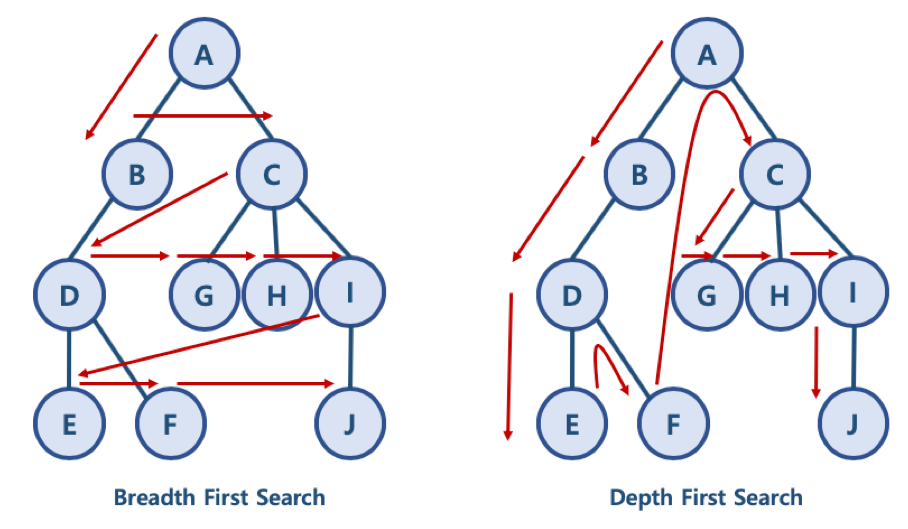
• BFS 방식 : A - B - C - D - G - H - I - E - F - J
  • 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들을 먼저 순회한다.
• DFS 방식 : A - B - D - E - F - C - G - H - I - J
  • 한 노드의 자식을 타고 끝까지 순회한 다음, 다시 돌아와서 다른 형제 노드들의 자식을 타고 내려가며 순회한다.

Python으로 그래프를 표현하는 방법

---

• 파이썬에 제공하는 딕셔너리와 리스트 자료 구조를 활용해서 그래프를 표현할 수 있다.
  
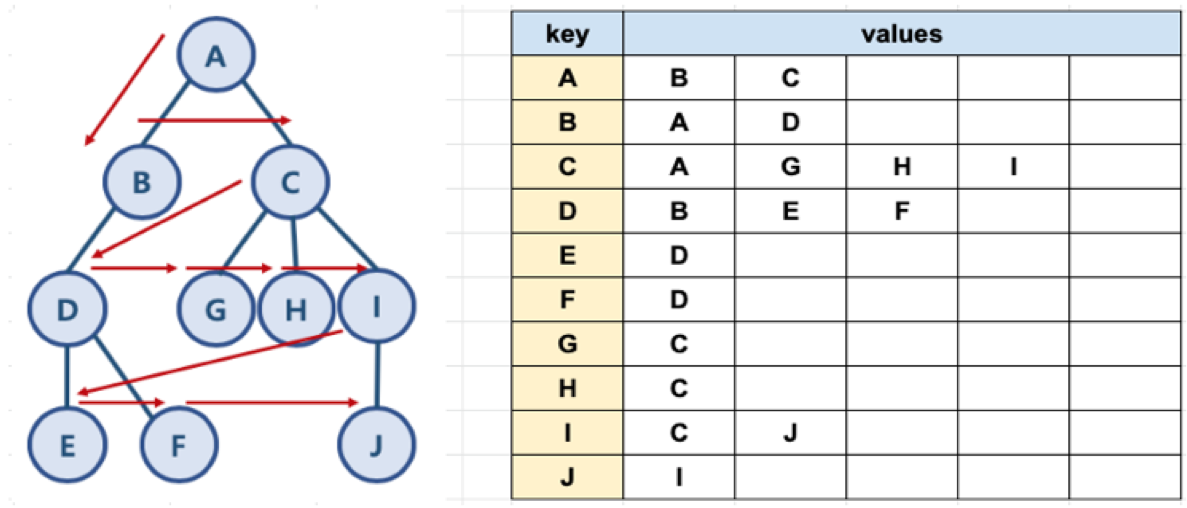
• 각 노드들은 key로, 노드에 연결된 인접노드들은 value로 넣는다.

graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

너비 우선 탐색 구현

시간 복잡도

• 일반적인 BFS 시간 복잡도
  • 노드 수 : V
  • 간선 수 : E
    • 위 코드에서 while need_visit 은 V + E 번 만큼 수행함
  • 시간 복잡도: $O(V + E)$

코드 구현

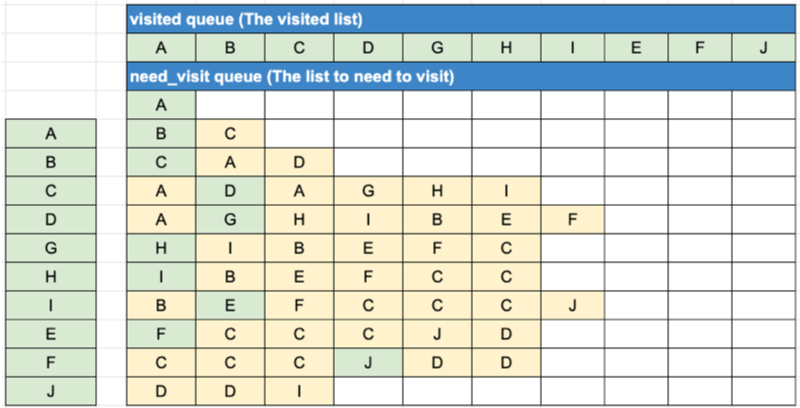
• 큐 2개를 활용하여 방문한 노드를 저장하는 큐(visited)와 방문해야하는 큐(need_visit)를 생성한다.
• 순서
  1. 탐색을 시작할 정점을 need_visit에 저장한다.
  2. need_visit에서 값을 한 개 빼오고, visited에 이미 있는지 확인한다.
     없으면 visited에 저장하고, 정점에 연결된 노드들을(딕셔너리에 저장된 values) need_visit에 저장한다.
     있으면 need_visit에서 다음 값을 빼온다.
  3. 2번을 반복한다.

list 사용

def bfs(graph, start_node):
    # 큐를 사용하는 것이 더 빠르지만, 리스트를 사용하는 것이 편해서 리스트 사용
    visited = list()
    need_visit = list()
    
    need_visit.append(start_node)
    while need_visit:
        node = need_visit.pop(0)
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
    return visited

collections.deque 사용

from collections import deque

def bfs(graph, start_node):
    # Queue보다 deque가 더 빨라서 deque 사용
    visited = deque()
    need_visit = deque()
    
    need_visit.append(start_node)
    while need_visit:
        node = need_visit.pop()
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
    return list(visited)