Casual Representation Learning
혼자 공부하려고 정리하는 글입니다.
Main ref: https://www.lgresearch.ai/blog/view?seq=306
Sub ref: https://lhw0772.medium.com/study-da-domain-adaptation-%EC%95%8C%EC%95%84%EB%B3%B4%EA%B8%B0-%EA%B8%B0%EB%B3%B8%ED%8E%B8-4af4ab63f871
참고: CauSSL: Casuality-inspired Semi-supervised Learning for Medical Image Segmentation
Casual Inference
- 결과에 대한 원인을 찾고 해당 원인이 변경되었을 때 결과에 미치는 영향을 분석 및 추론한느 방법
- 모델의 입력 변화에 따른 출력 변화에 대해 미리 추론함으로써 딥러닝 모델 결과를 예상할 수 있기 때문에 그 특성을 분석할 수 있는 효과가 있음
Independent and identically distributed (i.i.d)
- 데이터를 학습하는 머신러닝에서 중요한 가정은, 새로운 데이터셋에 대하여 학습 성능과 비슷한 성능을 낼 수 있도록 일반화를 보장하는 것
- 대부분의 머신러닝 연구들은 데이터에서 중요한 domain shift, temporal structure 등을 무시하거나 필요 없는 것을 여기고, 대량의 데이터가 갖는 i.i.d의 가정을 이용해 일반화 문제를 해결하려고함
Domain Shift
- 학습데이터와 테스트데이터의 distribution 차이를 의미.
-> 대부분의 머신러닝 알고리즘은 데이터의 분포를 i.i.d로 가정하여 데이터의 수가 많아지면, 학습과 테스트의 분포가 비슷하다고 가정함
-> 하지만, 현실에서는 학습 데이터와 테스트 데이터의 분포가 달라질 수 있음
Learning Reusable Mechanism
- 사람은 기존에 습득한 지식을 바탕으로 새로운 지식을 빠르게 학습함
Casuality Perspective
- 기존의 머신러닝 알고리즘들은 correlation 기반으로 동작하기 때문에 데이터 사이의 상관관계만을 파악할 수 있으며, 인과관계 (Casuality)는 추론할 수 없는 한계가 있음
-> 이 Casuality를 활용한다면 이미 관찬된 상황이나 알고있는 지식과 다른 상황에서도 robust한 예측을 할 수 있음
1. Casual Modeling
-
자연 현상을 모델링할 수 있는 가장 좋은 방법은 Differential equation으로 모델링하는 방법
-
Differential equation을 사용하면 시간에 따른 변화를 모델링할 수 있음
1) 이 변화를 바탕으로 분석해야할 physical system의 state가 앞으로 어떻게 변화할지 예측 가능
2) 원인 및 변수의 intervention 효과에 대해 추론할 수 있음
3) 변수 사이의 통계적 의존성을 파악할 수 있음
4) 인과관계 파악 가능 -
반면, 통계적 모델은 실제 시스템의 표면적인 부분만 모델링할 수 있음. 또한 실험 조건이 변화하지 않는다는 가정 하에 특정 변수가 어떻게 영향을 미치는지 알 수 있음.
-
Casual model은 통계적 모델과 differential equation 모델의 사이에 있음.
-
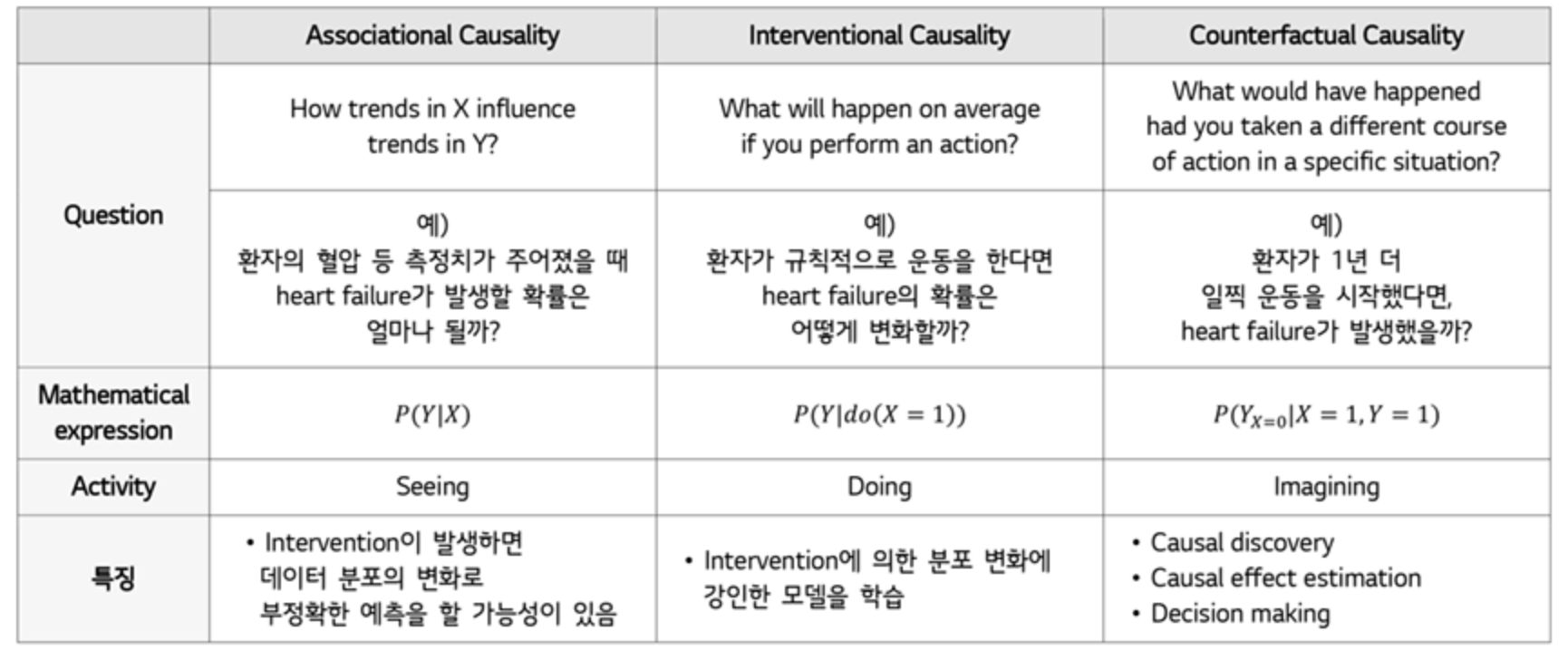
Associational Causality (Predicting in the i.i.d setting)
- 통계적 모델의 목표는 input X와 Target Y가 주어졌을때, 분포 P(Y|X)를 예측하는 것
- 충분히 많은 i.i.d 데이터를 관찰하면 해결 가능
- 하지만, 동일한 실험 조건에서만 정확한 결과를 산출할 수 있으며, 데이터 분포의 변화가 있으면 부정확하게 예측할 가능성이 있음 -
Interventional Casulity (Predicting under distribution shifts)
- 실제 환경에서는 intervention에 의해 데이터 분포에 변화가 발생할 수 있음
- 이 경우 앞서 찾아낸 P(X,Y)가 변하게 되어 기존 통계적 모델의 성능은 보장되지 않음
- 반면, Casual model은 intervention의 효과에 대해 학습하여 데이터 분포 변화에도 강건한 성능을 보임
- Counterfactual Casuality (Answering Counterfactual Questions)
- Casual discovery: 왜 이러한 일이 일어났는지 이유를 알아야함
- Casual effect estimation: 만약 다른 action을 했다면 결과가 어떻게 변할지 알아야함
- Decision making: 원하는 결과를 얻기 위해선 어떠한 action을 취해야하는지 알야아함
2. Independent Casual Mechanisms
Independent Causal Mechanism (ICM) Principle: The causal generative process of a system’s variables is composed of autonomous modules that do not inform or influence each other. In the probabilistic case, this means that the conditional distribution of each variable given its causes (i.e., its mechanism) does not inform or influence the other mechanisms.
- 특정 메커니즘 P(X|PA)을 변화시켜도 다른 메커니즘 P(X,PA)에는 변화가 없음
- 특정 메커니즘 P(X|PA)의 정보를 알아도 다른 메커니즘 P(X|PA)에 대한 정보를 알게되는 것이 아님
*Entanglement: 뒤얽힘, 꼬여있음
- 하나의 z가 다른 특징들과 연관이 되어있어, 특징을 학습할때는 결과에 영향을 미치는 하나의 특징벡터를 구하기가 어려움
3. Sparse Mechanism Shift
Sparse Mechanism Shift (SMS): Small distribution changes tend to manifest themselves in a sparse or local way in the causal/disentangled factorization, i.e., they should usually not affect all factors simultaneously.
- SMS는 ICM의 결과로, causal/disentangled factorization에서 intervention을 통해 분포를 변화시켰을 때 소수 또는 특정 부분의 component만 변화하는 경향을 의미
- 이는 만약 intervention의 결과로 모든 componet가 변한다면 모델은 intervention을 통한 분포의 변화로부터 어떠한 정보도 배우기 어렵다는 것을 의미
Casual leraning의 목적은, 현실 세계를 독립적인 casual mechanism의 chain으로 간주하며, 결국 현실 세계를 casual structure를 가진 disentangled representation으로 모델링하는 것
4. Implications for Machine Learning
- Learning Transferable Mechanisms: 현실 세계에서 데이터의 양은 제한되기 때문에 데이터 분포에 온전히 의존하기 어려움. 또한 하나의 component로 규명하기 어렵기때문에 현실 세계를 모듈형태로 구조화하는 것이 중요
Semi-Supervised Learning
- 데이터 라벨이 부족한 현실에서의 문제를 해결하기 위해 제안
- SSL이 어떻게 동작하는지 정확하게 밝혀지지 않아 해석적 연구가 필요
ex) X->Y의 casual 관계라 할때, 모델은 X->Y로 mapping을 학습
- ICM에 의하면 P(x)와 P(Y|X)는 서로 독립, 어떠한 정보도 공유하지 않음: P(X)를 P(Y|X)의 추정에 활용하고자 한다면 아무런 도움이 되지 않음
- 반면에 anti-casual 관계 (Y->X)를 학습하여 ssl이 가능하다는 것을 증명
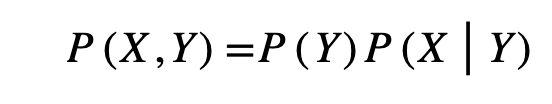
Robustness and Strong Generalization
- Robustness와 Generalization은 OOD문제로 생각
- OOD문제는 distribution class로부터 empirical risk를 최소화하는 최적화 문제로 간주 가능
- OOD의 gap은 학습 분포 P(X,Y)와 테스트 분포 P*(X,Y)의 차이에 의해 발생
- Casuality 관점에서 보면, OOD의 P*(X,Y)를 특정 intervention의 결과로 간주할 수 있음
Future work of Casual Representation Learning
- 비선형 인과관계 학습
- Learning casual variables
- Understanding the biases of existing dl: 추출된 disentangled representation에서 어떤 component가 새로운 task에 도움이 되는 지 이해
