[OpenCV] 미분의 의미와 Laplacian 필터 구현

1. 미분의 의미

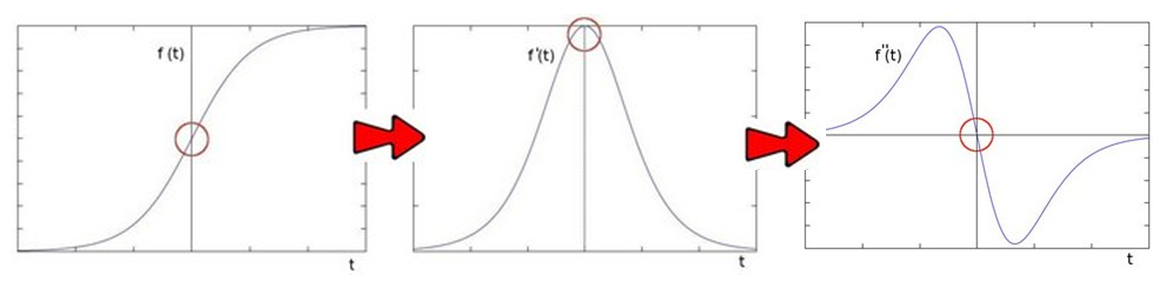
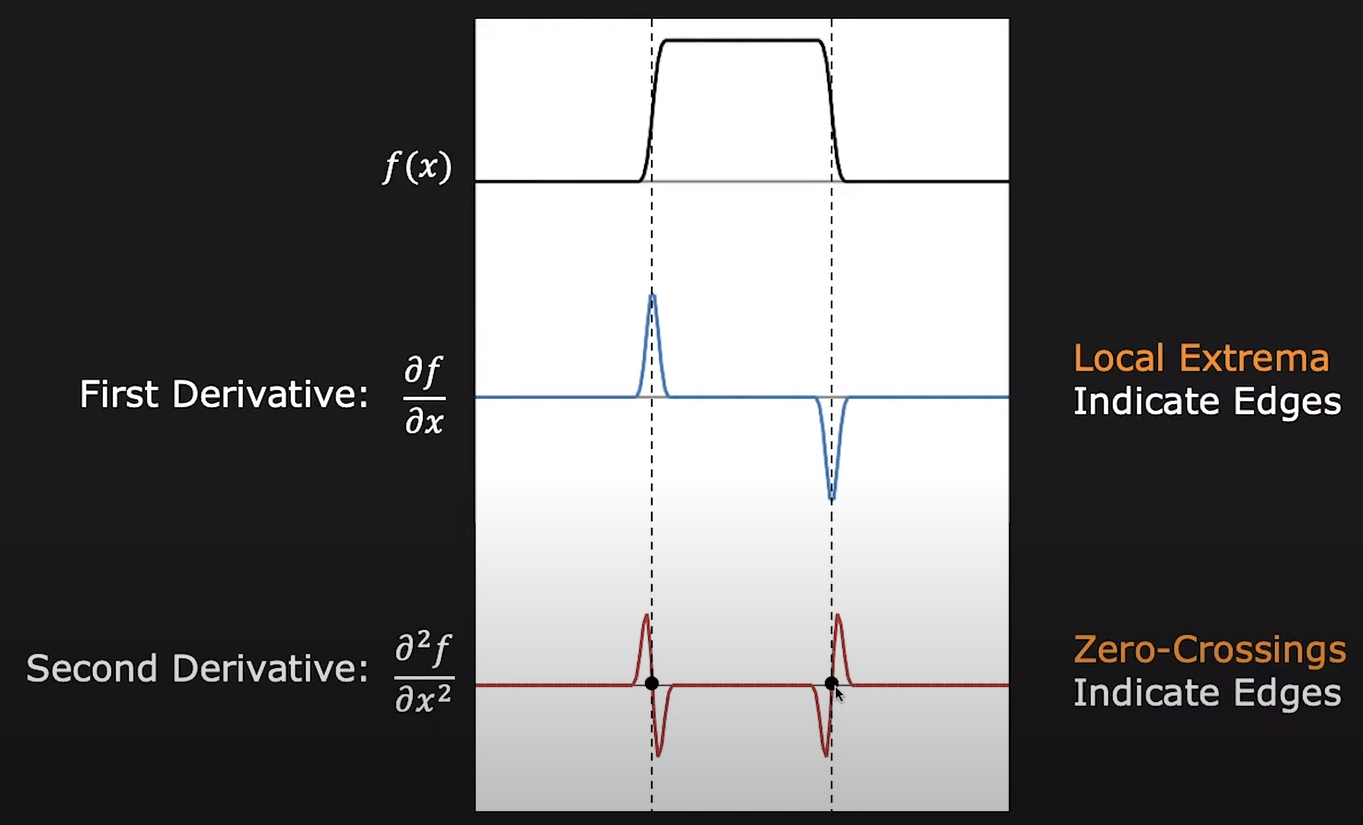
 에지는 이미지에서 픽셀값이 급격히 변화하는 지점이다. 미분은 이 변화를 표현하는 훌륭한 수단이다. 위 첫번째 그림에서 픽셀값은 작은 값에서 큰 값으로 급격히 변화하고 있기 때문에 빨간 동그라미 부분은 에지일 것이다.

 이때 함수를 미분하면 에지를 좀 더 명확히 찾을 수 있다. 두번째 그림과 같이 에지에서는 미분값이 최대(혹은 최소)가 된다. 하지만 이미지에서는 여러 local maxima가 존재하기 때문에 에지를 검출하기 위해 적절한 threshold를 직접 설정해주어야 한다. 또한 threshold를 이용하기 때문에 에지의 위치가 여러 개의 픽셀로 표현될 수 있다.

 함수를 한 번 더 미분하면 세번째 그림과 같이 에지에서 미분값이 zero-crossing된다. zero-crossing되는 지점만을 찾으면 되기 때문에 threshold를 설정하지 않아도 되고, 에지의 위치가 한 픽셀로 표현되는 장점이 있다.

2. 노이즈 제거

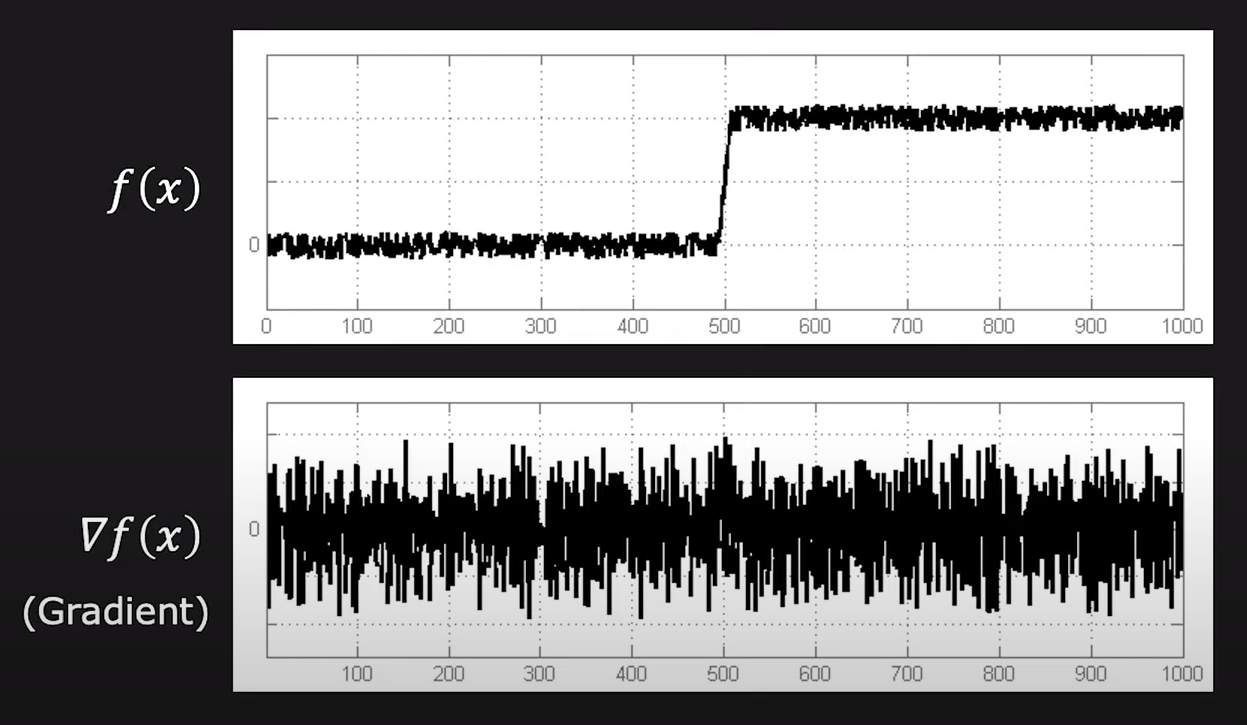
 위 첫번째 그림에서는 픽셀값이 급격히 변화하는 에지가 500 부근에서 하나 존재할 것이다. 하지만 이미지에 노이즈가 존재하기 때문에 이를 제거하지 않고 미분할 경우, 두번째 그림과 같이 수많은 local maxima(또는 minima)가 존재하게 된다. 그렇기 때문에 Gaussian Blur 등을 활용해 노이즈를 제거해줄 필요가 있다.

3. Laplacian 수식

4. 구현

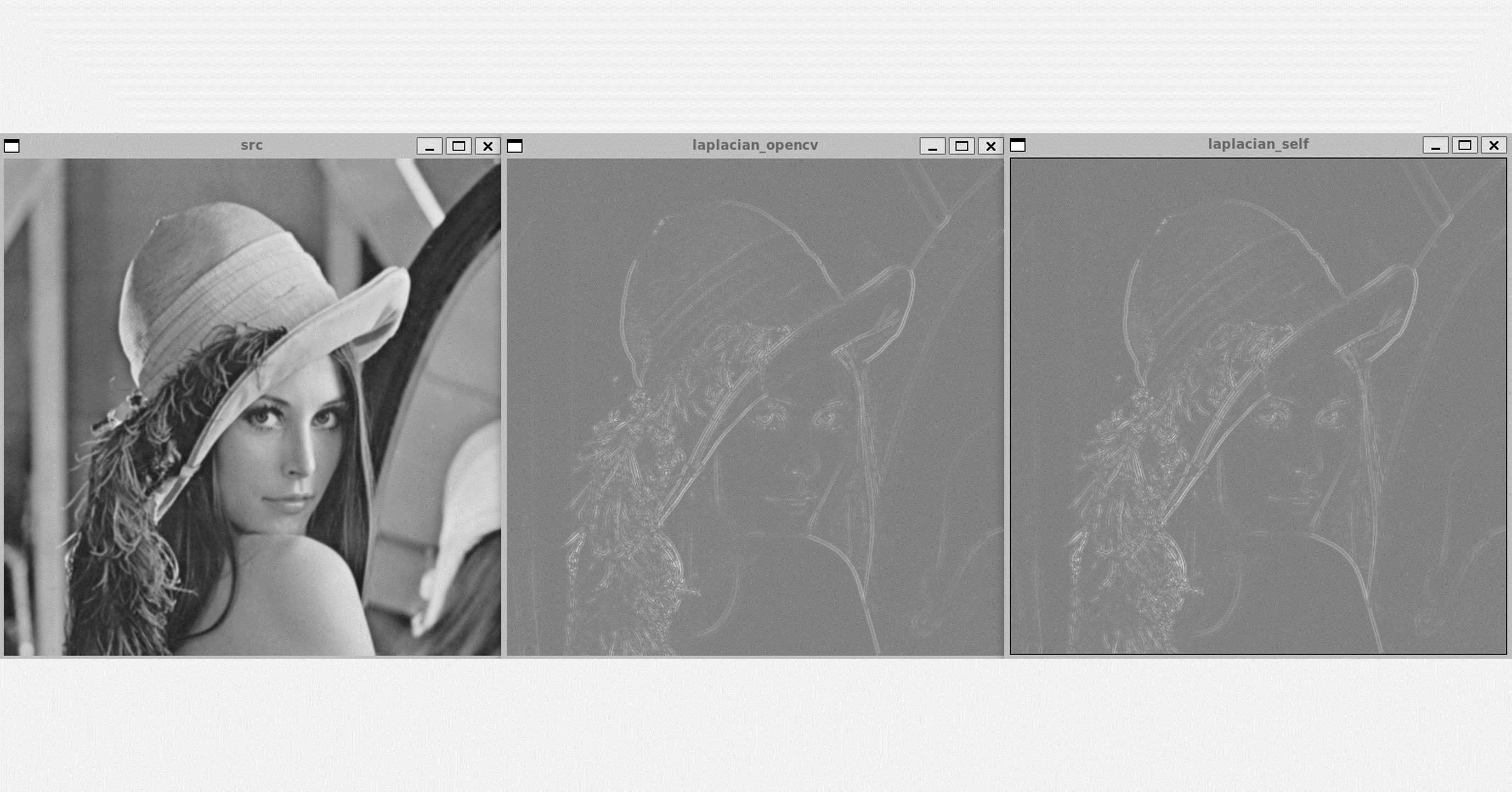
4.1. 결과

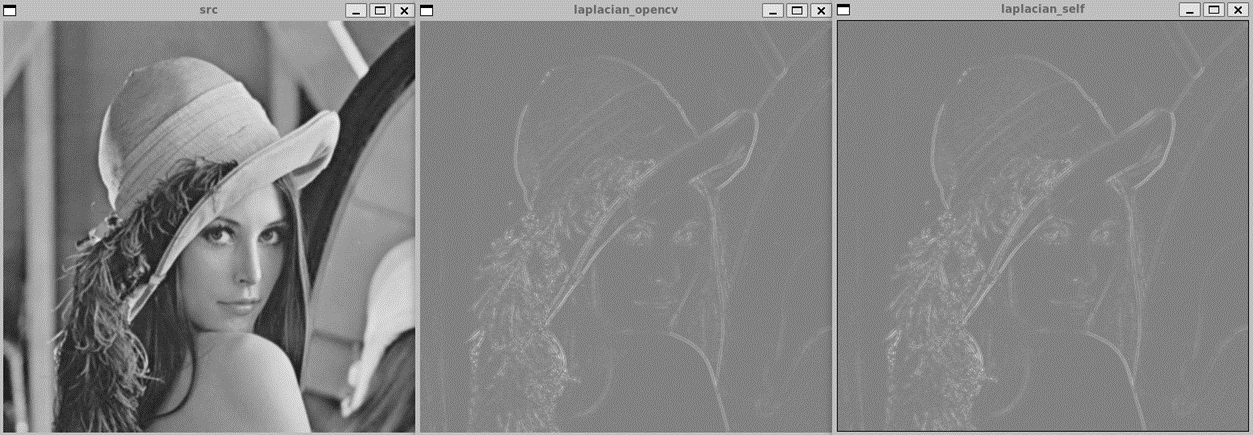
더 나은 시각화를 위해 laplacian 적용 후 모든 픽셀에 128을 더해주었다.

4.2. 코드

#include <opencv2/opencv.hpp>

int main()
{
    cv::Mat src = cv::imread("/home/jiwon/workspace/test/lenna.bmp", cv::IMREAD_GRAYSCALE);
    cv::GaussianBlur(src, src, cv::Size(3, 3), 0);

    cv::Mat laplacian_opencv;
    cv::Laplacian(src, laplacian_opencv, CV_16S);
    cv::convertScaleAbs(laplacian_opencv, laplacian_opencv);
    laplacian_opencv = laplacian_opencv + 128;

    cv::Mat laplacian_self(src.size(), CV_8UC1);
    for (int y = 1; y < laplacian_self.rows - 1; ++y)
    {
        for (int x = 1; x < laplacian_self.cols - 1; ++x)
        {
            int center = src.at<uchar>(y, x);
            int top = src.at<uchar>(y - 1, x);
            int bottom = src.at<uchar>(y + 1, x);
            int left = src.at<uchar>(y, x - 1);
            int right = src.at<uchar>(y, x + 1);

            laplacian_self.at<uchar>(y, x) = cv::saturate_cast<uchar>(abs(top + bottom + left + right - 4*center) + 128);
        }
    }

    imshow("src", src);
    imshow("laplacian_opencv", laplacian_opencv);
    imshow("laplacian_self", laplacian_self);
    cv::waitKey(0);

    return 0;
}

---

📙 참고

• OpenCV - Laplacian Operator