[OpenCV] 히스토그램 스트레칭과 평활화

1. 히스토그램 스트레칭

• 영상의 히스토그램이 그레이스케일 전체 구간에 걸쳐 나타나도록 변경하는 선형 변환 기법
• 최솟값과 최댓값 부근에 픽셀의 개수가 적을 경우, 더 효과적인 명암비 향상을 위해 양쪽 일정 퍼센트의 픽셀을 제외하고 스트레칭을 수행할 수도 있다.

1.1. 변환 함수

• 그래프
  

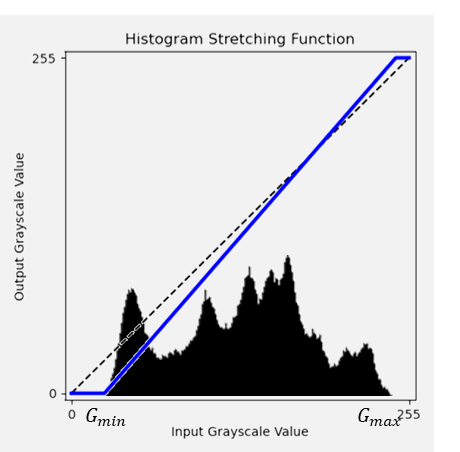
• 수식

  $y = ax + b \\ \,\\ a = {255 - 0 \over G_{max} - G_{min}} \\ \,\\ y = {255 \over G_{max} - G_{min}}(x - G_{min}) \\ \,\\ \therefore \, dst(x, y) = {src(x, y) - G_{min} \over G_{max} - G_{min}} \times 255$

1.2. 구현

minMaxLoc()으로 직접 구현하거나 normalize()를 이용한다. (참고)

#if 0
    double gmin, gmax;
    minMaxLoc(src, &gmin, &gmax);

    Mat dst = (src - gmin) / (gmax - gmin) * 255;
#else
    Mat dst;
    normalize(src, dst, 0, 255, NORM_MINMAX);
#endif

1.3. 적용 결과

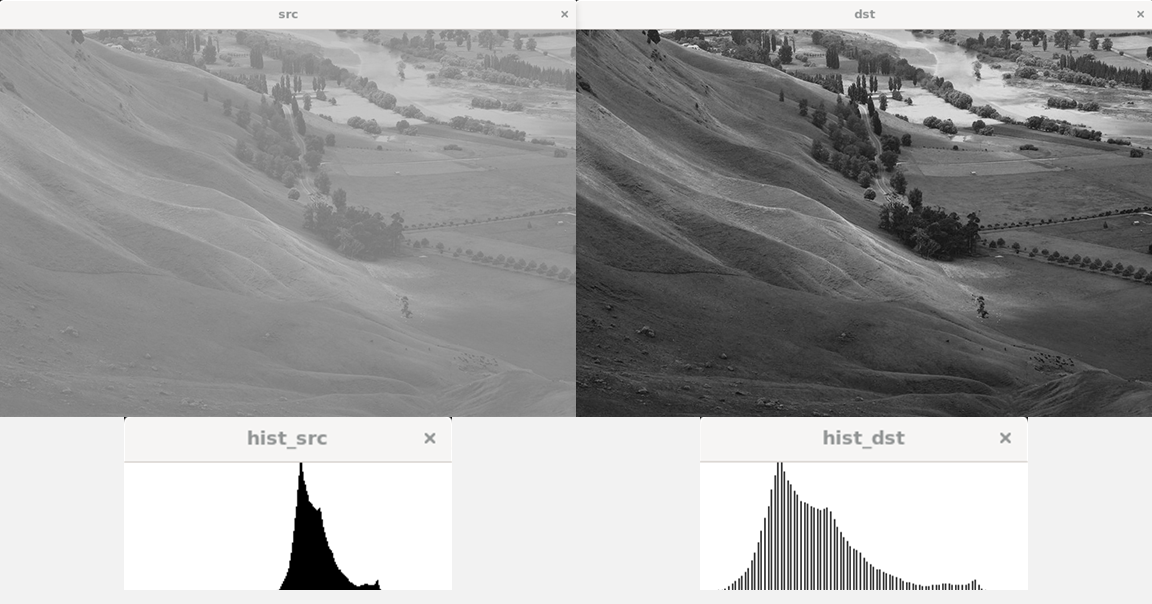
• 명암이 모호하던 좌측 원본 사진에 비해, 히스토그램 스트레칭을 적용한 우측 사진은 명암이 뚜렷해졌다.

2. 히스토그램 평활화(Equalization)

• 히스토그램이 그레이스케일 전체 구간에서 균일한 분포로 나타나도록 변경하는 명암비 향상 기법

2.1. 변환 함수

• 그래프
  

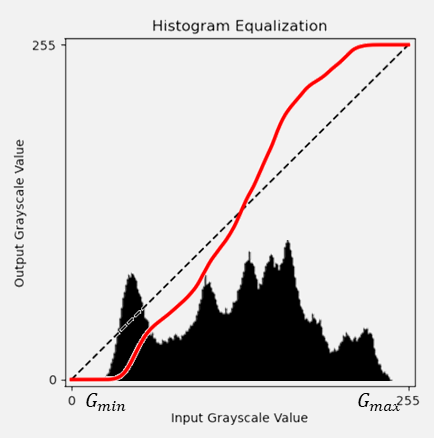
• 수식

  • 히스토그램 함수 구하기: $h(g) = N_g$
  • 정규화된 히스토그램 함수 구하기: ${p(g) = h(g) \over w \times h}$
  • 누적분포함수(cdf) 구하기: $cdf(g) = \sum_{0 \le i \le g} p(i)$
  • 변환 함수: $dst(x, y) = round(cdf(src(x, y)) \times L_{max}$

2.2. 구현

이중 for문으로 직접 구현하거나 equalizeHist()를 이용한다.

void equalizeHist(InputArray src, OutputArray dst);

2.3. 적용 결과

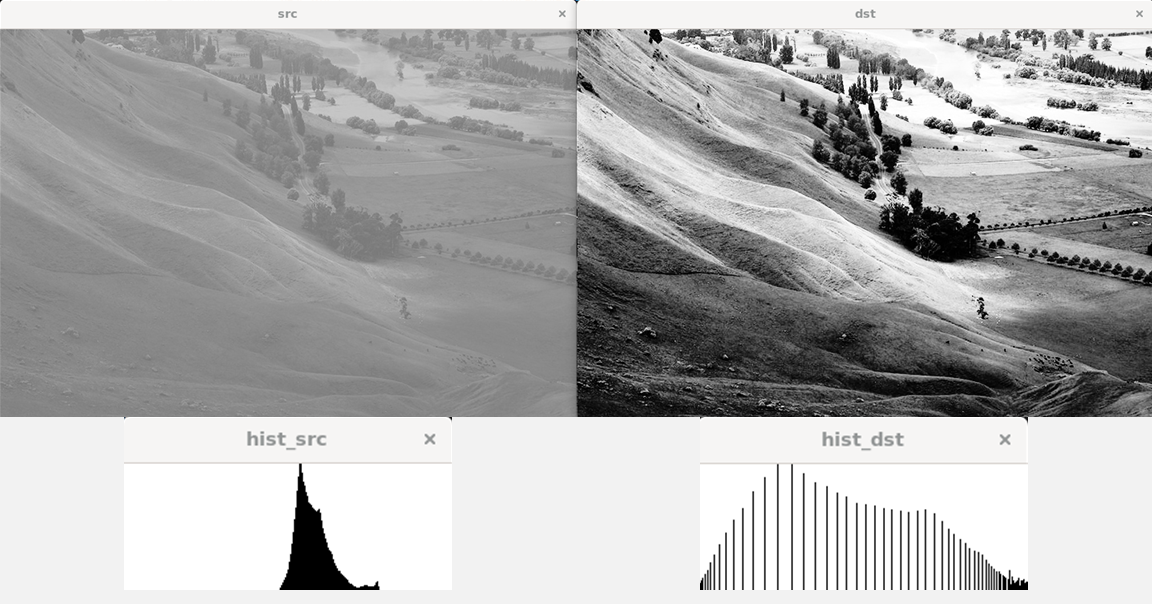
• 명암이 모호하던 좌측 원본 사진에 비해, 히스토그램 스트레칭을 적용한 우측 사진은 명암이 뚜렷해졌다.
• 평활화한 히스토그램의 구역을 균등하게 나누면 각 구역의 픽셀 개수는 동일하다.

3. 히스토그램 스트레칭 vs. 평활화

• 사람의 눈으로 보았을 때, 어느 한쪽이 항상 좋다고 말할 수는 없다. 사람마다, 영상마다 달라질 수 있다.

---

📙 강의 - 강사 황선규