경희대학교 황효석 교수님의 2021-2 로봇 프로그래밍 수업을 듣고 공부한 것입니다.
Bayes Filter

현재의 나의 state 를 알기 위해서는
- 바로 전 단계의 state
- 직전에서 현재 state 로 넘어가기 위한 명령 u
- 현재의 state 에서 주변 환경으로부터 획득한 정보 z
이 세 가지의 값이 있으면 우리는 매 단계마다 state 를 업데이트 할 수 있다.
베이즈 필터는 두 단계로 나눌 수 있다.
Prediction
과거의 state 와 command 를 이용해서 현재의 state 를 예측하는 단계.
Correction
measurement 를 통해 잘 예측했는지 , 잘 예측하지 못 했다면 어떻게 수정해야 하는지 판단하는 단계.
Kalman Filter
칼만 필터는 Bayes Filter 의 일종이다.
- Estimator for the linear Gaussian Case.
확률을 계산하는 state 와 state 간의 관계가 선형적일 때 칼만 필터를 사용한다.
- Optimal solution for linear models and Gaussian Distributions
linear 라는 조건을 만족하면 확률분포를 Gaussian distribution 으로 나타낼 수 있다.
Gaussian Distribution 의 장점 : non-parametric distribution 과는 달리 몇 개의 값만 있으면 모든 variable 에 대한 확률 분포를 알 수 있다. 가우시안의 경우에는 평균과 분산.
하지만 이 가우시안 확률 분포를 계속 유지하기 위해서는 식이 linear 해야 한다는 제약 조건이 있다.
칼만 필터는 베이즈 필터의 일종인데, 계산되는 모든 식이 linear equation 이고 모든 확률 state 나 노이즈의 확률 분포들은 모두 가우시안 분포를 따른다고 가정한다.
Filter
필터는 기능이 있는 알고리즘이다. 무언가 입력이 있을 때 어떤 것은 통과시키고 나머지는 버리거나 상쇄된다.
칼만 필터의 경우, 노이즈나 부정확한 값은 제거되고 그나마 정확해보이는 값이 통과된다.
칼만 필터는 정보를 합했을 때 얻어지는 추정 오차를 최소화 하도록 구성된다. 추정 오차를 최소화하는 칼만 상수를 구하면, 결론적으로 추정 오차와 표준 편차가 점점 줄어들게 되어 원하는 참값에 근접한 추정치를 구할 수 있게 된다.
우리는 예상값과 측정값 둘 중에 어떤 것을 믿을 것인가?
Case #1
비가 올 것이라는 기상 예보가 있었는데 하늘은 맑다. 우산을 가져 갈 것인가 말 것인가?
-> 믿을 만 한 방송국이라면 우산을 들고 나가고, 맨날 틀리는 방송국이라면 우산을 안 들고 간다.
Case #2
키는 정확하게 측정하지만 몸무게는 부정확한 센서 하나,
키는 부정확하게 측정하지만 몸무게는 정확한 센서가 있다. 어떻게 정확하게 키와 몸무게를 측정할 것인가?
-> 첫 번째 센서로는 키를, 두 번째 센서로는 몸무게를 측정한다.
예상값과 측정값이 있을 때 우리는 어떤 값을 더 신뢰해야 하나? -> 더 믿을 만한 것을 믿는 것이 좋다.
Linear Gaussian Distribution
we only have to consider mean and variance of states.
우리는 확률분포를 Gaussian Distribution 으로 가정하기 때문에 mean 과 variance 값만 가지고 계산할 수 있다.
Kalman Filter in 1D
자율주행을 하기 위해서는 state 와 랜드마크들이 2차원 이상의 값을 가져야 한다. 하지만 처음에는 빠른 이해를 위해 1차원을 먼저 다루어 보자.
Prediction: summation of Gaussian Distribution.
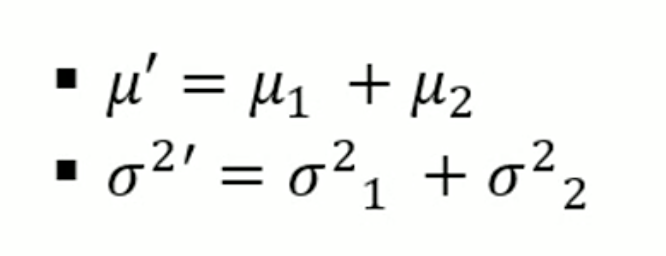
이전 state 에 대해서 현재 state 로 값을 추정하는 것.
Gaussian Distribution 의 합으로 Prediction 을 추정한다.
두 개의 분포를 더한다고 했을 때, 새로운 분포의 평균은 이전 평균들을 합한 것이고 분산도 이전 분산들을 합한 것이다.
따라서 prediction 은 매우 구하기가 쉽다. 예를 들어 이전 state 의 모션을 줬다고 하면, 이전 state 에 모션을 준 새로운 state 의 평균은 두 개의 확률 분포를 더하고 분산도 더하면 된다는 것이다.
예를 들어, 10 이라는 위치에서 5만큼 더 모션을 줬다고 하면 이후 위치는 15가 된다.
두 개의 가우시안 분포를 더하면 결과값도 가우시안 분포가 된다.
Update: production of Gaussian Distribution
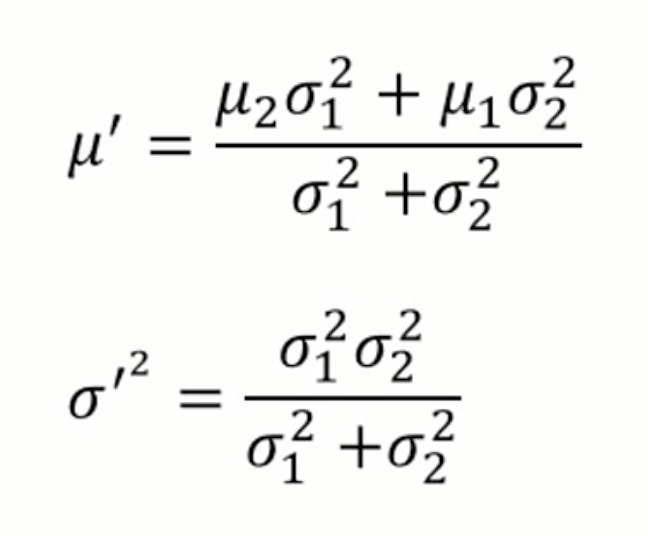
어떤 두 개의 분포가 있을 때 최종적인 결정은 두 개의 분포를 곱해서 나온 값을 채택하겠다는 것이다.
예를 들어, 첫 번째 센서는 키가 160이 나왔는데 분산이 매우 크다고 해 보자.
두 번째 센서는 170이 나왔는데 분산이 매우 적다.
그렇다면 실제 값은 170에 더 가깝다고 볼 수 있다.
내가 추정을 해서 나온 확률값과 내가 측정해서 나온 확률값을 곱하면 최종적인 확률분포 (Posterior Belief) 를 얻을 수 있다.
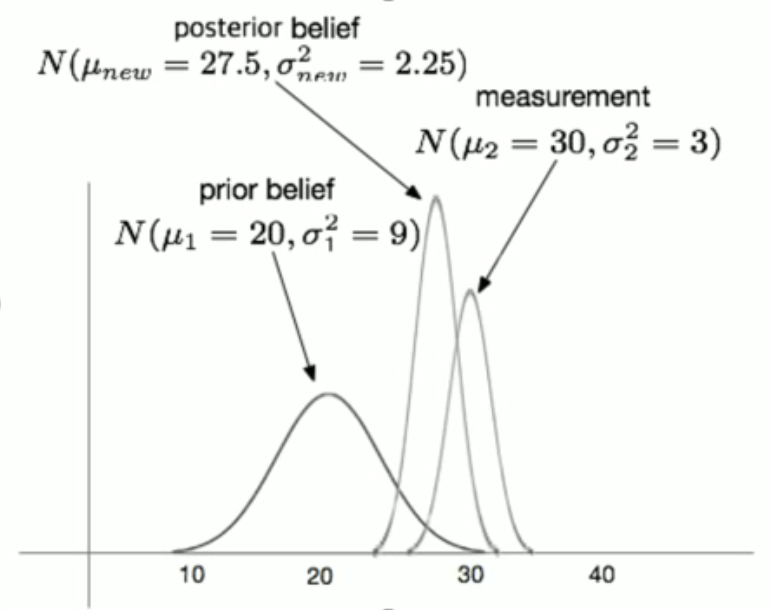
위 사진의 경우, measurement 의 belief 가 prior 의 belief 보다 작기 때문에 measurement 쪽에 더 가까이 최종적인 확률 분포가 정해진다.
따라서 u' 식을 보면, u1 의 variance 가 클 수록 u2 의 가중치가 커진다.
과연 결과값도 가우시안 분포를 따를까?


그래서 칼만 필터는 무엇인가?
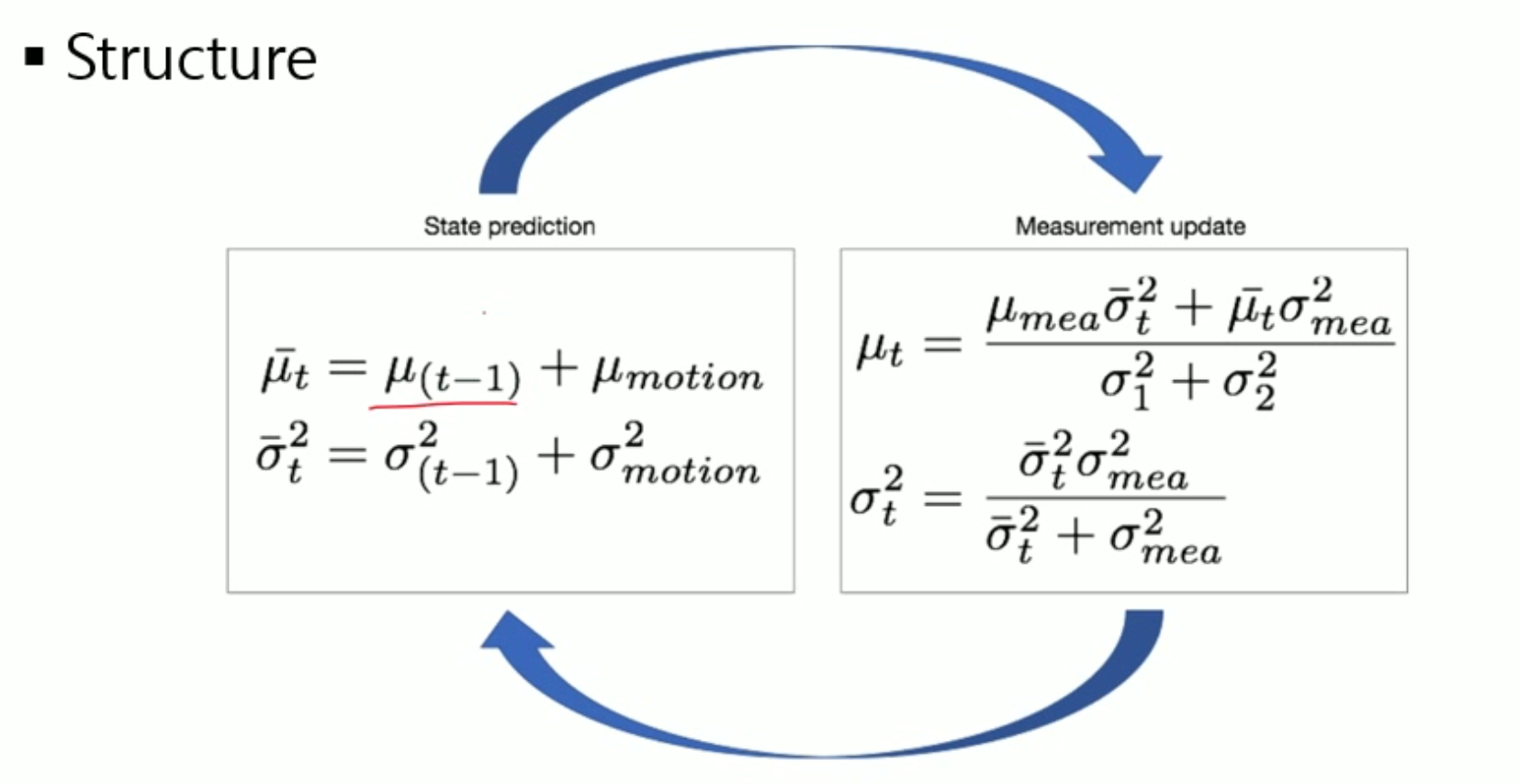
- 매 스텝마다 이전 state 에서 모션을 주면
평균도 + 로 업데이트하고, 분산도 + 로 업데이트한다.
이것은 최종이 아니라 Prediction 한 값이기 때문에, 위에 bar (혹은 hat)를 붙인다.
중요한 것은 최종적인 값이 아니라 최종적인 값을 구하기 위한 중간 단계의 값이라는 것이다.
-
1에서 구한 Prediction 과 measurement 값을 곱해서 최종적인 값을 정한다.
-
이 최종적인 값이 그 다음 스텝의 input 으로 들어가는 것이다.
칼만 필터는 Recursive 하게 동작한다.
Kalman Gain
칼만 게인은 그냥 식을 간단하게 만들고 보기 쉽게 하기 위해서 설정한 상수이다.
두 식에 공통적인 부분을 찾을 수 있으므로 그것을 빼내서 따로 정의하는 것이다.
칼만 게인은 분포가 어떤 식으로 되어 있는지를 반영한다.
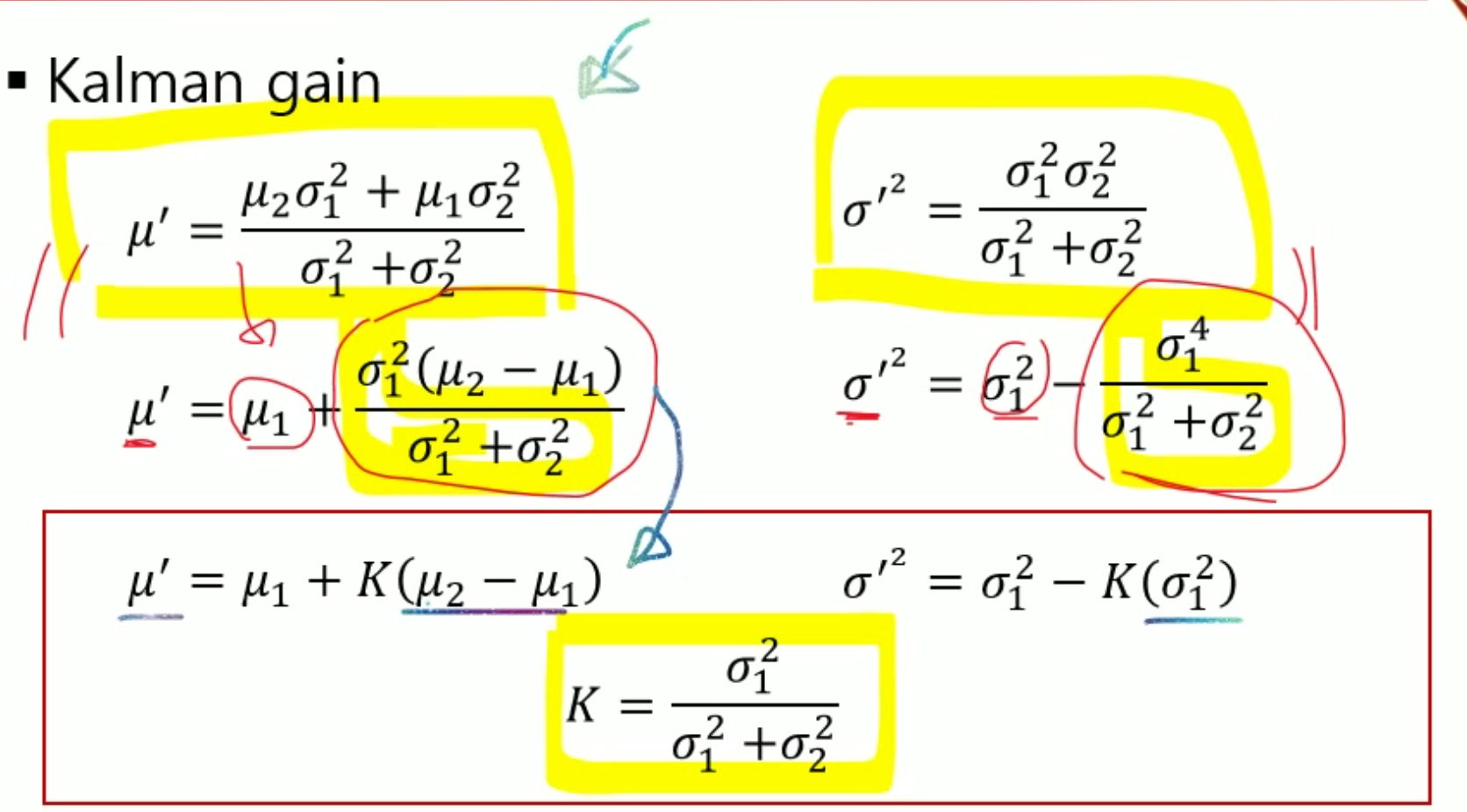
- 만약 sigma 2 가 정말 클 때
K 는 0 에 가까워질 것이며, u2-u1 값을 사용하지 않게 된다. 그러면 업데이트할 때 u' 은 u1 을 더 많이 반영하게 될 것이다.
- 만약 sigma 1 이 정말 클 때
K 는 1 에 가까운 값을 갖게 된다. 그렇다면 u1 - u2 + u1 = u2 가 되며 u' 은 u2 를 더 많이 반영하게 될 것이다.
즉, Prediction 의 분산이 작으면 Prediction 값을 많이 쓰고, Measurement 의 분산이 작으면 Measurement 값을 많이 사용하겠다는 것이다.
Multivariate Case
다중 변수를 다룰 때 칼만 필터의 작동 원리
State Prediction

x 는 state 고, u 는 control 이다. P 는 Covariance Matrix 이다.
Variance 는 스칼라에 대해서 분산을 나타낸 것이고, 랜덤 변수가 벡터 형태를 가지게 된다면 그 variance 는 covariance 를 가지게 되는 것이다.
-
이전 state 에, 어떤 control 값 (Transition Matrix) 를 곱해서 더한 것이 내가 현재 추정하는 새로운 state 이다.
-
x(k-1) 이 F 를 곱해서 새로운 x(k) 가 되었을 때, P 는 이전 covariance matrix 에 F 를 곱한다고 P 가 되는 것이 아니라 앞뒤로 곱해줘야 한다.
-
Q 는 노이즈를 의미한다. 명령을 내렸는데, 그것이 100% 전달이 되지 않을 수도 있다. 따라서 command 와 실제 로봇이 움직인 것의 차이를 노이즈로 표현하고, 이들을 Q 로써 결과값에 반영해준다.
x 는 위에서 봤던 확률변수의 mean 개념을, P 는 variance 의 개념을 담고 있다.
Update
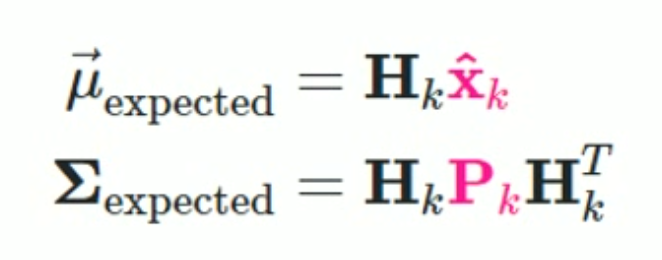
Prediction 한 결과값을 가지고 Expected 를 구한다.
Expected : 내가 계산한 것을 가지고 H 를 구했을 때, 어떻게 보이나?
예를 들어 x 가 map 이라면, measurement 는 map 이 아니라 랜드마크들의 위치가 될 것이다.
그때 H 의 역할은 맵에서 현재 위치에 따라서 랜드마크들이 어떻게 보일 것인가? 하는 것을 변환하는 행렬일 수 있다.
즉, H 는 prediction 을 한 distribution 을 가지고 measurement 와 비교하기 위해 measurement level 로 transition 해주는 행렬이다.



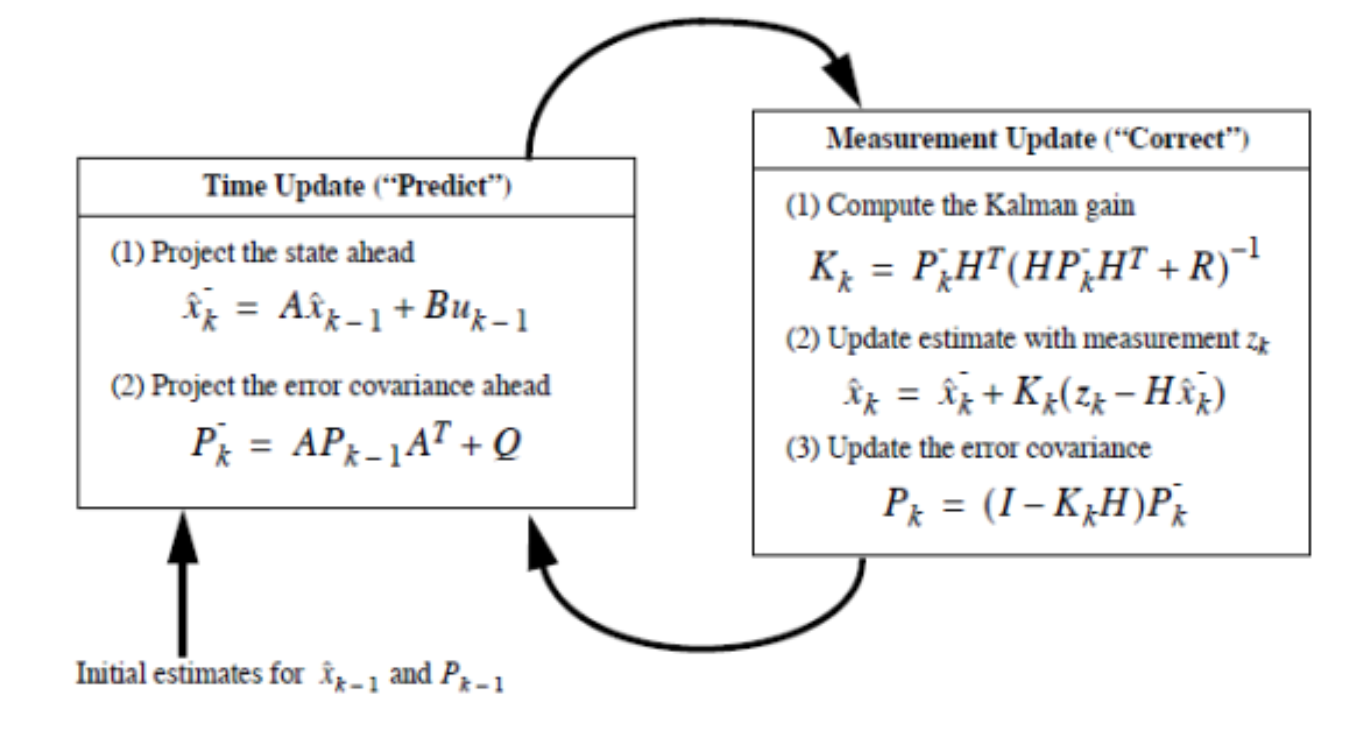
-
기존의 state 와 control 이 있을 때 걔네들에 각각 Transition Matrix 를 곱하고 Q 를 더해서 평균과 Covariance 를 다시 정해준다. (Prediction)
-
이들을 이용해서 Kalman Gain 을 구해준다.
-
Kalman Gain 을 이용해 Predicted Measurement 와 Observed Measurement 를 곱한다.
-
그 곱한 Distribution 의 평균과 Covariance 를 새롭게 구한다.
-
이들을 다시 next step 에 넣어준다.
실제 코드
def kalman(x, P, measurement, R, motion, Q, F, H):
# UPDATE x, P based on measurement m
# distance between measured and current position-belief y = np.matrix(measurement).T - H * x
S = H * P * H.T + R # residual convariance
K = P * H.T * S.I # Kalman gain
x = x + K*y
I = np.matrix(np.eye(F.shape[0])) # identity matrix
P = (I - K*H)*P
# PREDICT x, P based on motion x = F*x + motion
P = F*P*F.T + Q
return x, P문제점
과연 모든 문제들이 Linear 하게 표현될 수 있나? 곱하기와 더하기만으로 표현 가능한가?
