1. Introduction

• In-context Learning $\rightarrow$ important emergent capability of LLM

  • without updating the model parameter, LLM can solve various problem
  • this ability is extracted from training corpus and emerge at scale

• After GPT3, ICL has been the subject of a growing body of research

  • lots of research focused on In-Context Supervised Learning (ICSL)

• Many application demand the use of ML model for decision making

  • In-Context Reinforcement Learning (ICRL) + sequential decision making is the next frontier
  • LLM are already used in cedision making (experiment design, game etc.)
  • ICRL is less developed than ICSL

• Decision making agentsmust posses

  • generalization : required for supervised learning
  • exploration : making suboptimal decision to gather more information
  • planning : account long-term consequences of decisions
  • exploration is focused in this paper

• recent papers about ICRL

  • ICRL in transformer when they are explicitly trained
  • training is hard
  • in that case, Does it exhibit the capability to explore in-context?

• Deploying LLM to solve multi-armed bandit problem

  • classical RL problem shows the tradeoff between exploration and exploitation
  • this would be the building block to general RL question

• evaluate the in-context behavior

  • tested GPT-3.5, GPT-4, LLaMA2

  • only single configuration (prompt + model) showed satisfactory exploratory behavior

  • all failure is due to suffix failure (fails to select the best arm even once after some initial rounds)

    

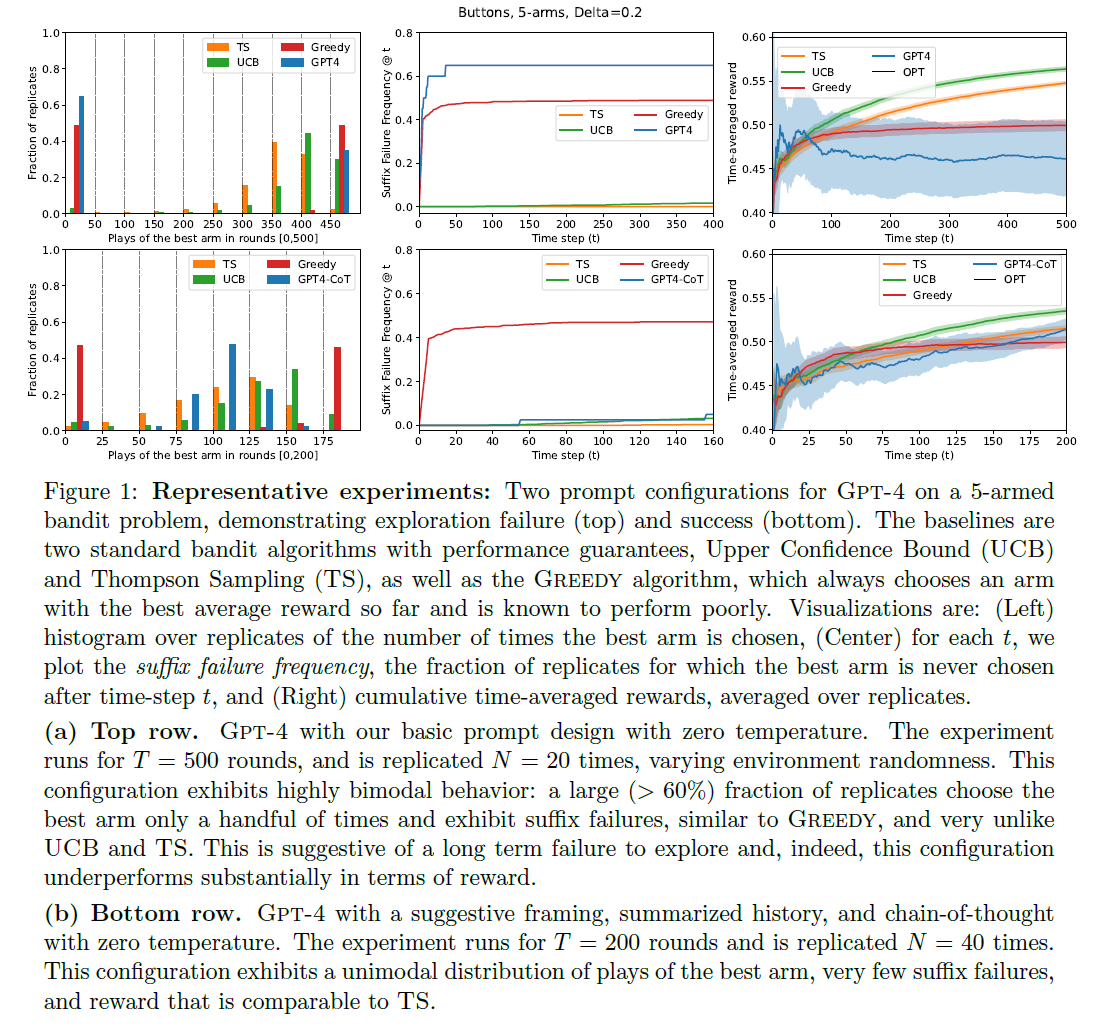
  • GPT-4 with basic prompt failed in over 60%

  • another failure is for LLM to behave uniformly

• successed configuration

  • GPT-4 + enhanced prompt

    • suggestive hint
    • summarizes the history of interaction into per-arm average
    • zero-shot CoT

  • SOTA model has capability to robustly explore if prompt is designed carefully

  • but it may fail in complex environments

    • summarizing history is non-trivial problem

• In-Context bandit learning is hard

  • stochasticity in the environment demands high-degree of replication for statistical significance
  • even single experiment involve hundreds or thousands LLM queries

• identify surrogate statistics as diagnostics for long-term exploration failure

  • characterize long-tern exploration failure

2. Experimental Setup

Multi-armed bandits

• used MAB variant, Stochastic Bernoulli bandits

  • $K$ possible actions (arms) $[K] = \{1, ... , K \}$
  • each arm $a$ is associated with mean reward $\mu_a \in [0, 1]$ (unknown)
  • an agent interacts with the environment with $T$ time steps
  • each time step $t \in [T]$ the agent selects an arm $a_t \in [K]$ and receives a reward $r_t \in \{ 0, 1 \}$ drawn from Bernoulli with mean $\mu_{a_t}$
  • the MAB instance is determined by the mean rewards and the time horizon

• reward for each arm is not chosen by the agent are not revealed $\rightarrow$ exploration is necessary to identify the best arm

• focus on MAB with the best arm has mean reward $\mu^* = 0.5 + \Delta / 2$ and all other arms has mean reward $\mu = 0.5 - \Delta / 2$

  • $\Delta = \mu^* - \mu$

• set $K = 5$ and $\Delta = 0.2$ as 'hard' instance

• set $K = 4$ and $\Delta = 0.5$ as 'easy' instance

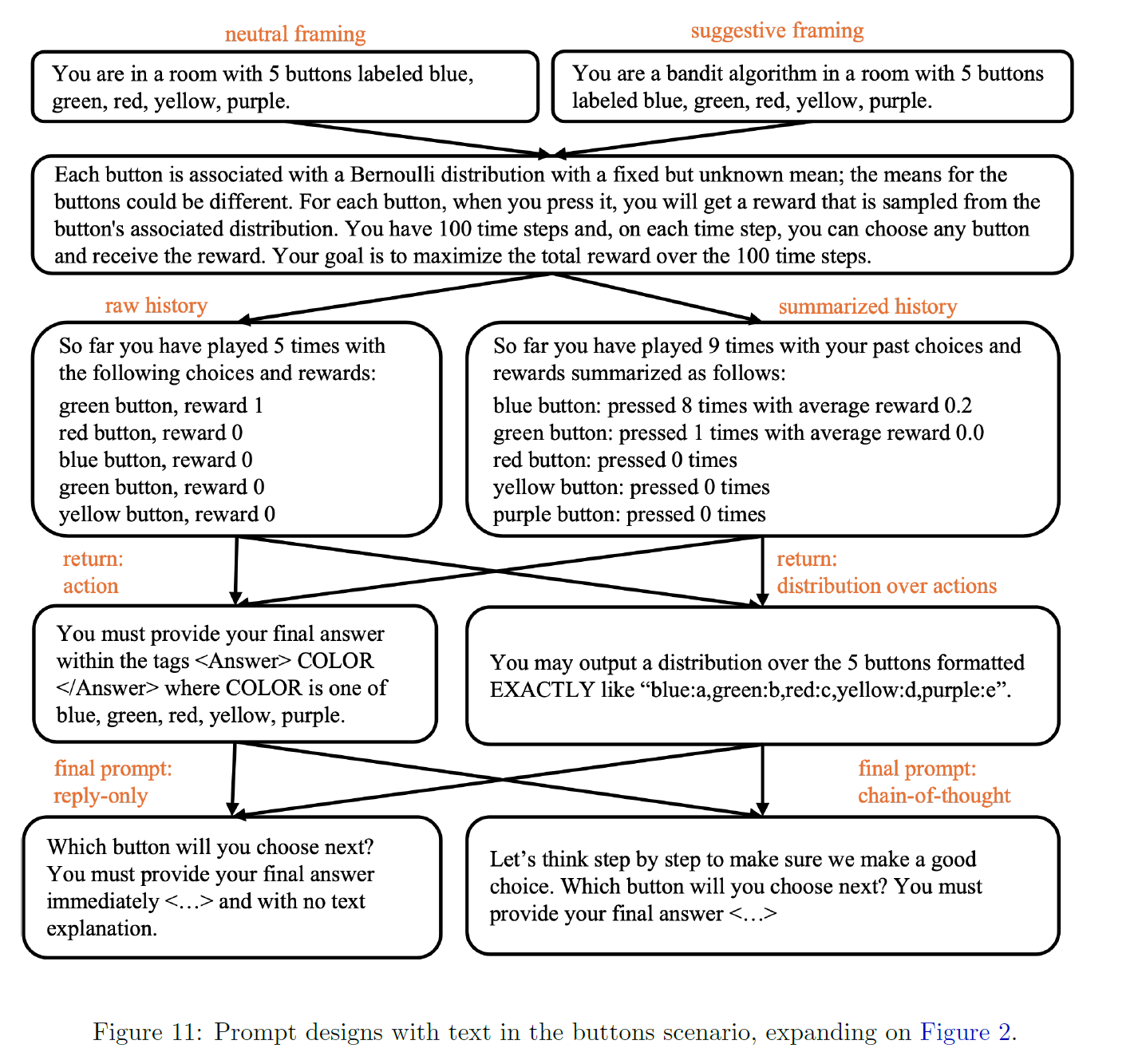
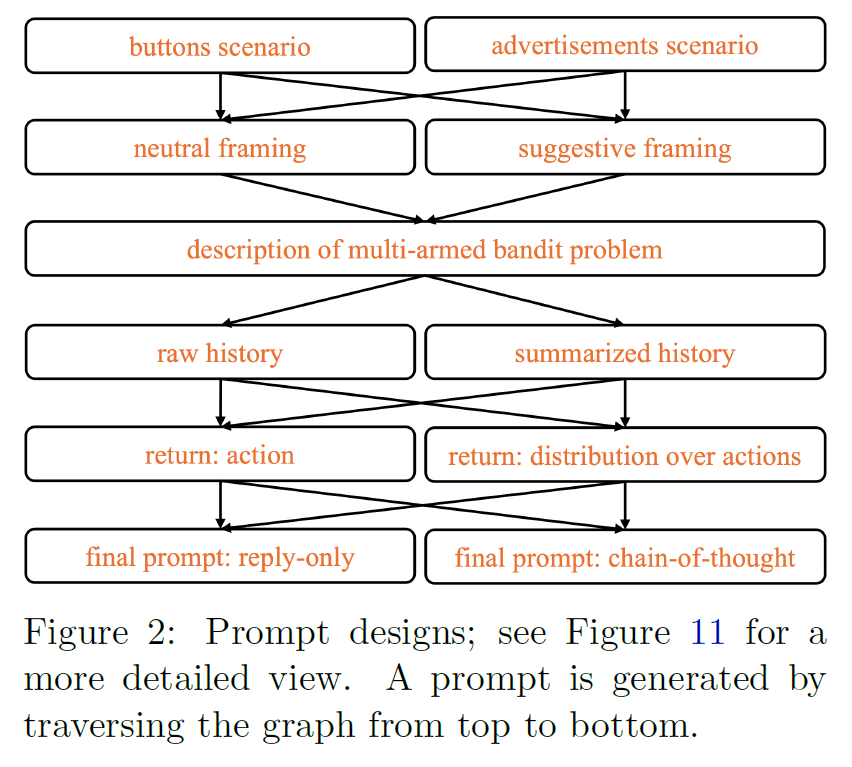
Prompts

• prompt design

  • scenario

    • positioning LLM as an agent choosing buttons to press
    • or a recommendation engine displaying advertisements to users

  • framing

    • suggestive of the need to balance exploration and exploitation
    • neutral

  • history

    • raw list over rounds
    • summarized via number of rounds and average rewards of each arm

  • requested final answer

    • single arm
    • distribution over arms

  • method

    • the answer only
    • CoT

  • 

  • basic prompt is buttons / neutral framing / raw history / return only arm / no CoT

• Each modification might help LLM with model's knowledge
  • advertising scenario / suggestive framing (system message) : model's knowledge of bandit algorithms
  • history summarization (user message) : if LLM reliably summarize history itself
  • returning a distribution (system message) : help to identify a good distribution (fails to sample from it)
  • CoT (system message) : general performance
• in GPT-4, used reinforced CoT design to additionally reminds the model to use CoT at user prompt

LLM configurations

• models
  • GPT-3.5-Turbo-0613
  • GPT-4-0613
  • LLaMA2-13B-CHAT with 4bits
• Temparature 0(deterministic) or 1
  • don't consider temp 1 with 'return distribution' as it may causes external randomness
• 5-letter $L_1 L_2 L_3 L_4 L_5$ notation for prompt design
  • $L_1$ : $\text{B}$ or $\text{A}$ for buttons or advertisements scenario
  • $L_2$ : $\text{N}$ or $\text{S}$ for neutral or suggestive framing
  • $L_3$ : $\text{R}$ or $\text{S}$ for raw or summarized history
  • $L_4$ : $\text{N}$ or $\tilde{\text{C}}$ or $\text{N}$ for CoT, reinforced CoT or No CoT
  • $L_5$ : $0$, $1$ or $\text{D}$ for temperature and returning a distribution (temp 0)
  • $\text{BNRN0}$ as a basic prompt
  • advertisement scenario will be used ads robustness check
• 48 configs for GPT-3.5 and LLaMA2 and 72 configs for GPT-4

Baselines

• two standard MAB algorithms

  • UCB
  • Thompson Sampling (TS)

• Greedy (doesn't explore and finally fail)

• no parameter tuning

• 1000 replicates for each baseline and each MAB instance

Scale of the experiments

• time horizon $T = 100$

• $N \in \{ 10, 20 \}$ replicates for each LLM configuration and bandit instance

• single experiment on GPT-4 with basic configuration for $T = 500$ for robustness check

• in detail

  • GPT-3.5

    • $N = 20$ replicates across all 48 prompt
    • about 200K queries

  • GPT-4

    • $N = 10$ replicates across 10 representative configurations

  • GPT-4 (additional aubustness check)

    • $T=200$
    • two for $N = 20$
    • two for $N = 40$

  • LLaMA2

    • free from query (local model)
    • hard MAB instance, 32 configs, $N = 10$

• $N \times T$ LLM queries for each config and MAB instance

  • $N$ : significance level, must be large to overcome randomnes,nms in reward
  • $T$ : effect size, must be large so that good algorithms have enough time to identify the optimal arm

• Both exploration failures are less frequent in easier MAB instances

• To cover extremely large prompt space, use small $\Delta$ and large $N$, $T$

• $N \in \{10, 20 \}, T = 100$ and $\Delta = 0.2$ do not provide enough statistical power to distinquish between successful and unsuccessful methods

• rely on surrogate statistics which can be detected in current moderate scale rather than scale up

3. Experimental Results

3.1 Overview

• All but one LLM config failed to converge to the best arm with significant probability

• Suffix Failures

  • LLM never selects the best arm after a small number of initial rounds

• Uniform-like failures

  • LLM chooses all arms at uniform rate
    
  • failed to eliminate poorly performing arms
    

• the only one exception is GPT-4 with $\text{BSS}\tilde{\text{C}}0$

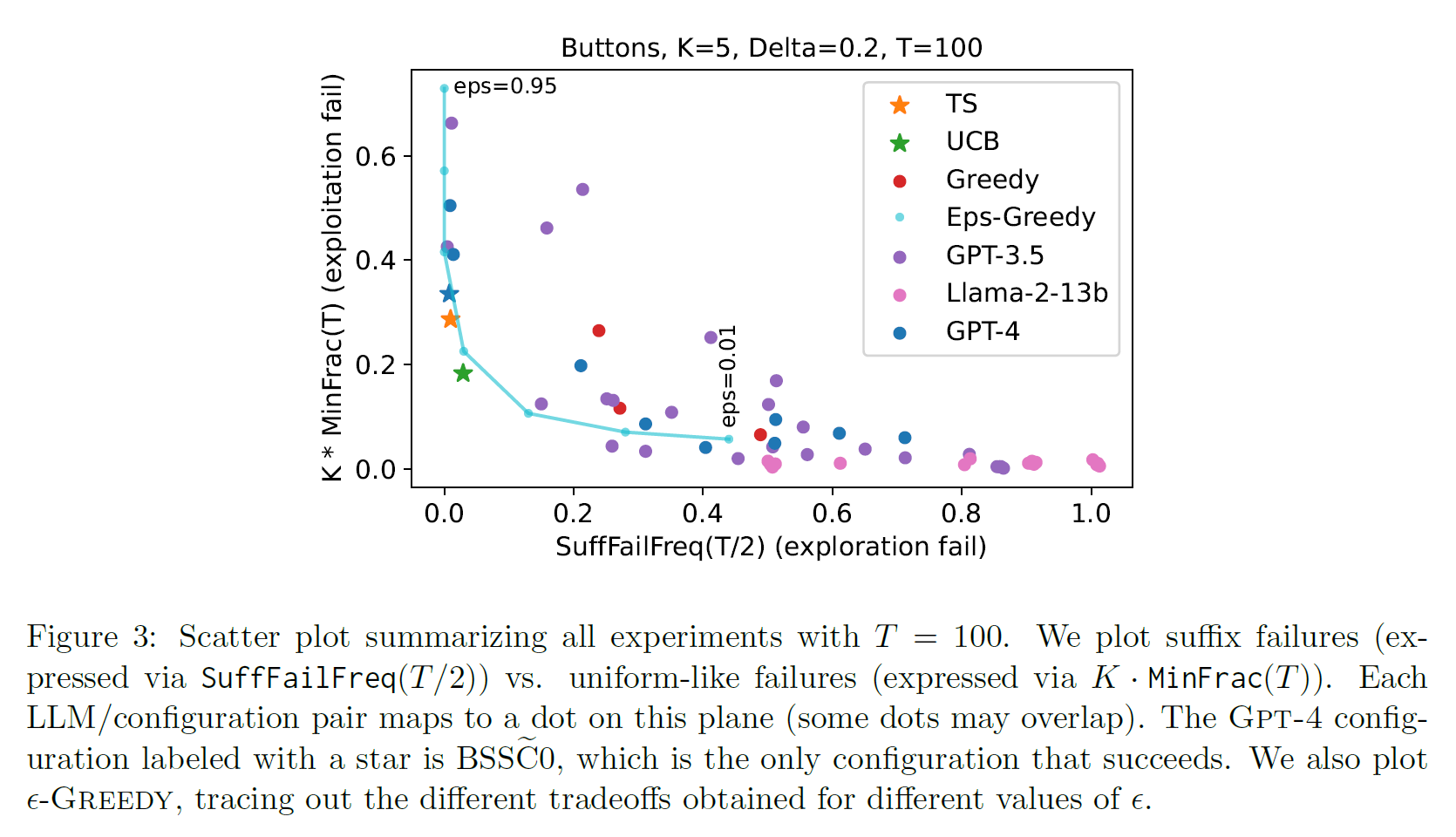
• Fig 3 : summarize the main set of experiments (hard MAB instance)

• two surrogate statistics

  • SuffFailFreq : measures suffix failures $\rightarrow$ exploration fail
  • $K \cdot$ MinFrac : measures uniform-like failures $\rightarrow$ exploitation fail

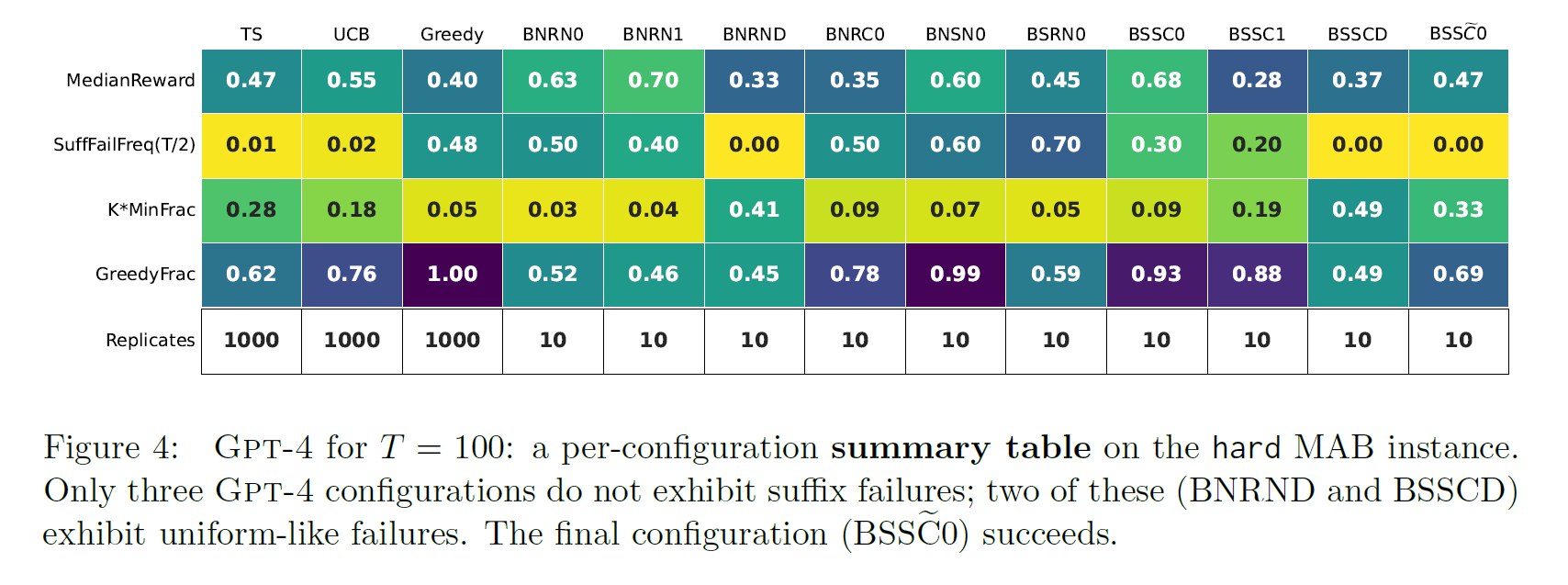
• show another statistic GreedyFrac (how similar a method is to GREEDY)

• only GPT-4 with $\text{BSS}\tilde{\text{C}}0$ follows the baseline TS and UCB
  

3.2 Identifying failures

• focus on GPT-4

Suffix Failures

• most of the LLM configs exhibit bimodal behavior

  • large fraction of the replicates choose the best arm very rarely
  • few replicates converged extremely quickly

• Consistent with this, suffix failures occurred many times
  

• suggests long-term failure to explore

  • cannot be improved by running more time steps
  • very similar to greedy and different from UCB and TS

• For an experiment replicate $\text{R}$ and round $t$

  • SuffFail($t, \text{R}$) = 1 if the best arm is never chosen in rounds $[t, T]$
  • SuffFailFreq($t$) = mean({SuffFail($t, \text{R}$) : replicates $\text{R}$)
  • SuffFailFreq($T/2$) : frequency of failure to choose best arm even after the last half rounds

• basic config (GPT-4-$\text{BNRN0}$) in Fig1 (top) for T = 500, Fig 5 for GPT-4 for T = 100

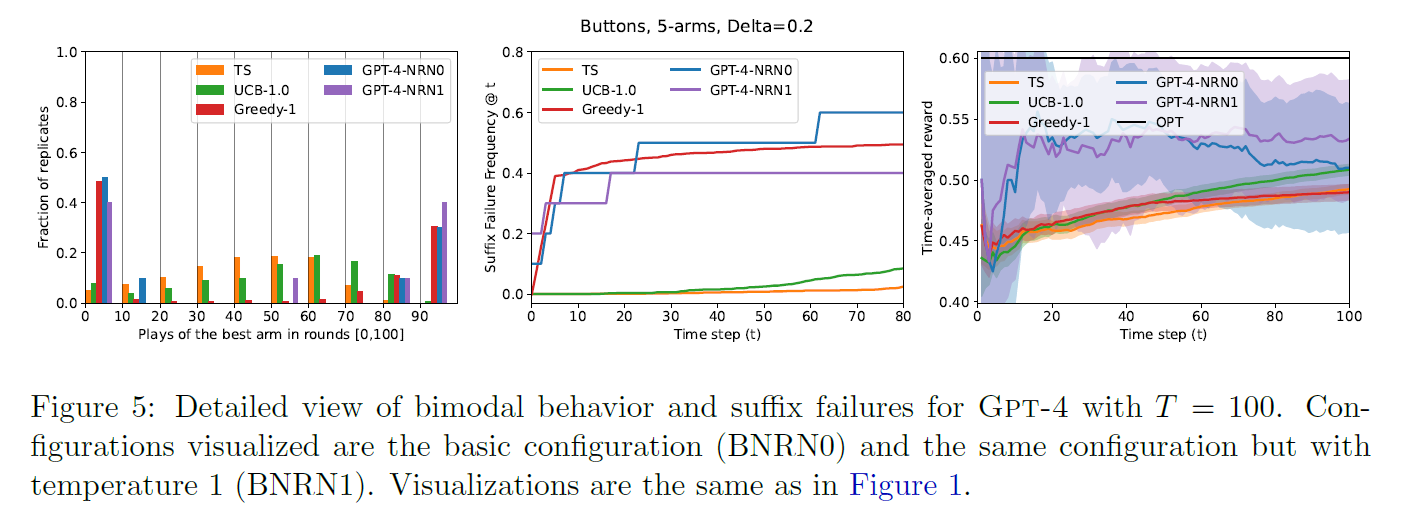
• bimodal behavior is shown in left plot

• LLMs have much higher SuffFailFreq than UCB and TS

• as T = 100 is not enough, suffix failures are not fully reflected in Fig 5 (right)

• in Fig 1, suffix failure makes the larger differences in reward for large $T$

Uniform-like failures

• in Fig 3 (left), 3 GPT-4 configurations avoid suffix failures

• two of these shows the uniform-like failures (exploitation failure)

• For an experiment replicate $\text{R}$ and round $t$,

  • $f_a(t, R)$ be the fraction of rounds in which a given arm $a$ is chosen
  • MinFrac($t, R$) =$\min_a f_a(t, R)$
  • MinFrac($t$) = mean({MinFrac($t, R$) : replicates $R$ })
  • MinFrac($t$) $\le 1/K$ for all $t$, rescale it by multiplying $K$
    i.e. $K \cdot$ MinFrac($t$)
  • Larger MinFrac($t$) means more uniform selection of arms at time $t$

• for LLMs, MinFrac($t$) doesn't decrease over time and stays larger than that of baselines
  

• for two GPT-4 that avoid suffix failures and get uniform-like failures, (BNRND, BSSCD) both used distributional output

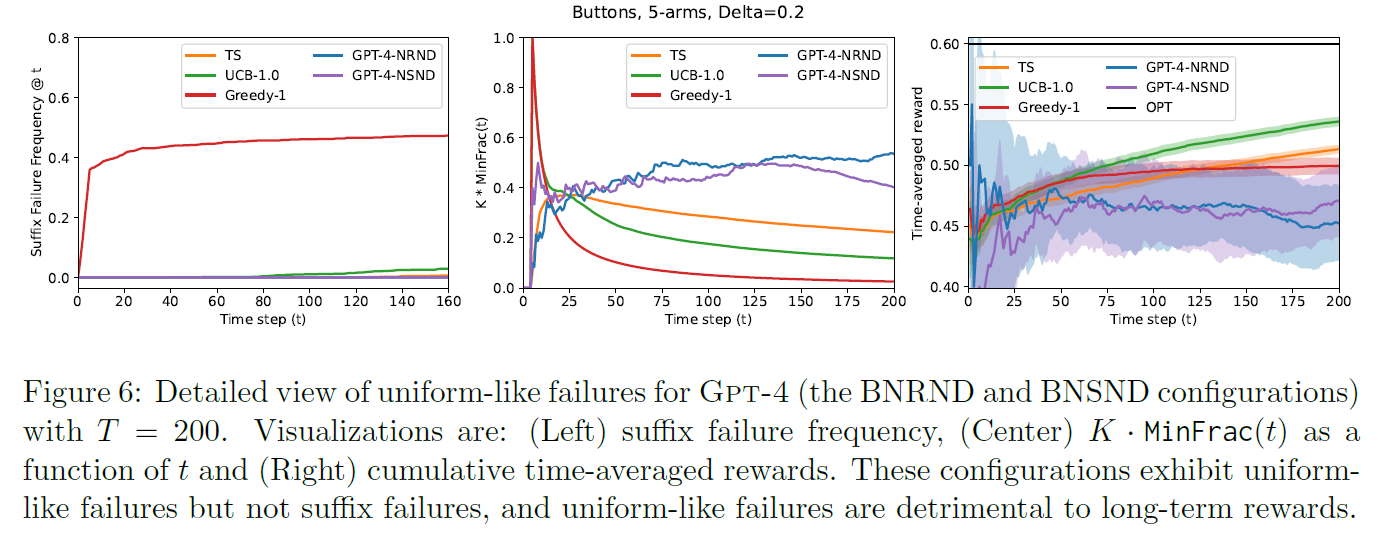
• MinFrac doesn't decrease while baselines does

• in longer $T$, it has much lower reward than baselines

  • poor long-term performance

Generality of the failures

• all LLMs except GPT-4-$\text{BSS}\tilde{\text{C}}0$ exhibit either a suffix failure or a uniform failure for hard MAB

• other experiments have similar result

• summary

  • GPT-4 performed much better than GPT-3.5

  • LLaMA 2 performed much worse

  • all LLMs are sensitive to small changes in the prompt design

    • different modification interact with each other

3.3 Investigating successes

• GPT-4-$\text{BSS}\tilde{\text{C}}0$

  • no suffix failures
  • $K \cdot$ MinFrac is slightly larger than TS
  • reward is compatible to TS

• ran this config on hard MAB with $T = 200$ and $N = 40$ + $\text{BSR}\tilde{\text{C}}0$ as an ablation
  

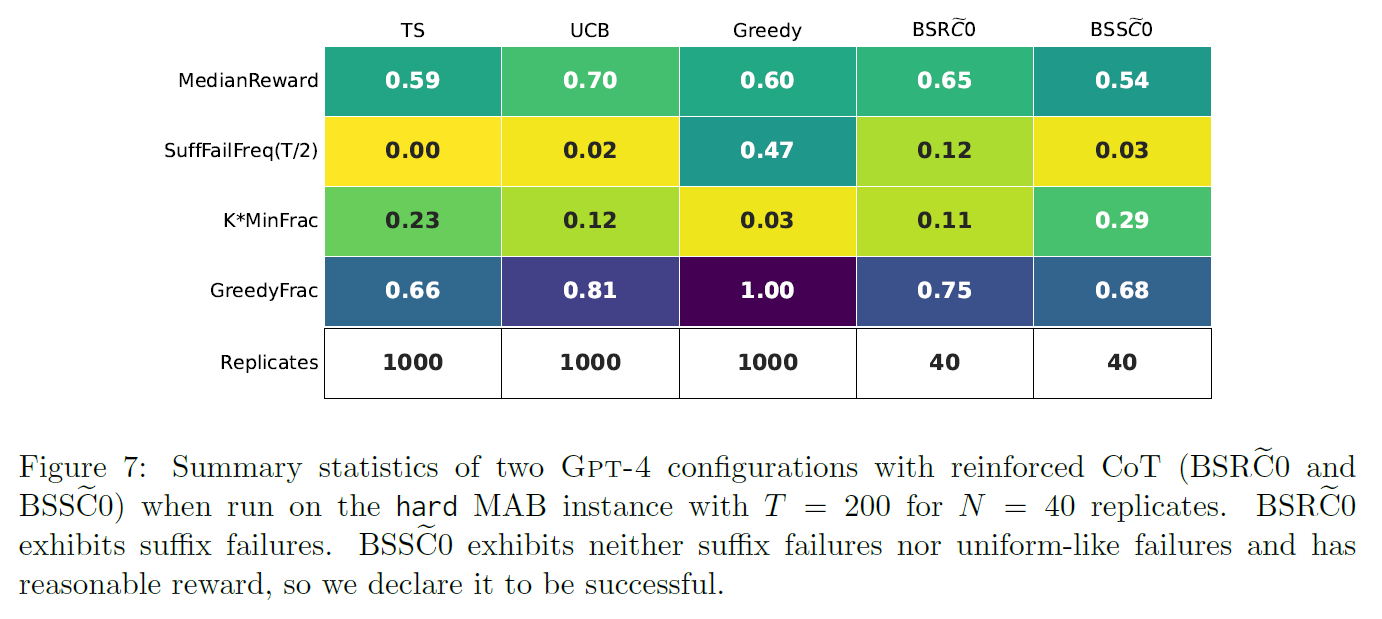
• $\text{BSS}\tilde{\text{C}}0$ worked well in longer T

• $\text{BSR}\tilde{\text{C}}0$ showed non-trivial fraction of suffix failures (Fig 1(b))

• Fig 8

  • basic config tends to commit to a single arm for several rounds (like greedy)
  • $\text{BSR}\tilde{\text{C}}0$ also commits for long periods but to a lesser extent than the basic config
  • $\text{BSS}\tilde{\text{C}}0$ switches arms requently and qualitatively appears much more similar to TS

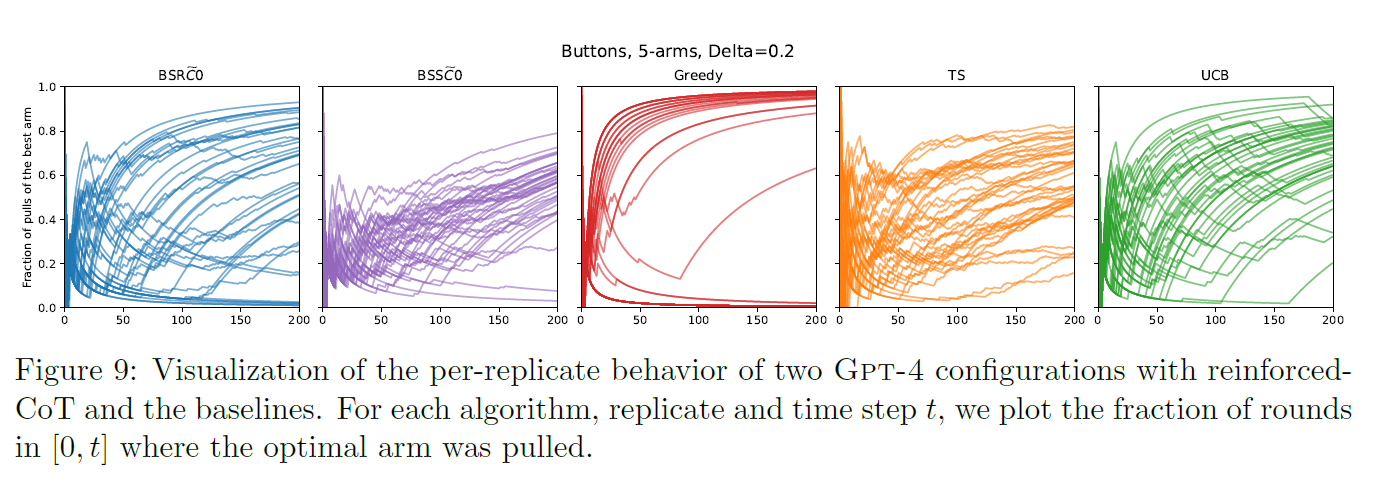
• Fig 9

  • plotted the fraction of rounds in $[0, t]$ where the optimal arm was pulled
  • $\text{BSR}\tilde{\text{C}}0$ looks like UCB except that sone runs shows suffix failures (goes to 0)
  • $\text{BSS}\tilde{\text{C}}0$ is similar to TS with almost all replicates slowly converge to 1

3.4 Root causes

• understand why LLMs behave like this

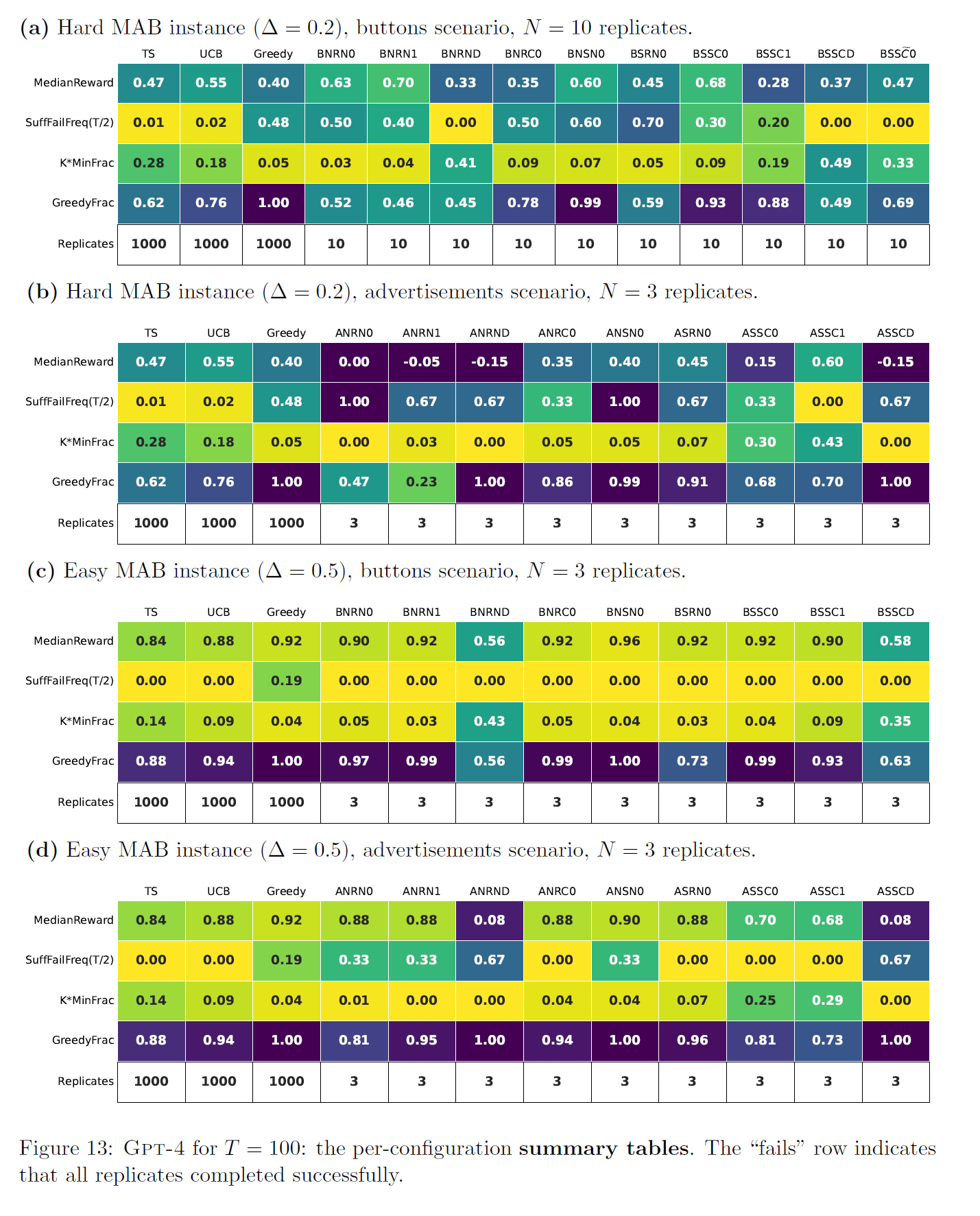
• Fig 13
  • with (a) and (c), GPT-4 shows qualitatively different behavior in easy and hard MAB
  • easy instance is much easier
  • in easy instance, GPT-4 showed very high GreedyFrac $\rightarrow$ behave like Greedy (as it performed quite well)
  • GPT-4 performs quite well in low-noise settings
  • in hard instance, GPT-4 did something non-trivial (neigher Greedy nor uniform)

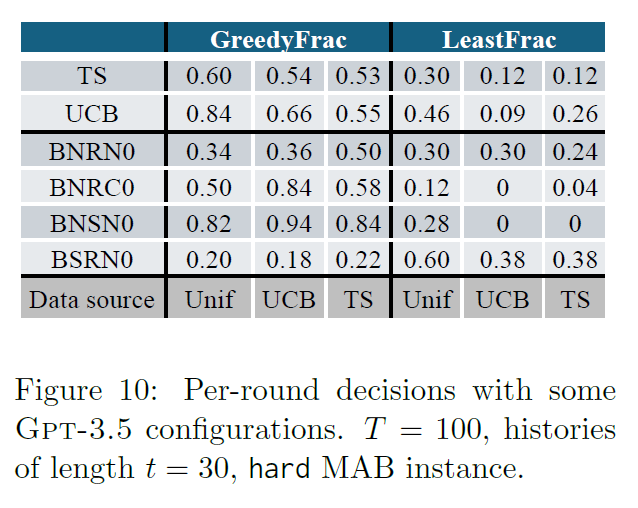
• Fig 10

  • per-round decisions with GPT-3.5

  • each experiment considers a particular distribution of bandit histories

  • sampled 50 histories of length $t$

  • tracked two statistics for each agent

    • empirically best arm so far vs a lesast-chosen arm so far

  • uniform sampled data + UCB and TS sampled data

  • per-round performance of both the LLMs and baselines is very sensitive to data source

  • $\text{BNSN0}$ is too greedy, $\text{BNRN0}$ is too uniform

  • $\text{BNRN0}$ and $\text{BNRC0}$ fall within the reasonable range by baselines while they failed in longitudinal experiments

  • hard to assess whether LLM agents are too greedy or too uniform based on per-round decisions

4. Related work

• LLM capability
  • general intelligence
  • causal reasoning
  • mathmatical reasoning
  • planning
  • compositionality
• In-context capabilities
  • theoritical and empirical investigation to ICSL
  • ICRL study focus on models trained from trajectory data from another agent
  • justify with Bayesian meta-reinforcement learning perspective
  • transformers work like TS and UCB
• applying LLM to real-world decision making
  • gaming, programming, medicine
  • generative agent to simulate human behavior in open-world environment
  • LLM-enabled robots
• LLM performance in a task that characterizes intelligent agents with two-armed bandits
  • very easy MAB ($K = 2$, $\Delta = 0.6$)
  • single prompt design
  • compared to human
  • GPT-4 performed well

4.1 Further background on MAB

• UCB
  • explores by asigning each arm $a$ an index (average reward + bonus)
  • choose the arm with largest index
  • bonus form $\sqrt{C/n_a}$ and used $C = 1$ for this paper
• TS
  • proceeds as if the arms' mean rewards were initially drawn from some Bayesian prior
  • computes a Bayesian posterior using the given history
  • chooses an arm with largest mean reward
  • chose prior that uniformly draws the mean reward at random from [0, 1] in this paper
  • update each armindependently as a Beta-Bernoulli conjugate prior
• regret
  • difference in expected total reward of the best arm and the algorithm
  • baselines achieve regret $O(\sqrt{KT \log T})$ which is nearly minimax optimal for $K$ and $T$
  • achieved also $O(\sqrt{{K \over \Delta} \log T}$ for instance-optimal regret rate
• $\epsilon$-greedy and greedy

5. Discussion and open questions

• contemporary LLMs do not robustly engage in exploration required for basic statistical RL and decision making problems without further intervention

Basic interventions and the need for methodological advancements

• Experiment with other prompts

• Experiment with few-shot prompting

• Train the LLM to use auxilary tools

Implications for complex decision making problems

• simple MAB provides a clean and controllable setup

• in more complex RL and decision making, similar failures also occur

• the solution for MAB may not generalize to more complex settings

• even for linear contextual bandits, this approach may not be applicable without a substancial intervention

6. Comment

ICSL이 아닌 ICRL의 관점에서 LLM이 어느 정도의 지식을 가지고 있는지 확인하는 논문. 단순한 문제이긴 하지만 요즘 LLM Agent에 대해서도 연구가 이뤄지는 만큼 Baseline이 되긴 할듯. RL에서는 단순한 문제지만 GPT-4에서 프롬프팅을 섞어야 해결이 가능할 만큼 LLM 능력으로는 접근하기 쉽지 않은듯