1. Introduction

• LLMs' reasoning capabilities are elicited by prompting techniques
  • Few shot prompting with intermediate steps augmented demonstration exemplars
  • Zero shot prompting with specific instructions to show intermediate steps
• Can LLMs reason effectively without prompting?

  • there exists a task-agnostic way to elicit CoT reasoning by altering the decoding procedure
    
    

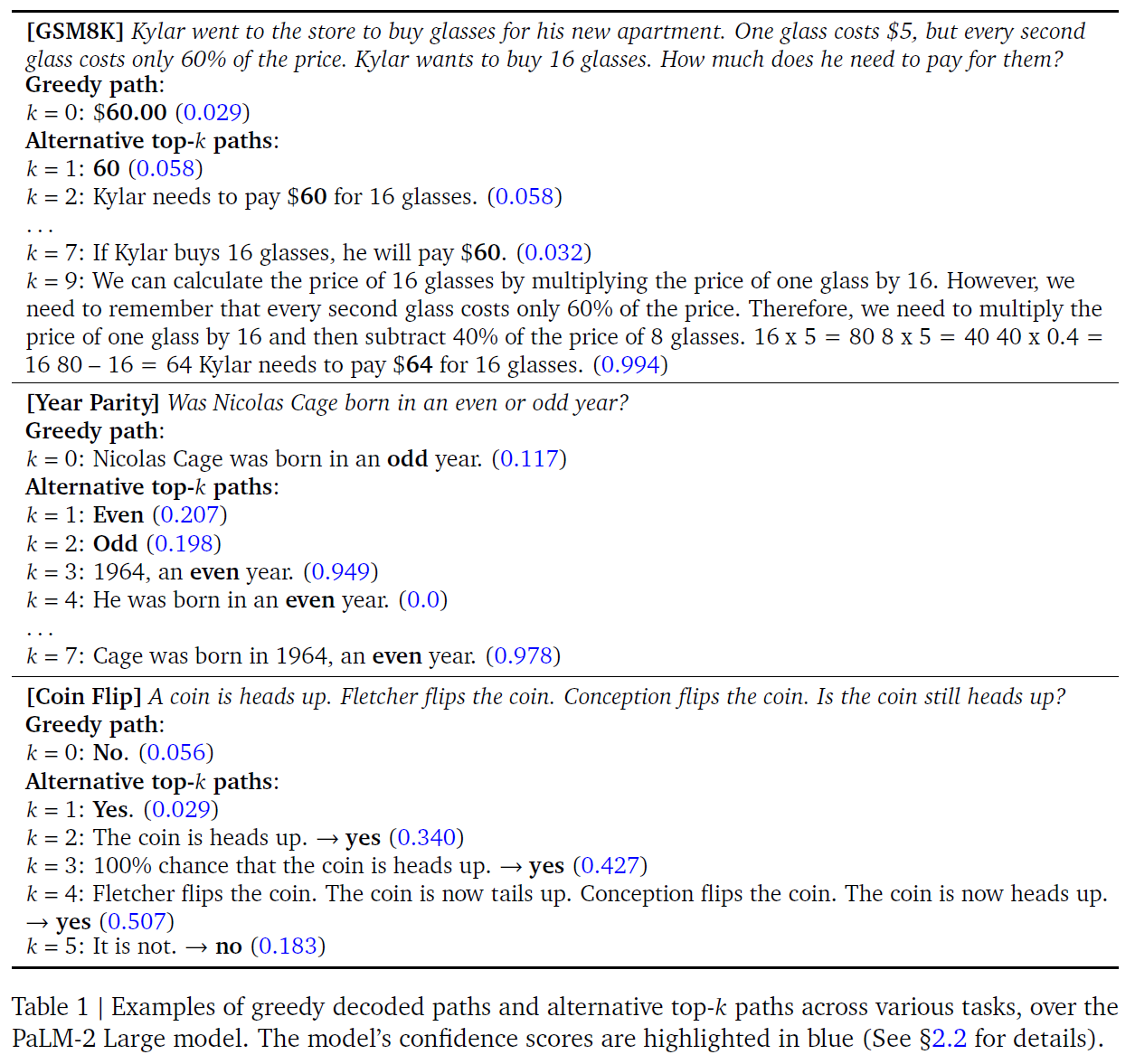
  • LLM generates a wrong answer via the standard greedy decoding but there are alternative top-k token inspection unveiled inherent CoT paths

    • Use standard QA format
    • LLMs struggle with reasoning when relying solely on greedily decoded paths
    • CoT reasoning patterns emerge naturally within the alternative paths among the top-k tokens
    • when CoT path is present, the model demonstrates increased confidence in the final answer
    • CoT-decoding : a method to sift through the top-k paths by isolating the most reliable paths

  • CoT decoding elicits reasoning capabilities without explicit prompting

    • enhances the model's reasoning capabilities
    • paths are more prevalent in tasks frequently represented in the pre-training data and less tso in complex, synthetic tasks $\rightarrow$ Still prompting is needed

• Summarized Contributions
  • LLMs inherently possess reasoning capabilities
  • they generates CoT reasoning when examining alternative top tokens
  • mere change in decoding strategy effectively elicit model reasoning
  • LLM's confidence in its final answers increases when CoT is in its decoding path
  • CoT decoding to select more reliable decoding paths

2. CoT Decoding

2.1 The presence of CoT Paths during Decoding

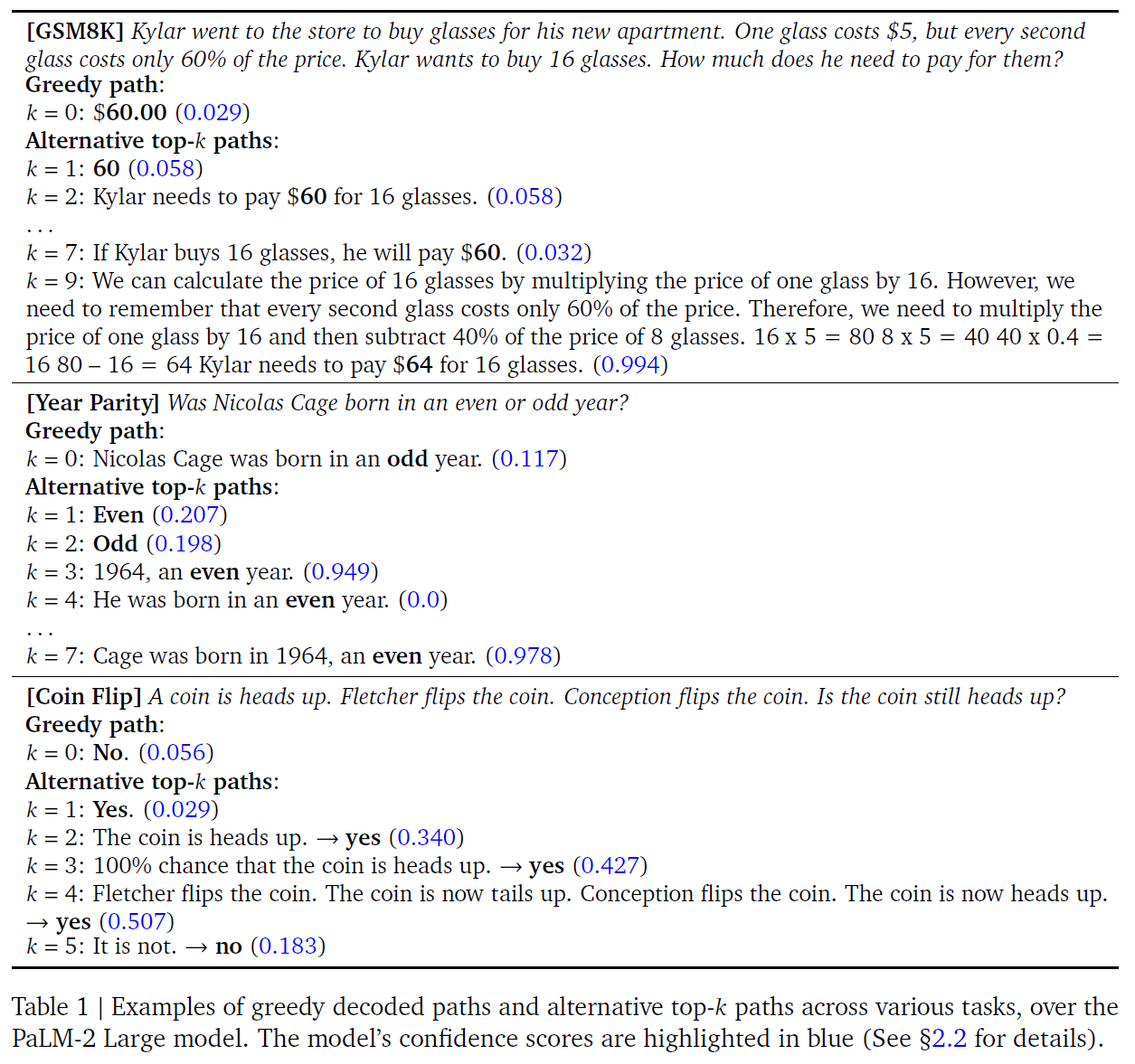
• $k$ represents the coice of the $k$-th token at the first decoding step

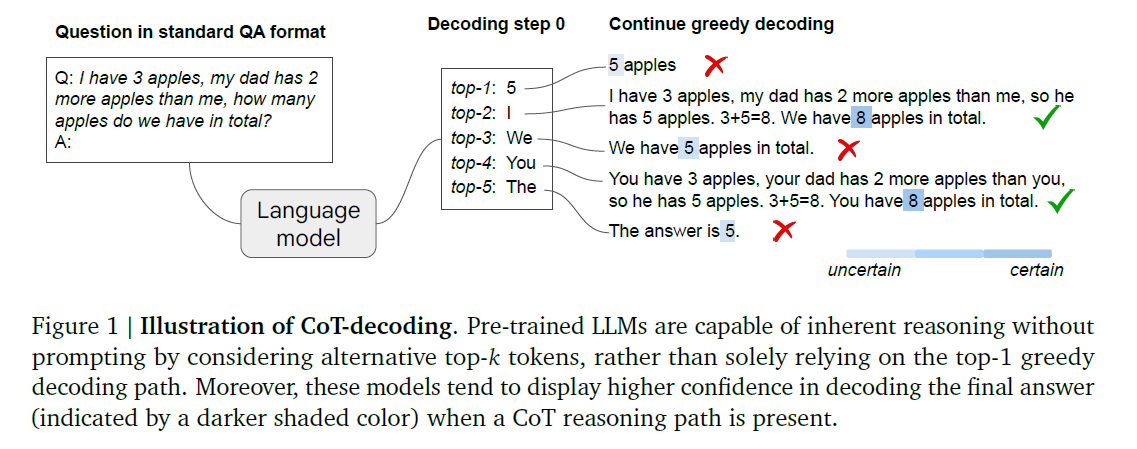
• PaLM-2 Large model example

• The greedy decoding often doesn't contain CoT

  • model's skewed perception of problem difficulty
  • pretrained on simpler questions

• direct answer prompts generally result in low accuracy

2.2 CoT-Decoding for Extracting CoT Paths

• Extracting CoT paths from the top-$k$ decoded paths is an issue

  • CoT Paths don't consistently outrank non-CoT in the model's probability assessment
  • they often don't represent the predominant answer among all paths $\rightarrow$ Self-consistency is not applicable

• the presence of CoT path typically leads to a more confident decoding of the final answer

  • characterized by a probability disparity between the top and secondary tokens

  • $\Delta_{k, \text{answer} } = {1 \over n} \sum_{x_t \in \text{answer}} p(x_t^1 \ | \ x_{<t}) - p(x_t^2 \ | \ x_{<t})$

  • $x_t^1$, $x_t^2$ means the top two tokens at each decoding step $t$ in the $k$-th decoding path chosen for their maximum post-softmax probabilities from the vocab

  • Overall confidence in decoding the final answer is approximated by averaging the probability differences for all relevant $x_t$ tokens

    • For the GSM8K question in Table 1, average the probability differences for '6' and '0'

  • Called CoT-Decoding and aimed to extract CoT Paths

  • CoT path shows high $\Delta$ value

• Additional heuristic about the length of the answer

  • longer decoding paths more likely contain CoT
  • general applicability is limited
  • Normalize the probability score by length $\rightarrow$ intruduces a length bias (when the decoding paths are of similar lengths, its effectiveness diminishes)

Identifying the answer spans

• for math tasks, one can extract the last numerical value

  • less precise when there are distractive numbers/options and open-ended responses

• extending the model's output with the prompt "So the answer is"

  • only token ids are needed
  • suitable for encompassing mathematical and natural language reasoning
  • crucial to calculate $\Delta$ over the answer spans from the original decoding path, not those following "So the answer is"

• When answer is more open-ended, modify the $\Delta$ calculation

  • If the options are defined, aggregating the probability mass over "yes" and compute the probability differences between the aggregated mass on "yes" and "no"
  • addressing this limitation is left for further research

Branching at other decoding steps

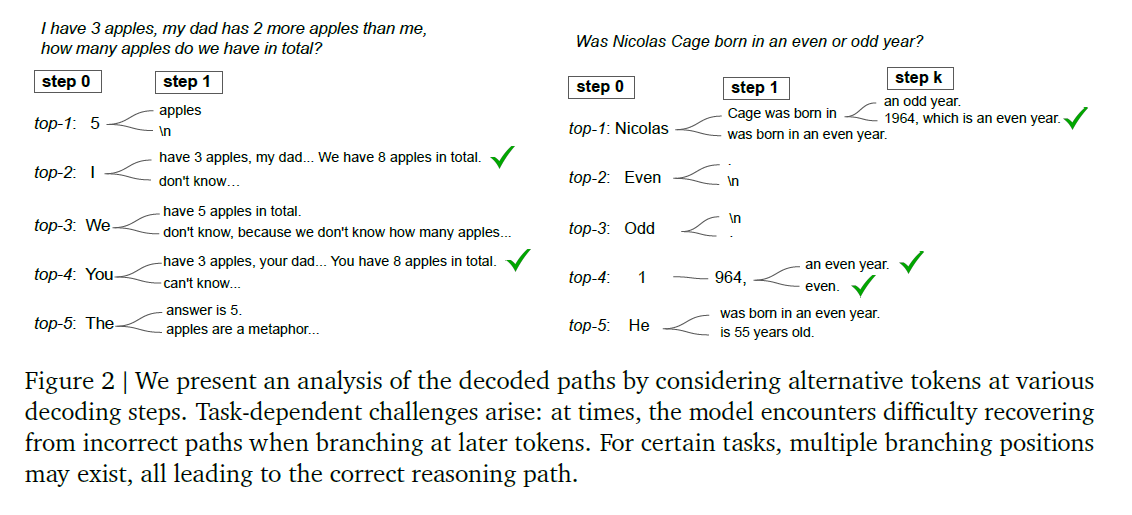
• Is branching viable at later decoding stages?

• Early branching significantly enhances the diversity of potential paths

• Optiman branching point may vary with the task

  • for year parity task, mid-path branching can effectively yield correct CoT paths

Aggregation of the decoding paths

• Aggregate the answers over all those paths like self-consistency without CoT prompting

  • to mitigate sensitivity to small differences in the model's logits particularly when relying solely on the path with the maximum $\Delta$

• Majority answer may not be correct

• weighted aggregation method

  • take the answer that maximizes $\tilde{\Delta}_a = \sum_k \Delta_{k, a}$
  • $\Delta_{k, a}$ means the $k$-th decoding path whose answer is $a$
  • this enhances the stability of the results

Sampling under the standard QA format

• Can sampling achieve a similar effect and unveil the CoT reasoning paths?

• althouth sampling works well under few-shot CoT prompting, it doesn't exhibit the desired behaviour when the model is queried with the standard QA format

• less than 30% of the sampled responses contain a correct CoT path

• the model tends to provide a direct answer as the first token is sampled based on the model's probability distribution reflecting the model's tendency to output direct answer

• the rest of the tokens lead to incorrect final answers

3. Experiments

• Used standard QA format (Q: (question)\nA:)
• $k=10$ as default
• PaLM-2 with different scales
• Mistral-7B
• last numerical numbers or the available options for Mistral
• extend the output with "So the answer is" for PaLM-2

3.1 Mathematical Reasoning Tasks

• GSM8K (grade-school math problems)
• MultiArith (multi-step arithmetic dataset)

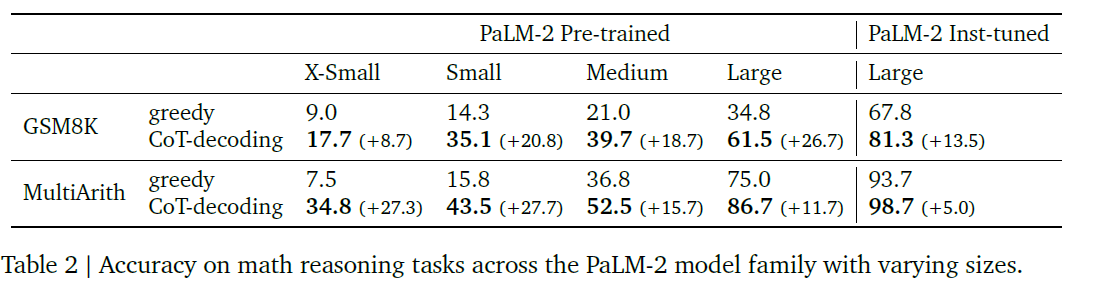
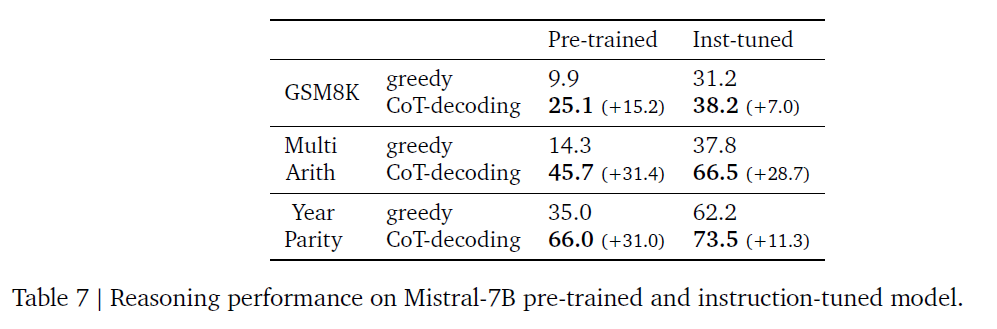
• CoT Decoding significantly enhances models' reasoning ability

• CoT Decoding partially closes the gap between the pre-trained model and instruction-tuned model

• Instruction Tuning with sufficient CoT data can also be partially achieved by CoT Decoding

• As instruction-tuning contains the CoT annotations, the model is expected to generate inherently generate CoT paths

• Even after instruction-tuning, the model occasionally attempts to directly address a question

Scaling results and choice of $k$

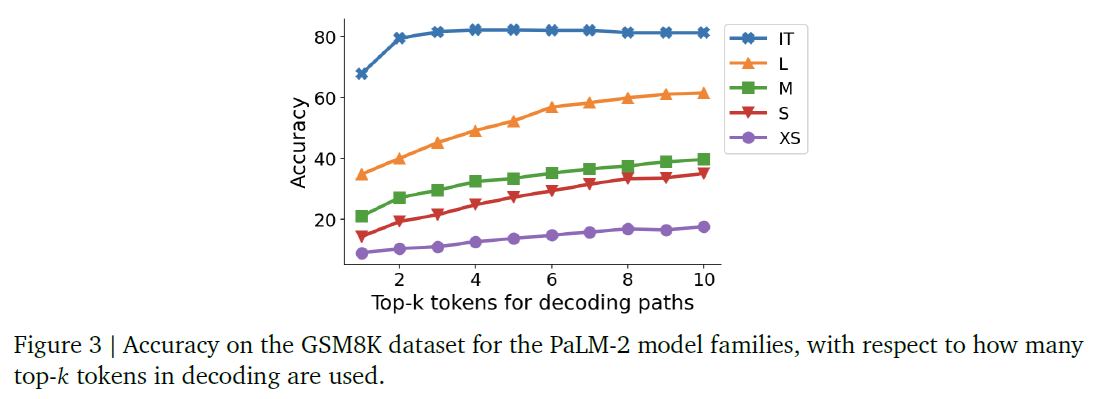
• higher $k$ typically result in improved model performance

  • correct CoT paths are often ranked lower

• for IT models, the effect of $k$ is not significant

  • instruction-tuning brings forth the majority of CoT-paths to the first few paths

3.2 Natural Language Reasoning Tasks

• year parity task : Was (person) born in an even or odd year?
• Even SoTA models like GPT-4 achieves at-chance accuracy (~50%) when prompted directly
  • SoTA LLMs are perfect for retrieving the year or judging the parity given the correct year
  • the limitation lies in the model's ability in knowledge manipulation
• 100 celeb names and their birth years

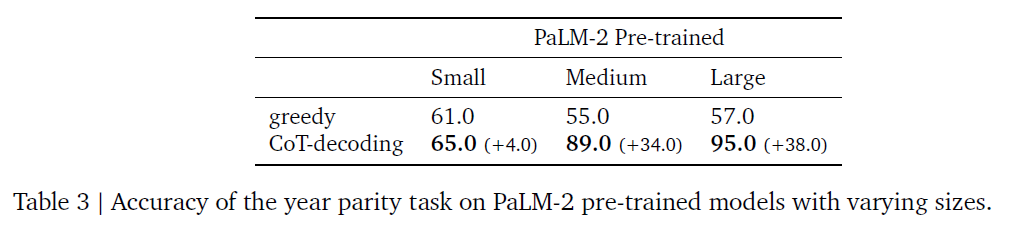
• When the model is small, the model becomes incapable to determine the parity even given the correct year
  • the performance doesn't vary significantly for model sizes below "Small" size

3.3 Symbolic Reasoning Tasks

• Coin Flip with 2, 3, 4 rounds of potential flip

• two tasks from Big-Bench-Hard

• Web of lies with 3, 4, 5 truth/lie statements

• Multi-step arithmetic with variuous depth and length (generated)

• existing dataset from (Suzgun et al., 2022)

• Sports understanding and Object Counting from Big-Bench

The presense of correct CoT paths depends on the taks prominence in the pre-training distribution

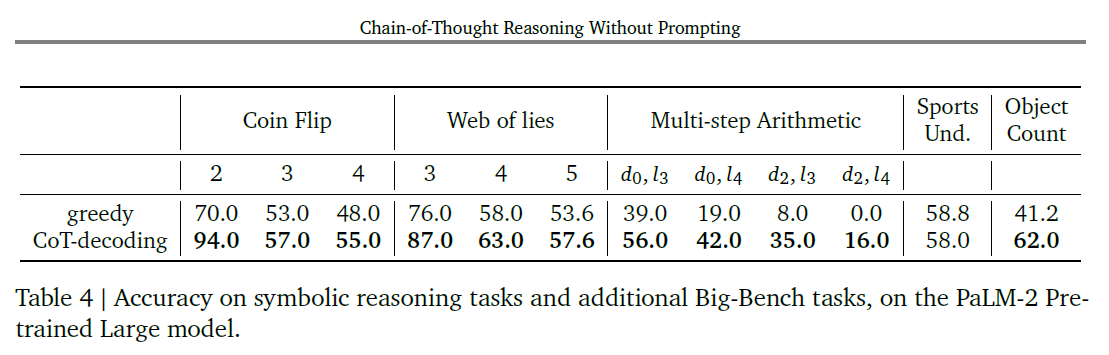
• CoT-Decoding gain is decreasing when the task complexity increases

• When task is highly synthetic, the model cannot generate correct CoT paths

  • tasks that lack significant representation in the pre-training distribution
  • tasks that require accurate state tracking (Coin-Flip and Web-of-Lies) $\rightarrow$ easily lose track of the states as the task became more complex
  • Multi-step Arithmetic and Object counting
  • CoT prompting based techniques can 'teach' how to solve tasks like above

Compared to CoT Prompting

• the aggregated path approach significantly improves the accuracy compare to taking the maximum path only

• the aggregated path results in a similar performance to few-shot CoT

  • model possesses intrinsic abilities in solving this task effectively

• CoT prompting takes the intrinsic CoT path to the top-1 path

• CoT Decoding exhibits a more 'free-form' generation in comparison to alternative CoT prompting

  • encourage the diversity at the initial decoding step
  • absence of explicit constraints imposed by prompt

• CoT Decoding can reveal what LLMs' intrinsic strategy in solving a problem without being influenced by the prompts

  • Few shot CoT follows the standard method of solving this task (profession - evaluation)
  • influenced vby the few-shot prompt

3.4 Results across Model Families

• CoT path emerges too

• consistent improvements across model families

4. Conclusion

• inherent capabilities of LLMs in generating CoT paths

• exploring alternative top-k tokens reveals the natural existence of reasoning paths

• presence of a CoT path correlates with increased model confidence in decoding its final answer

• additional computational costs

  • future work may leverage the CoT paths to fine-tune the model

• focused on branching at the first token

  • one can explore branching at any token and find best possible paths
  • how to reliably identify the best token during the search

5. Comment

확률이 가장 높은 토큰이 아니라 나머지 Top-k 중에 자연적인 CoT가 적용되어 정답을 찾는 Path가 있을 것이라는 굉장히 발상적인 아이디어. 계산량을 제외하고 봤을때 가장 참신한 아이디어였던 것 같음. 항상 Greedy가 옳은가에 대해 돌아볼 수 있는 논문.