1. Introduction

• To enhance LLMs' capability to reason and solve complex problems via prompting

  • Few-shot & Zero-shot CoT $\rightarrow$ how humans solve problems step-by-step
  • decomposition based prompting $\rightarrow$ how humans breakdowns problems into subproblems
  • step-back prompting $\rightarrow$ how humans reflec on task nature to derive general principles

• Each method serves as an atomic reasoning module making an implicit prior assumption of the process on how to tackle a given task

• Instead, each task has a unique intrinsic structure underlying the reasoning process involved in solving it efficiently

  • Least-to-Most Prompting is more effective than CoT at symbolic manipulation and compositional generalization due to the decomposition structure of the tasks

• Self-Discover $\rightarrow$ how humans devise areasoning probram for problem-solving

  • Aims to discover the inderlying reasoning structure of each task
    
    

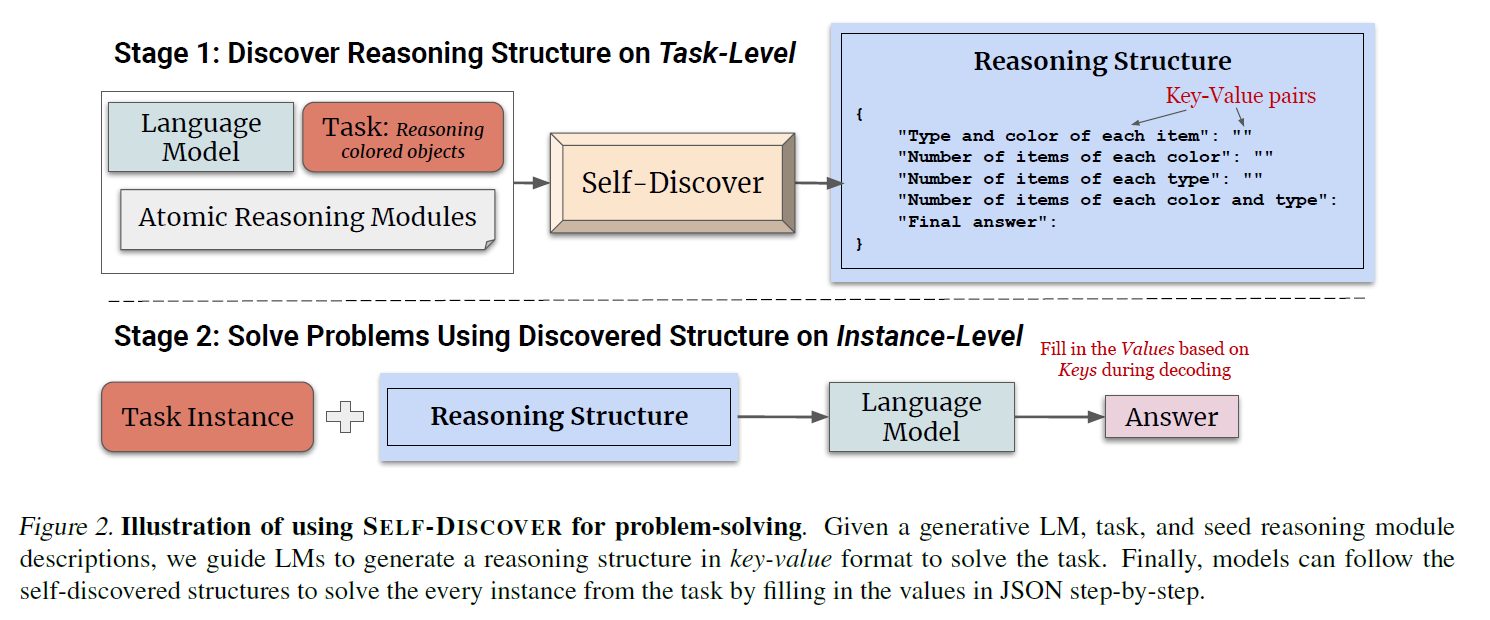
  • It composes a coherent reasoning structure intrinsic to the task (Stage 1)

    • Operates at Task Level
    • uses three actions to guide LLM to generate a reasoning structure for the task

  • Solves instances of the task using the discovered structure (Stage 2)

    • LLM simply follows the self-discovered structure to get the final answer

• Self-Discover helps to use multiple atomic reasoning modules like CoT

• It only needs 3 more inference steps on the task-level (more performant than inference-heavy ensemble approaches like self-consistency)

• It conveys LLMs' insights about the task in a more interpretable way

• Tested 25 challenging reasoning, it outperformed 21/25 tasks

  

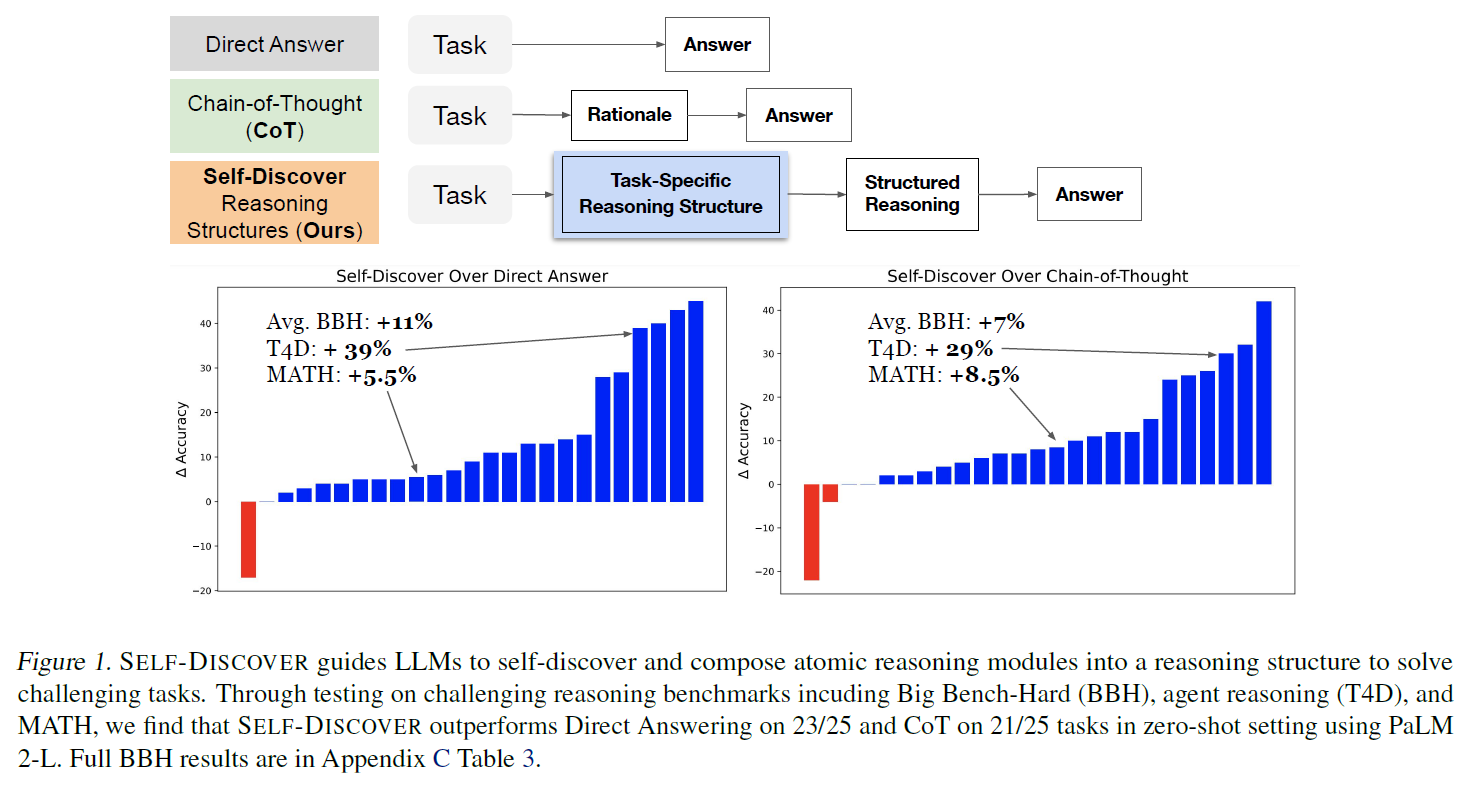
  • It achieves superior performance against a inference-heavy method like SoT + Self-consistency and Majority voting

• Compared Self-Discover with prompts optimized using a training set

  • Performed par or better than OPRO

• Analyzed its effectiveness by breaking down BBH task into 4 categories

  • Self-Discover worked best on tasks requiring world knowledge
  • it has a moderate performance boost on algorithmic tasks compared to CoT

• Error analysis on MATH

  • majorities of failures comes from computation errors
  • showed the universality of the reasoning structures by PaLM2 to GPT-4 / GPT-4 to Llama-2-70B

2. Self-Discovering Reasoning Structures for Problem-Solving

• How humans use prior knowledge and skills to devise a reasoning program

  • Search search internally what knowledge and skills might be helpful to solve it
  • Attempt to apply relevant knowledge and skills to the task
  • Finally conntect multiple skills and knowledge

• Given a task and a set of reasoning module descriptions representing high-level problem-solving heuristics ("Use critical thinking", "Let's think step by step"), Stage 1 aims to undercover the intrinsic reasoning structure via meta-resoning

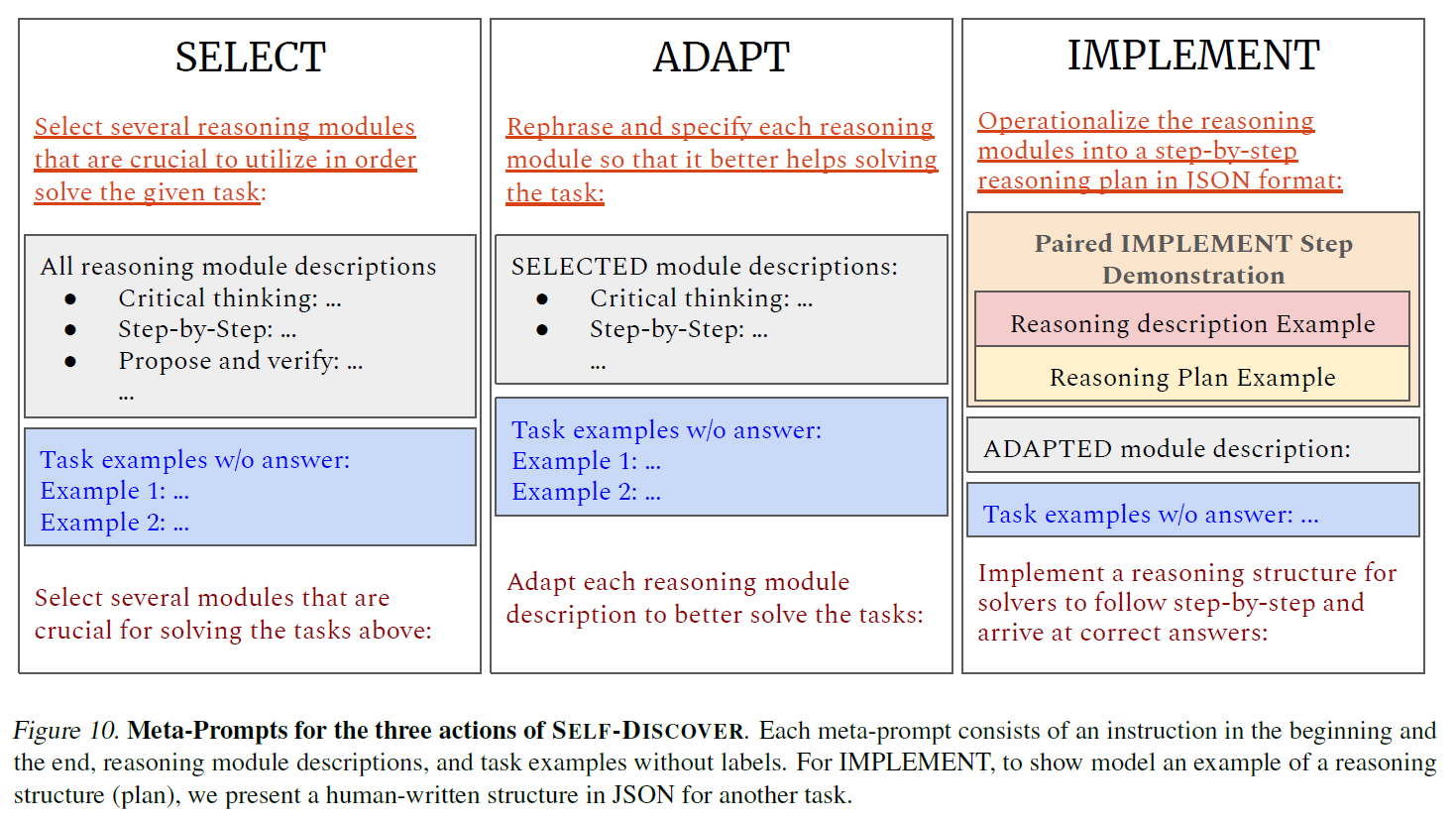
  • Three meta-prompt to guide LLM to select, adapt, implement an actionable reasoning structure without labels or training

  • Formatted the structure in key-value pairs like JSON due to interpretability and performance

  • 

  • this operates on Task-Level so this stage is only needed once for each task

  • Use discovered reasoning structure to solve every instance of task

    • Follow the step-by-step reasoning plan in JSON to correctly solve the task. Fill in the values following the keys by reasoning specifically about the task given. Do not simply rephrase the keys

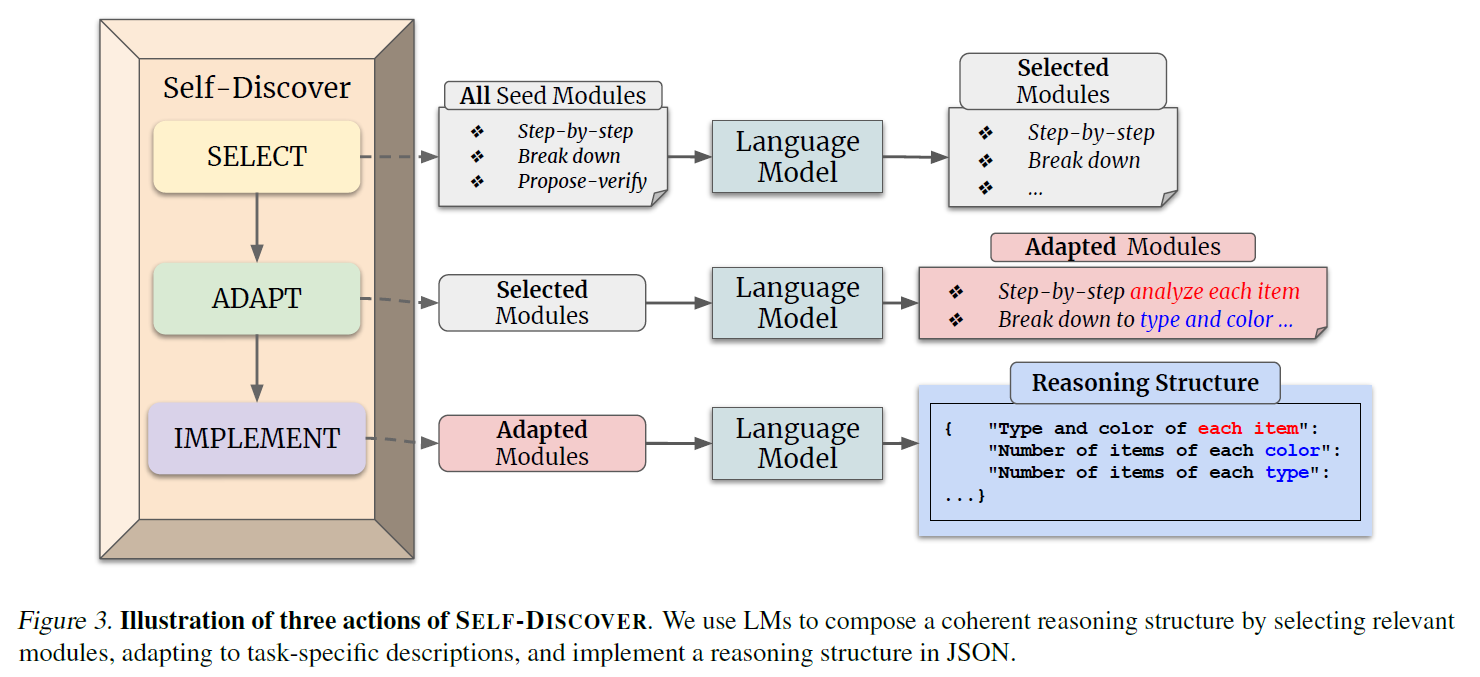
2.1 Stage 1 : Self-Discover Task-Specific Structures

SELECT

• Not every reasoning module is helpful

• Guide LLM to select module based on task example

• given raw set of reasoning module $D$ and a few task examples without labels $t_i \in T$, Self-Discover selects a subset of reasoning modules $D_S$ by a model $\mathcal{M}$ and a meta-prompt $p_S$

  • $D_S = \mathcal{M}(p_S \ || \ D \ || \ t_i)$

ADAPT

• Each reasoning module provide general description of how to solve problems

• Self-Discover aims to tailor each module

  • "break the problem into subproblems" $\rightarrow$ "calculate each arithmetic operation in order" for arithmetic problems

• given $D_S$ and meta-prompt $p_A$, the model generates the adapted reasoning module descriptions $D_A$

  • $D_A = \mathcal{M}(p_A \ || \ D_S \ || \ t_i)$

IMPLEMENT

• Given adapted reasoning module descriptions $D_A$, it uses the reasoning modules into an implemented reasoning structure $D_I$ with specified instruction on what to generate for each step

• Provide a human-written reasoning structure $S_{\text{human}}$ on another task in addition to meta prompt to better convert the natural language descriptions into a reasoning structure

  • $D_I = \mathcal{M}(p_A \ || \ S_{\text{human}} \ || \ D_A \ || \ t_i)$

2.2 Stage 2 : Tackle Tasks Using Discovered Structures

• After those stages, use $D_I$ which is uniquely adapted for the task to solve $T$
• $A = \mathcal{M}(D_S \ || \ t), \quad \forall t \in T$

3. Experiment Setup

Tasks

• Used diverse reasoning benchmarks challenging for LLMs

  • Big Bench Hard (23 challengine tasks from Big-Bench)

    • Algorithmic and Multi-Step Arithmetic Reasoning
    • NLU
    • Use of Wold Knowledge
    • Multilingual Knowledge and Reasoning

  • Thinking for Doing (T4D)

    • models must leverage mental state reasoning to determine actions to perform (GPT-4 + CoT reached only 50%)

  • MATH test set (200 samples)

Models

• GPT-4 (gpt-4-turbo)
• GPT-3.5 (chatGPT, gpt-3.5-turbo)
• instruction tuned PaLM2-L
• Llama2-70B

Baselines

• Zero-shot prompting

  • Direct Prompting
  • CoT
  • Plan-and-Solve (firstly generate a plan and solve problem)

• use the raw seed reasoning modules passed to Self-Discover

  • CoT-Self-Consistency (sample multiple outputs with CoT and aggregate answer)
  • Majority voting of each RM
  • Best of each RM (uses highest accuracy from each RM

• To test universality of reasoning structure, comparing with Prompt-optimization that requires a training set (OPRO)

  • showing when applyting structures or prompt that optimized from one model, the reasoning structure can retain more performance

4. Results

4.1 Does Self-Discover Improve LLM Reasoning?

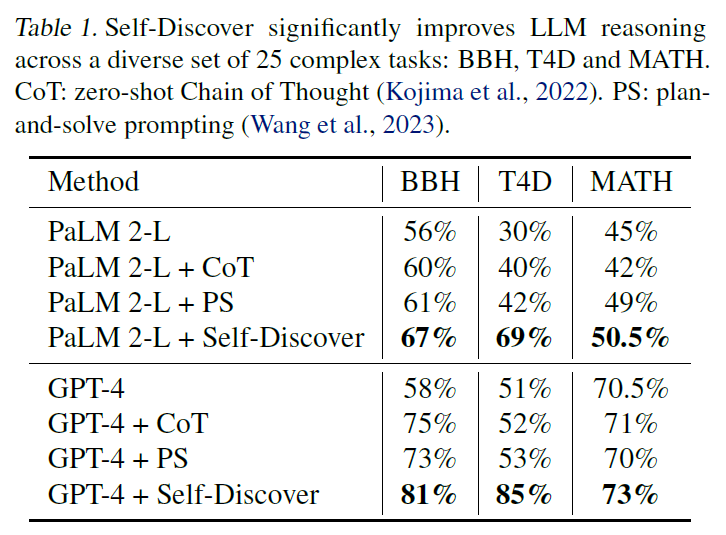
• For MATH, upon error analysis, the reasoning structures generated by PaLM 2-L from Self-Discover are correct 87.5% of the time (Human can follow the structures to solve the tasks perfectly)

4.2 Which Types of Problems Do Self-Discover Help the Most?

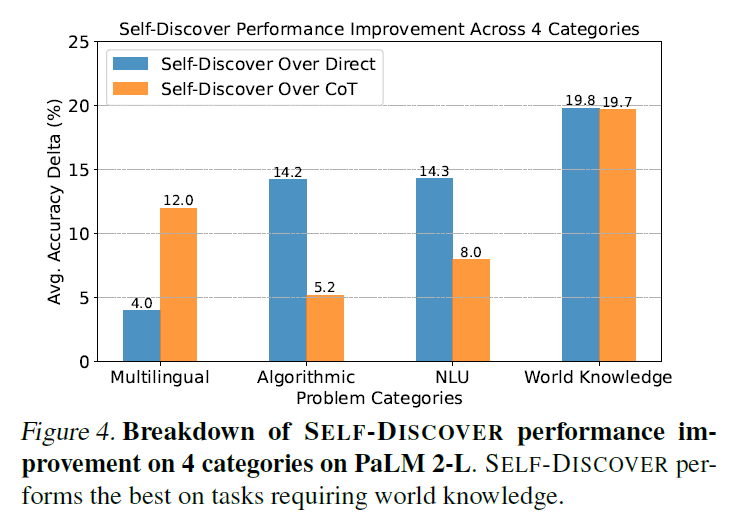
• Self Discover improved the performance of World Knowledge task the most (sports understanding, movie recommendation, ruin names)

• Using CoT misses the key knowledge

• Algorithmic category's gain is moderate which is consistent with MATH result from 4.1

4.3 How Efficient is Self-Discover?

• Self-Discover achieves the best performance while requiring 10-40x fewer inference call compared to Self-Consistency and Majority voting

4.4 Qualitative Examples

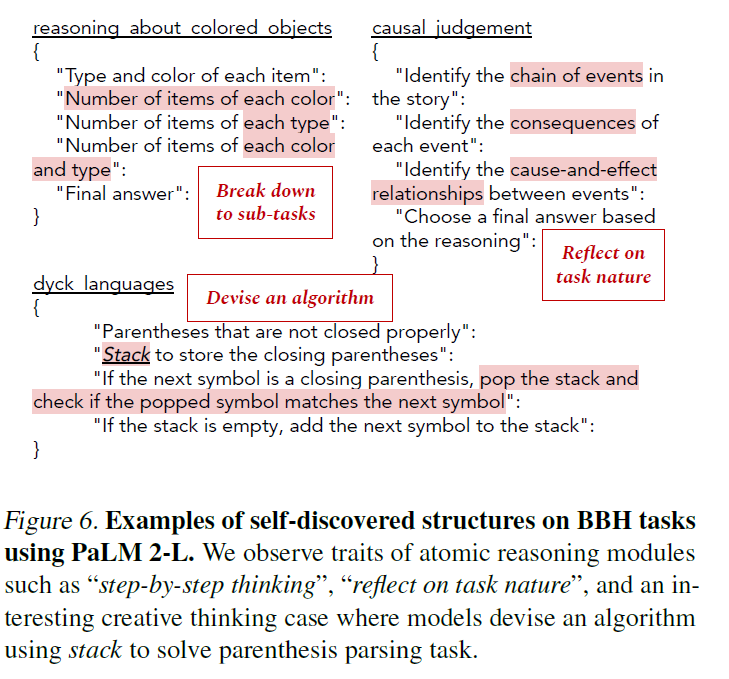
5. Deep Diving Into Self-Discovered Reasoning Structures

• All actions of Self-Discover needed

5.1 Importance of Self-Discover Actions

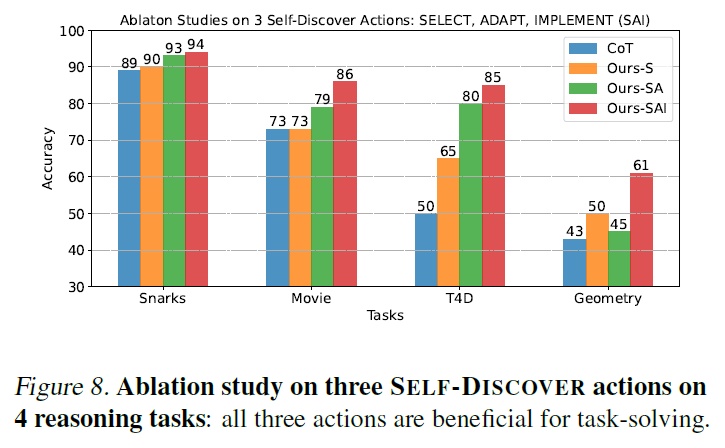
• S for only SELECT / SA for SELECT and ADAPT
• Adding each step, the model's zero-shot reasoning capability improved $\rightarrow$ All three step is beneficial

5.2 Towards Universality of Discovered Reasoning Structure

Applying PaLM 2-L Discovered Structures to GPT-4

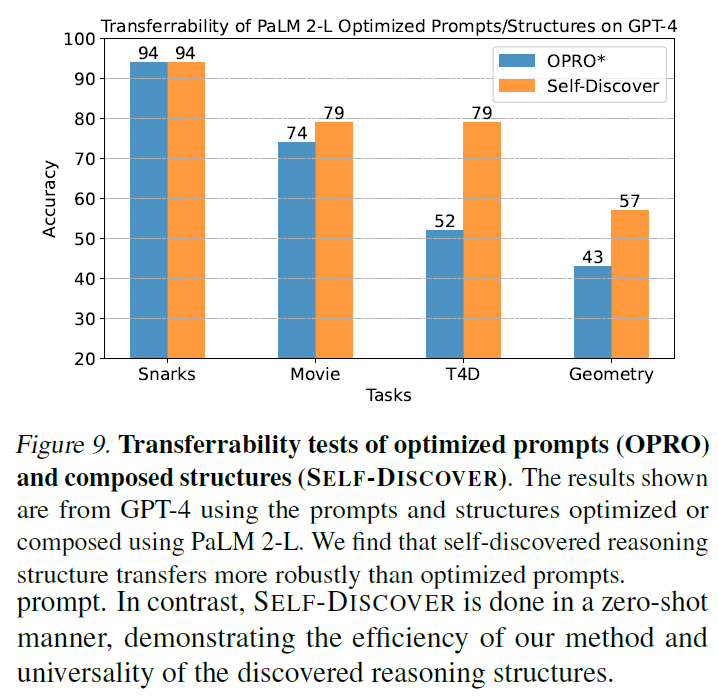
Applying GPT-4 Discovered Structures to Llama2 and ChatGPT

• Llama2 + Self-Discover (52%) > CoT (42%) on zero-shot disambiguation QA
• GPT-3.5 (56%) > CoT (51%) on geometry with 3-shot

6. Related Work

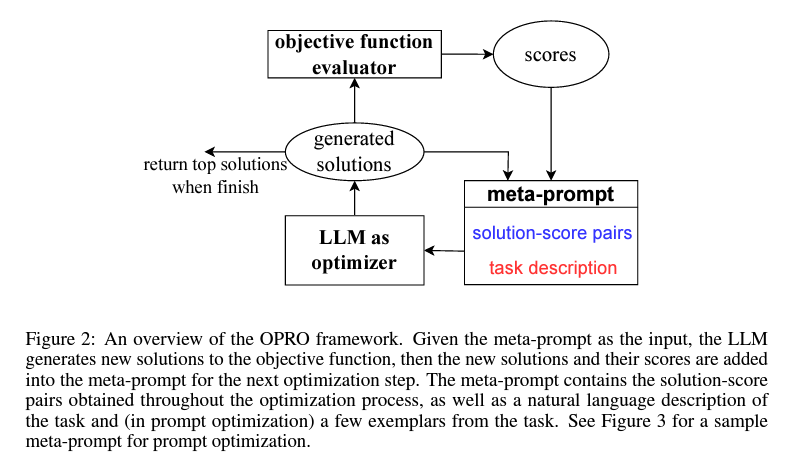
OPRO Framework (LLMs as optimizers, Yang et al., 2023)

7. Conclusion

• Self-Discover a reasoning structure for any task
• Drastic improvements from challenging task
• the composed reasoning structure is transferable

8. Comment

문제를 푸는 구조까지 LLM의 판단에 맡기는 파이프라인. 대형 모델에서 효과를 봤다는 점이 인상적인듯.