Abstract

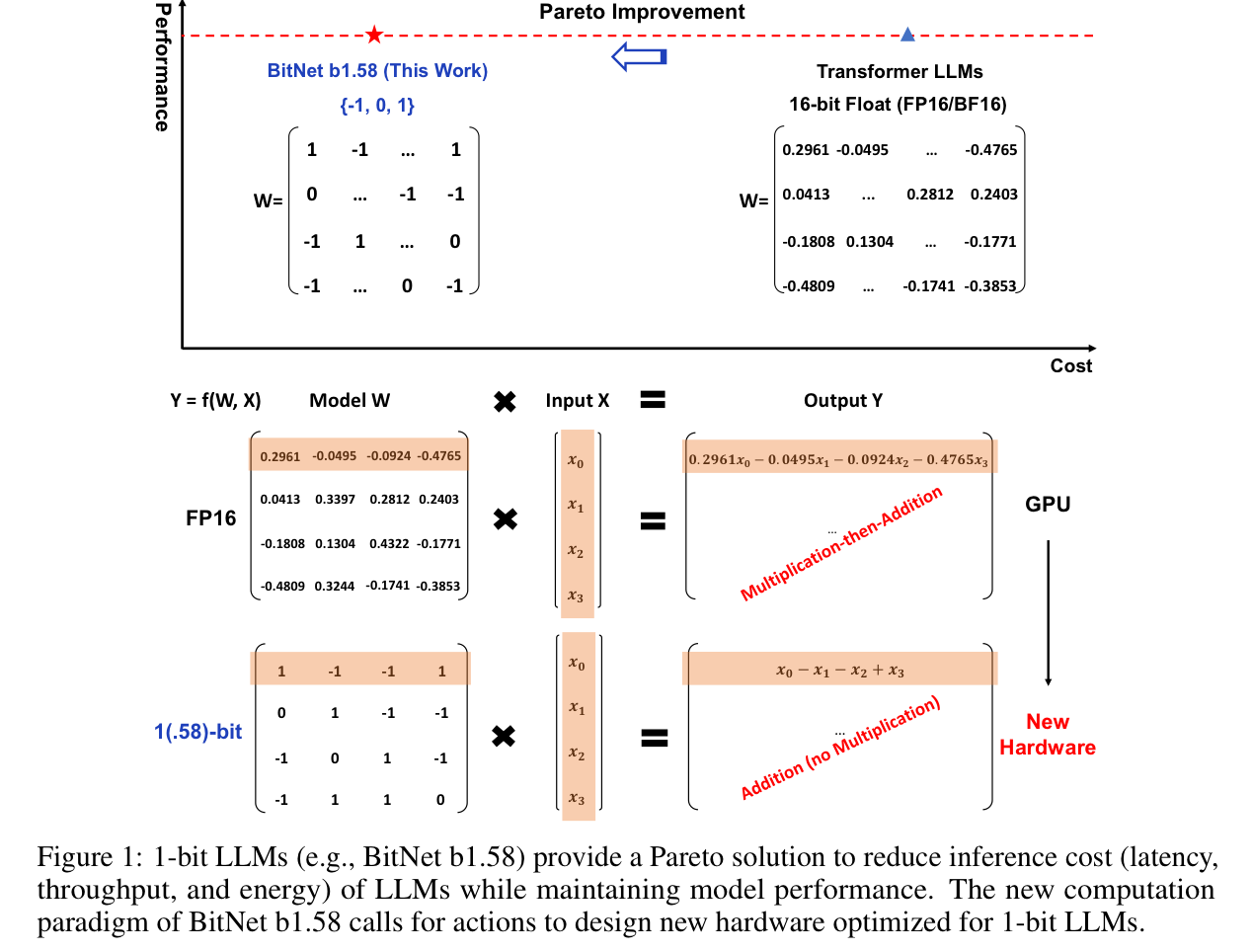
• BitNet paved the way for a new era of 1-bit LLMs

• BitNet b.58 has every parameter as a tenary {-1, 0, 1}

  • matches a full-precision Transformer with the same model size
  • significantly more cost-effective

• defines new scalinglaw and recipe for training

1. The era of 1-bit LLMs

• The recent LLMs' size is increasing

  • remarkable performance on LLM tasks

  • high energy comsumption

    • challenges for deployment
    • environmental and economic impact

• Post-training quantization to create low-bit models for inferenct

  • reduces weights and activations
  • 16 bits to lower bits (4-bits)
  • sub-optimal

• BitNet presents a direction for reducing the cost of LLMs while their performance

• the major computation cost comes from the floating-point addition and multiplication

  • BitNet has only integer addition

• transferring model parameters from DRAM to the memory of an on-chip accelerator (SRAM) can be expensive during inference

  • enlarging SRAM to improve throughput $\rightarrow$ significantly higher costs than DRAM
  • 1-bit LLMs have a much lower memory footprint from both a capacity and bandwidth standpoint

• BitNet b1.58

  • added 0 to original BitNet
  • retains all the benefits of the original BitNet
  • included new computation paradigm (no multiplication for matmul)
  • same energy consumption as the original BitNet
  • stronger modeling capability $\rightarrow$ explicit support for reature filtering by inclusion of 0
  • it can match full precision baselines in terms of PPL and end-task starting from 3B

2. BitNet b1.58

Recap: BitLinear

1. Binarize weights to +1 or -1 with signum function

• Centralize to be zero-mean to increase the capacity witnin a limited numerical range
• Use scaling factor $\beta$ after binarization to reduce l2 error between real-valued and the binarized.

2. Quantize activations to $b$-bit precision with absmax

• $Q_b = 2^{b-1}$

• $\epsilon$ is a small floating-point number that prevents overflow in clipping

  $\tilde{x} = \text{Quant}(x) = \text{Clip} \left( x \times {Q_b \over \gamma}, -Q_b + \epsilon , Q_b - \epsilon \right)$
  $\gamma = ||x||_{\infin}$

• For activations before non-linear functions (ReLU) $\rightarrow$ scale into $[0, Q_b]$ by subtracting the minimum of the inputs

  $\tilde{x} = \text{Quant}(x) = \text{Clip} \left( (x-\eta) \times {Q_b \over \gamma}, \epsilon, Q_b - \epsilon\right)$
  $\eta = \min _{ij} x_{ij}$

• quantize with 8-bit

• Training $\rightarrow$ quantize per tensor / Inference $\rightarrow$ quantize per token

3. Matrix Multiplication
   $y = \tilde{W} \tilde{x}$

The variance of the output $y$ under following assumption

• the elements in $W$ and $x$ are mutually independent and share same distribution
• $W$ and $x$ are independent of each other

In full-precision, $\text{Var}(y) = 1$ with standard initialization method $\rightarrow$ training stability. To preserve this stability, use LayerNorm function.

• $\text{Var}(y) \approx E[\text{LN}(\tilde{x})^2] = 1 \quad \quad \quad (\text{SubLN})$

Then, the final representation of BitLinear is:

${\beta\gamma \over Q_b}$ means Dequantization to restore original precision

4. Model Parallelism with Group quantization and Normalization

• Calculate all parameters $\alpha, \beta, \gamma, \eta$ with each group (device)
• If the Number of group is $G$, then the parameter becomes
  $\alpha_g = {G \over nm} \sum _{ij} W_{ij} ^{(g)}, \quad \quad \beta_g = {G \over nm} ||W^{(g)}||_1, \\ \gamma_g = ||x^{(g)}||_{\infin}, \quad \quad \eta_g = \min _{ij} x_{ij} ^{(g)}$
• LayerNorm should also be applied with similar way

BitNet B1.58

• based on the BitLinear

• trained from scratch, 1.58-bit weights and 8-bit activations

• adopted absmean quantization

  • scales the weight by its average absolute value

  • round each value to the nearest integer among {-1, 0, 1}

    $\begin{aligned} \tilde{W} &= \text{RoundClip}({W \over \gamma + \epsilon}, -1, 1) \\ \text{RoundClip}(x, a, b) &= \max(a, \min(b, \text{round}(x))) \\ \gamma &= {1 \over mn} \sum_{ij} |W_{ij}| \end{aligned}$

  • don't scale the activations before the non-linear functions to the range $[0, Q_b]$

  • scale all activations to $[-Q_b, Q_b]$ per token to get rid of the zero-point quantization

    • more convenient and simple for both implementation and system-level optimization

LLaMA-alike components

• used LLaMA alike components
  • RMSNorm
  • SwiGLU
  • rotary embedding
  • removed all biases
• it can be integrated into the popular open-source software

3. Results

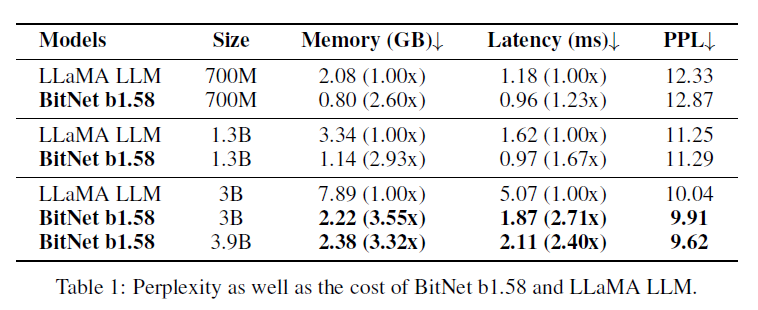
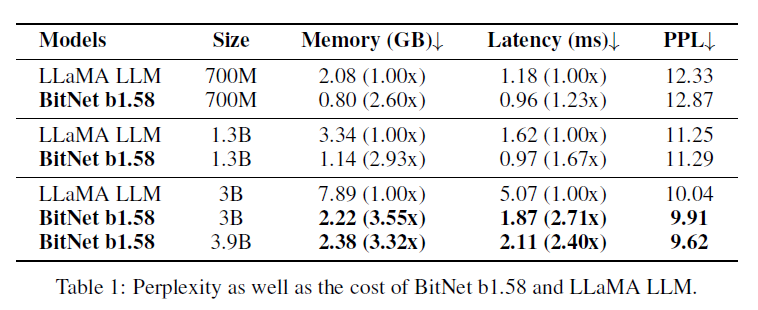
• BitNet b1.58 vs FP16 LLaMA

• pretrained on RedPajama for 100B tokens

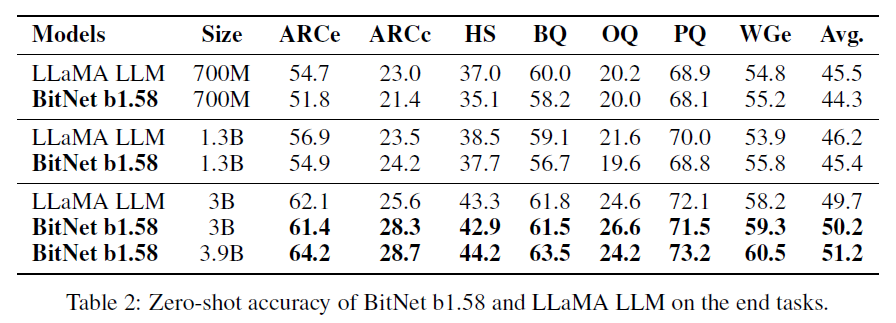
• zero-shot performance

  • ARC-Easy
  • ARC-Challenge
  • Hellaswag
  • Winogrande
  • PIQA
  • OpenbookQA
  • BoolQ

• validation PPL

  • WikiText2
  • C4

• runtime GPU memory and latency

  • FasterTransformer codebase
  • 2-bit kernel from Ladder in BitNet
  • the time per output token

• BitNet starts to match FP LLaMA at 3B size

• BitNet b1.58 3.9B outperforms FP LLaMA 3B

• the performance gap between BitNet and LLaMA narrows as the model size increases

• in terms of zero-shot performane, BitNet starts to match LLaMA at 3B size

• BitNet b1.58 3.9B outperforms LLaMA $\rightarrow$ BitNet b1.58 is a Pareto improvement over the SOTA LLMs

Memory and Latency

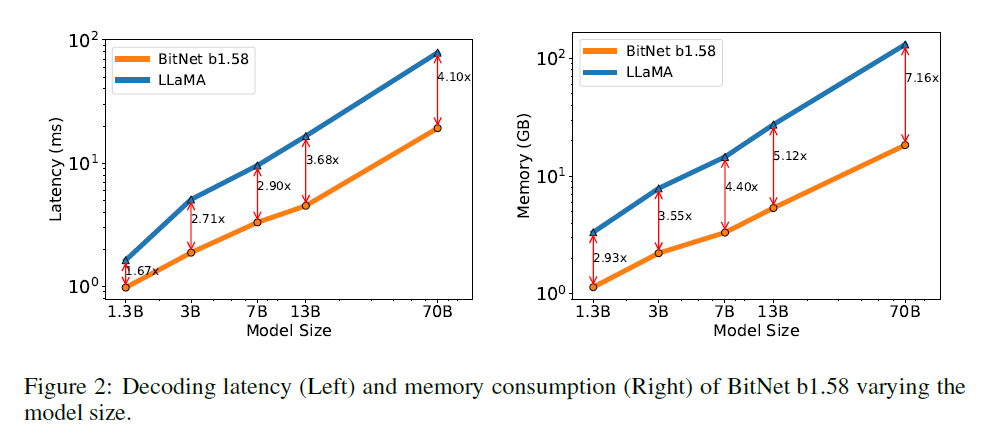
• the speed-up increases as the model size scales
  • the proportion of nn.Linear increases as the model size grows
• for the memory, the trend follows that of the latency
  • as the embedding remains full precision and its proportion gets smaller
• Both were measured with a 2-bit kernel
  • there is still room for optimization

Energy

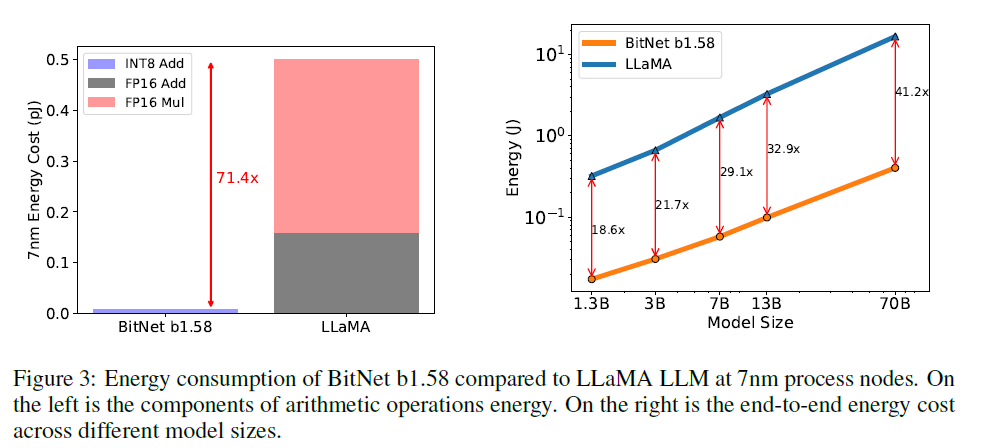
• for LLaMA model, the majority of matmul is FP16 multiplication while for BitNet, it is INT8 addition

• BitNet is more efficient when model is large

  • as the percentage of nn.Linear grows with the model size

Throughput

• compared on two A100 80G cards

• BitNet b1.58 and LLaMA 70B

• maximum batch size for the GPU memory

BitNet b1.58 is enabling a new scaling law w.r.t. model performance and inference

• in terms of latency, memory usage and energy consumption,
  • BitNet 13B > FP16 3B
  • BitNet 30B > FP16 7B
  • BitNet 70B > FP16 13B

Training with 2T tokens

• to test scalability in terms of token

• same recipe with StableLM 3B

• evaluated on

  • Winogrande
  • PIQA
  • SciQ
  • LAMBADA
  • ARC-easy

• It has strong generalization capabilities

4. Discussion and Future Work

1-bit MoE LLMs

• MoE has high memory comsumption and inter-chip communication overhead

• BitNet b1.58 can handle them

  • reduced memory footprint reduces the number of devices required to deploy MoE models
  • there would be no overhead if the entire models could be placed on a single chip

Native Support of Long Sequence in LLMs

• the issue in handling long sequence is the memory consumption introduced by the KV caches

• BitNet b1.58 reduces activations from 16-bits to 8-bits

  • doubling the sequence length
  • if reducing to lower than 4 bits is possible, the length would be longer

LLMs on Edge and Mobile

• for Edge and Mobile device, BitNet b1.58 can resolve the issue of memory and computational power

• BitNet is more friendly to CPU devices

New Hardware for 1-bit LLMs

• Groq demonstrated promising results and great potential for specific LLMs (LPU)
• expect new hardware for 1-bit LLM

5. Comment

두 번 날려먹고 다시 쓰는 코멘트. 1bit 모델의 가능성을 보여주었다면, 조금 더 다듬어진 듯한 논문. 온디바이스나 3진법 반도체가 떠오르게 하는 글이었음. 왜 처음에 0을 넣지 않았는지, 그리고 양자화 범위의 구분이 어떤 효과를 주는지 설명해주었다면 좋았을듯