1. Introduction

• LLM Acceleration

  • sparsity
  • quantization
  • head pruning

• Reducing the number of layers for each token by exiting early during inference

• Speculative decoding

  • main model + draft model

  • larger memory footprint and complexity

  • faster inference

    $\rightarrow$ Self-Speculative Decoding

• contribution

  • training recipe that combines layer dropout and early exit loss

  • the recipe more robust to exiting at earlier layers of the model, essentially creating different sized sub-models within the same model

  • self-speculative decoding solution that decodes with earlier layers and verifies and corrects with later layers

    

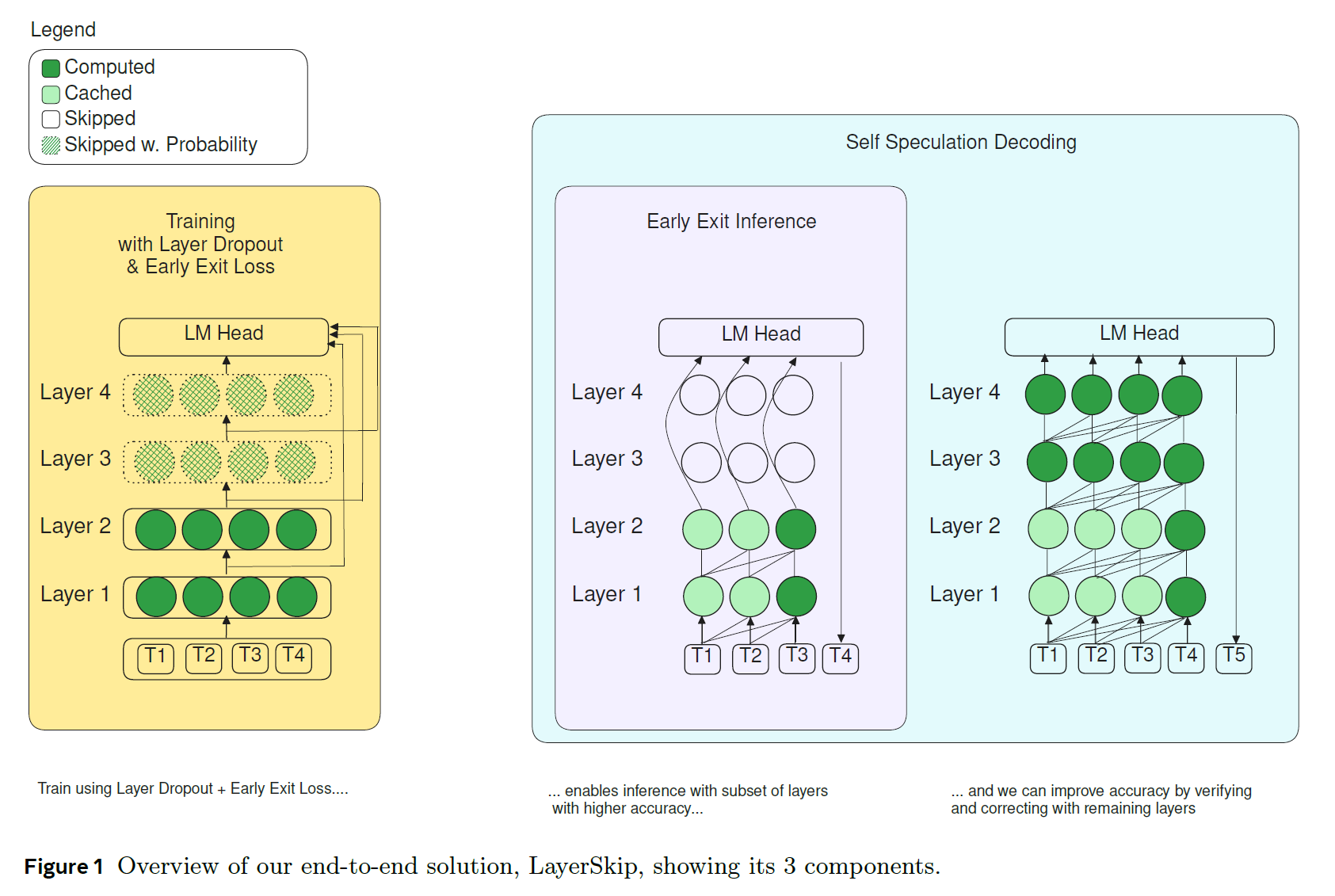
2. Motivation

2.1. Exiting Earlier in LLMs

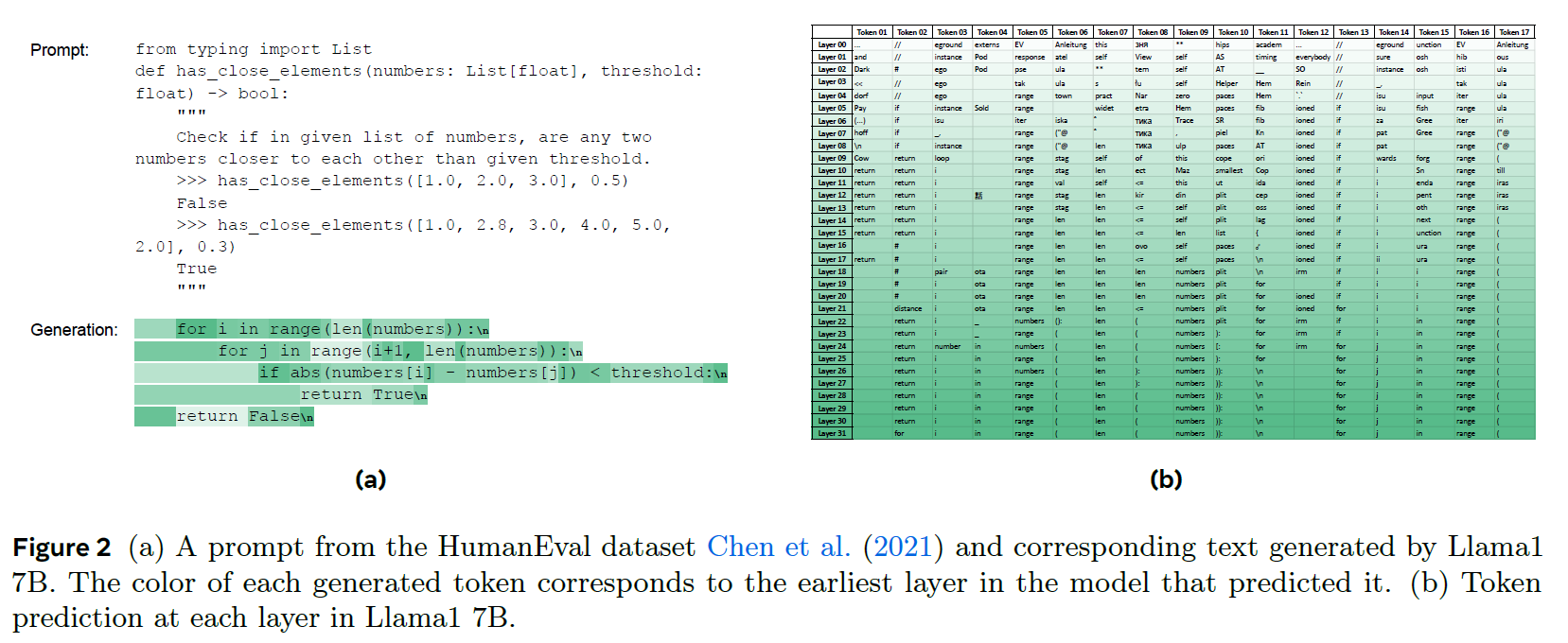
• Fig 2a -> Llama1 7B + HumanEval coding dataset

• projected each layer's output embeddings on the LM head + softmax $\rightarrow$ got the index of the output element (Unembedding)

  • token predictions in earlier layers appear to be irrelevant

  • in later layers, token predictions converge to the final prediction

  • most of the time, the final token predition is predicted fewer layers before the end

  • intermediate layers are sometimes hesitant and change their mind

  • a token requires 23.45 layers out of the model's 32 layers

    $\rightarrow$ need to make the model to use fewer layers

    $\rightarrow$ make the model not to hesitate and change their mind

• skipping layers during training (dropout)

  • higher rate for later layers and lower rates for earlier layers

• unembedding

  • typically LLMs are trained to unembed at the last transformer layer

  • need to adds a loss function during training to make the LM heads understand embeddings of earlier layer

  • shared LM head to early exit

    

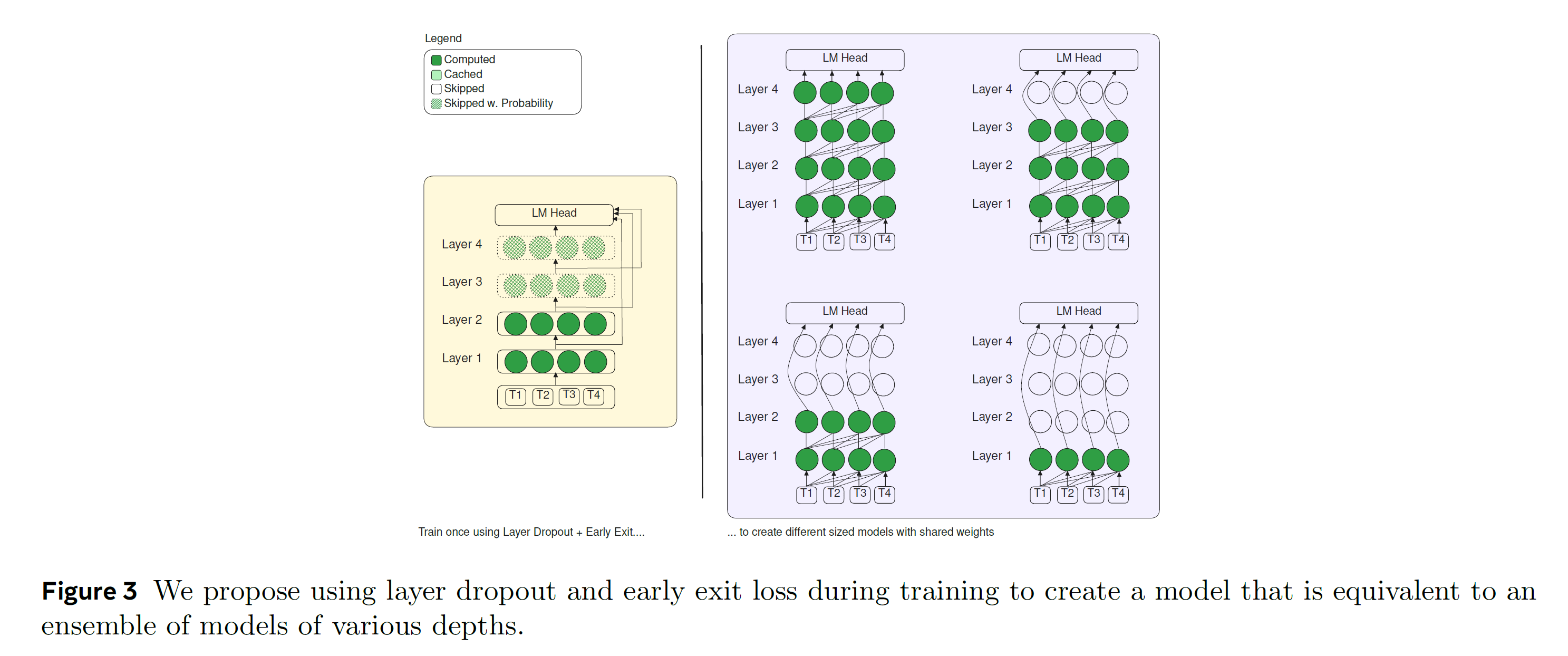
  • make the LM head as ensemble of different depth models with same weight

2.2. Correcting if we exit too early

• exiting early can reduce the accuracy
  • needs a way to verify if an early prediction is accurate and correct it by using remaining layers
  • Self-speculative decoding

3. Related Work

Dropout

• unstructured dropout (original)

• large models (Llama, GPT3, PaLM) don't use it at large corpus

• enable the training to learn across an ensemble of many models

• multiplicative noise

Layer Dropout (stochastic depth)

• stochastically skipping layers

• LayerDrop in LMs $\rightarrow$ robustness

• layer dropout for training decoder-only models or scaling LMs has not beed explored

Early Exit

• branch modules at different exit points in a deep learning network + additional loss

• in LMs, early exit in encoder-only models was explored

• dedicated LM head for each decoder layer

• SkipDecode

• additional FC layer

Speculative Decoding

• auto-regressive decoding is slow while measuring the likelihood of a group of generated tokens in parallel is faster

• draft model (fast, less accurate) to generate tokens and verify and correct with main (slow, more accurate) model

4. Proposed solution

4.1. Training using Layer Dropout & Early Exit Loss

• Notation
  • model $X$
  • output $Y$
  • token embeddings $x_0$
  • number of layers $L$
  • $x_{l+1} = x_l + f_l (x_l)$
  • final LM head maps the embedding outputs to logits $e_L = g(x_L)$
  • BCE loss = $J_{\text{BCE}}(e_L, Y)$

4.1.1. Layer Dropout

• layer dropout at layer $l$ and iteration $t$
  • $x_{l+1, t} = x_{l, t} + M(p_{l, t})f_l(x_{l, t})$
  • where $M$ is bernoulli function that returns 0 with probability $p$
  • apply dropout on each sample separately within a batch
  • remove dropped sample and apply transformer operation $f_l$ on the remaining samples
  • same random seed for GPUs
• Dropout rate $p_{l, t} = S(t)D(l)p_{max}$
  • $p_{max}$ : hyperparameter
  • $D(l)$ : per-layer scaling function
  • $D(l) = e^{{l \ln 2 \over L-1}} - 1$ was the best (growing exponentially)
  • $S(t)$ : per-time step scaling function
  • for pre-trained model and doing fine-tuning or continuous training, $S(t) = 1$ was the best
  • for pretraining from scratch, $S(t) = e^{{t \ln 2 \over T-1}} - 1$ was the best

4.1.2. Early Exit Loss

• LM head $g$ should be capable of unembedding outputs of different layers

• During training, supervise the model directly to connect the early exit layers to the LM head

  • $J(X, Y, t) = \displaystyle \sum_{l=0}^{l = L-1} \tilde{e}(t, l) J_{\text{BCE}}(g(x_{l+1}), Y)$
  • $\tilde{e}(l) = {C(t,l)e(l) \over \sum_{i=0}^{i=L-1} C(t,i)e(i)}$, normalized per-layer loss scale
  • $C(t, l)$ : Binary curriculum function that determines if we enable early exit of layer $l$ at iteration $t$
  • $e(l) = \begin{cases} e_{scale} \sum_{i=0}^{i=l} i \quad &\text{if } 0 \le l < L-1 \\ L-1 + e_{scale} \sum_{i=0}^{i=L-2}i &\text{if } l = L-1 \end{cases}$
  • the scale increases across layers
  • the scale at one layer is proportional to the sum of the scales of all previous layers
  • penalize later layers with quadratically higher weight (predicting in later layers is easier)
  • $0 \ \le e_{scale} \ \le 1$ is a hyperparameter

Early Exit Loss Curriculum

• adding early exit loss of all layers at all iteration slows down the training and reduces the accuracy

• use $C(t, l)$

  • rotational early exit curriculum $C_{\text{rot}, R}$

    • enable early exit at every $R$ layers
    • only $\lceil L/R \rceil$ unembedding operations are applied

  • gradual early exit curriculum $C_{\text{grad}}$

    • gradually enable early exit loss from layers $L-1$ to 0, one layer at a time every $T/2L$ iterations

Hyperparameter Summary

• Layer Dropout
  • $p_{max}$ : max dropout rate of last layer of the model
  • $S(t)$: layer dropout curriculum
• Early Exit Loss
  • $e_{scale}$: scalar scale of loss of earlier layers
  • $C(t,l)$: early exit loss curriculum

4.2. Inference using Early Exit

• run the first $E$ transformer layers and skip to the model's LM head

• the final output is $g(x_E)$

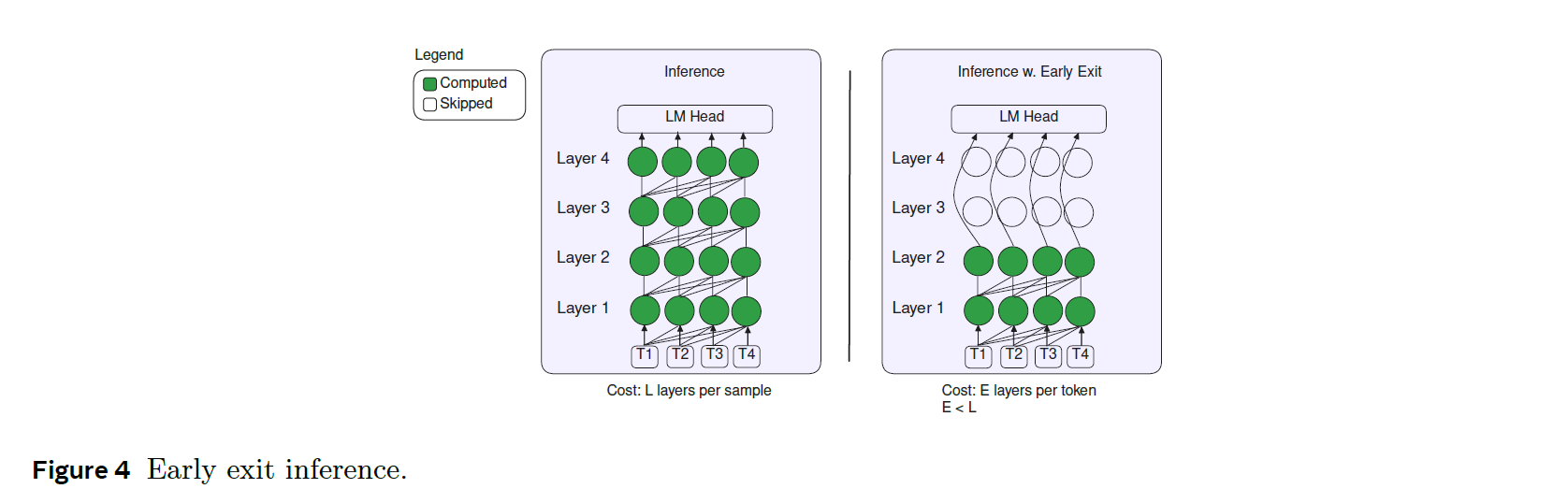
4.3. Inference using Self-Speculative Decoding

• Self-speculative decoding

  • use single model and latency of traditional speculative decoding

  • Self Drafting and Self-Verification

    

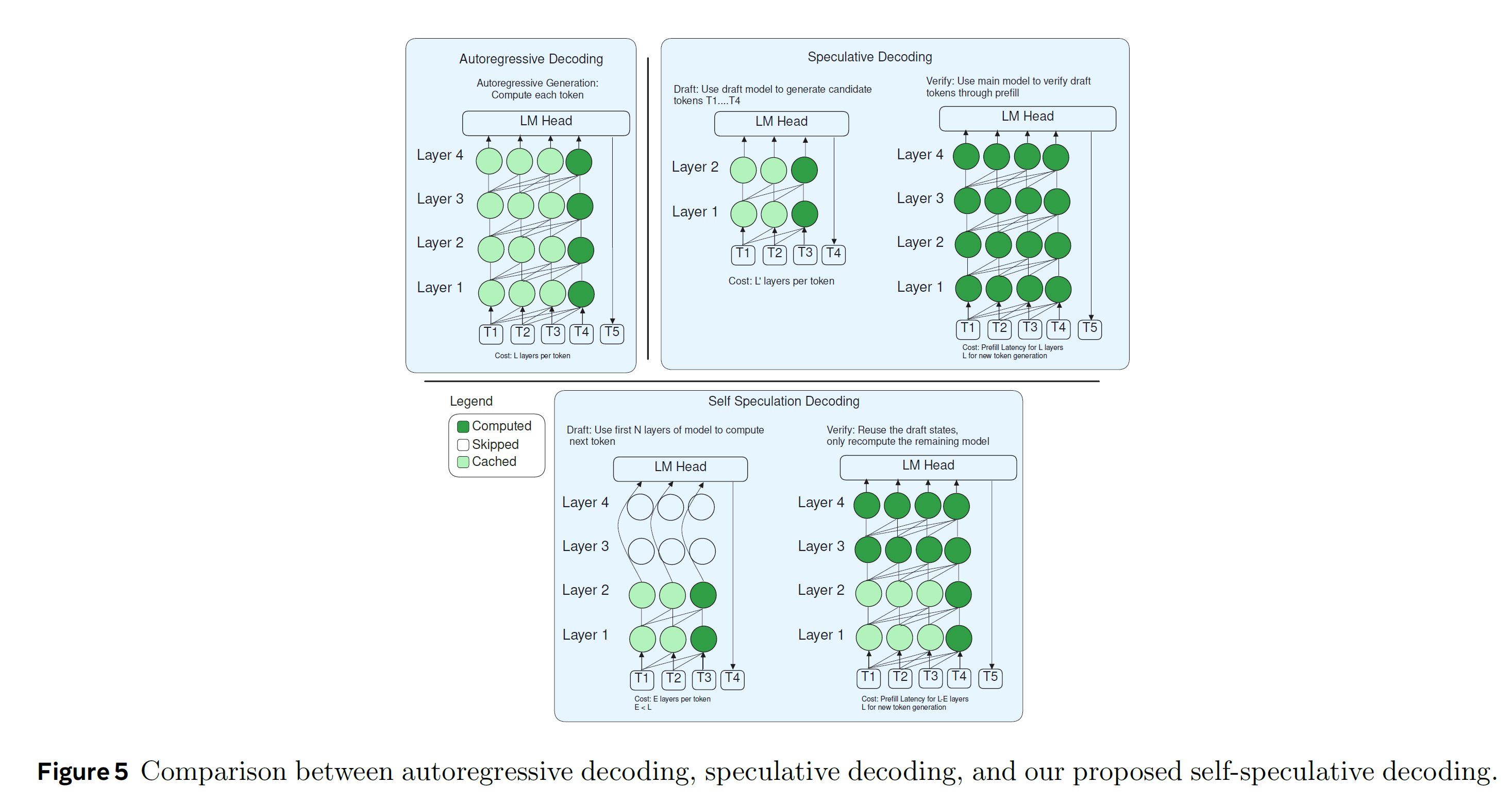
  • Self Drafting: using the early exit to draft tokens

  • Self Verification: using the remaining layers to validate the prediction

  • Cache Reuse : unifies the KV cache and storing the exit query

4.3.1. Self-Drafting

• compute the first $d$ draft tokens through early exit
  • leverage a subset of the LLM and conduct auto-regressive inference exiting at layer $E$
  • train the model once to get an ensemble of different candidate draft models at each layer depth

4.3.2. Self-Verification

• leverages the full LLM to predict the next token for each draft token in a single forward pass

• find the point where the draft tokens and verified tokens agree

• All the draft tokens up till the disagreement point are added to the output along with the next verified token and continues from the draft

• only computes $L-E$ layers

4.3.3. Reusing the Cache

• avoid recomputing prior KV pairs in each layer
  
• Single KV Cache
  • first $E$ layers are shared in two stages
• Exit Query Cache
  • saves the query vector of exit layer $E-1$ for verification to directly continue from layer $E$
  • save only the query for the exit layer

5. Experiments

• Continual Pretraining

  • continue training with 52B tokens

  • text + code

  • Llama2 7B (32 layers)

    • $p_{max} = 0.1$
    • $e_{scale} = 0.2$
    • $C_{\text{rot}, R=8}$

  • Llama2 13B (40 layers)

    • $p_{max} = 0.1$
    • $e_{scale} = 0.1$
    • $C_{\text{rot}, R=39}$
• Pretraining from scratch

  • 26B tokens

  • text + code

  • Llama2 1.5B (24 layers)

    • $p_{max} = 0.1$
    • $e_{scale} = 0.2$
    • $C_{\text{rot}, R=23}$

  • Llama2 7B (32 layers)

    • $p_{max} = 0.2$
    • $e_{scale} = 0.2$
    • $C_{\text{rot}, R=31}$

  • higher LR when dropout $\ge$ 0.0

• Fine-tuning on Code

  • 5.2B tokens

  • Llama1 7B

    • $p_{max} = 0.1$
    • $e_{scale} = 1.0$
    • $C_{\text{rot}, R=16}$
• Fine-tuning on Task-Specific Dataset

  • TOPv2 dataset

  • Llama 1.5B (24 layers)

    • $p_{max} = 0.2$
    • $e_{scale} = 1.0$
    • $C_{\text{grad}}$
• tried LD, EE, LD+EE

6. Results

6.1. Early Exit Inference Results

Continual Pretraining

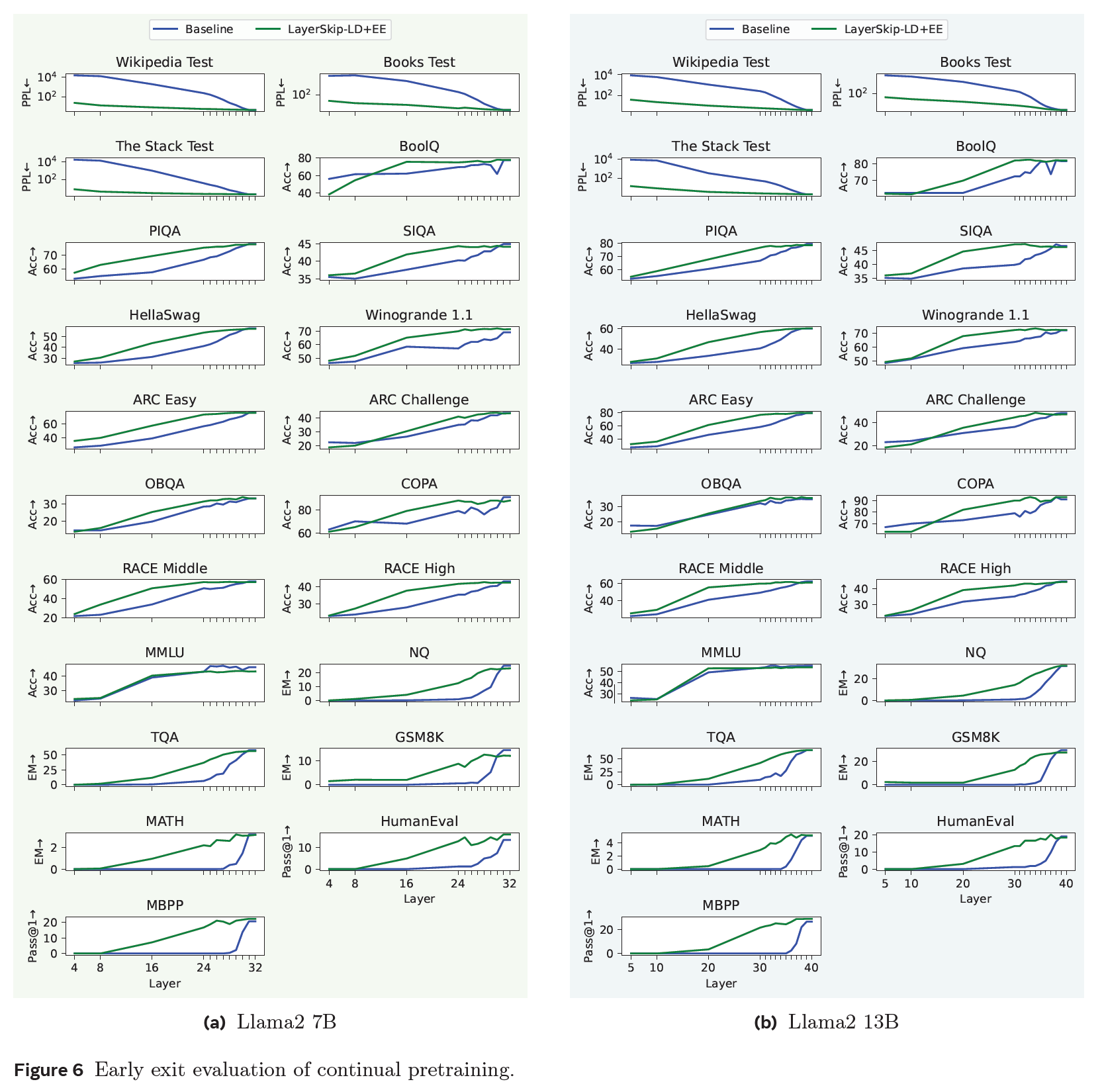
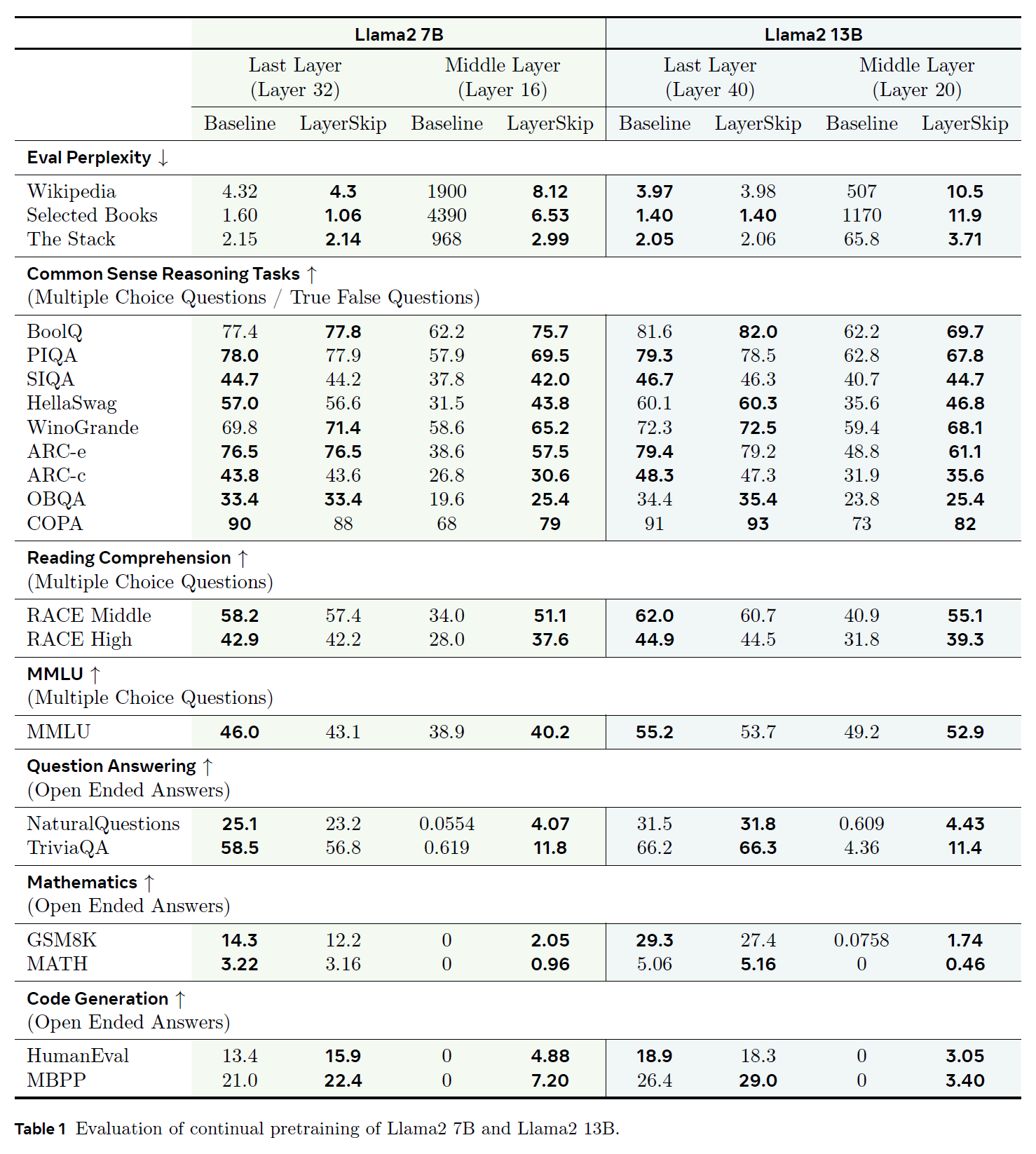
• LayerSkip is better than the baseline

• for the last layer accuracy, LayerSkip has minimal drop in accuracy

• some classification tasks (multiple choice, TF) $\rightarrow$ maintain relatively decent accuracy on earlier layers

• generation task $\rightarrow$ drop drastically

• classification is evaluated on one token while generation is evaluated on many tokens

• in MMLU, Llama2 13B baseline dropped from 55.2 to 49.2

• NaturalQuestions $\rightarrow$ LayerSkip's accuracy is higher at middle layer

Pretraining from Scratch

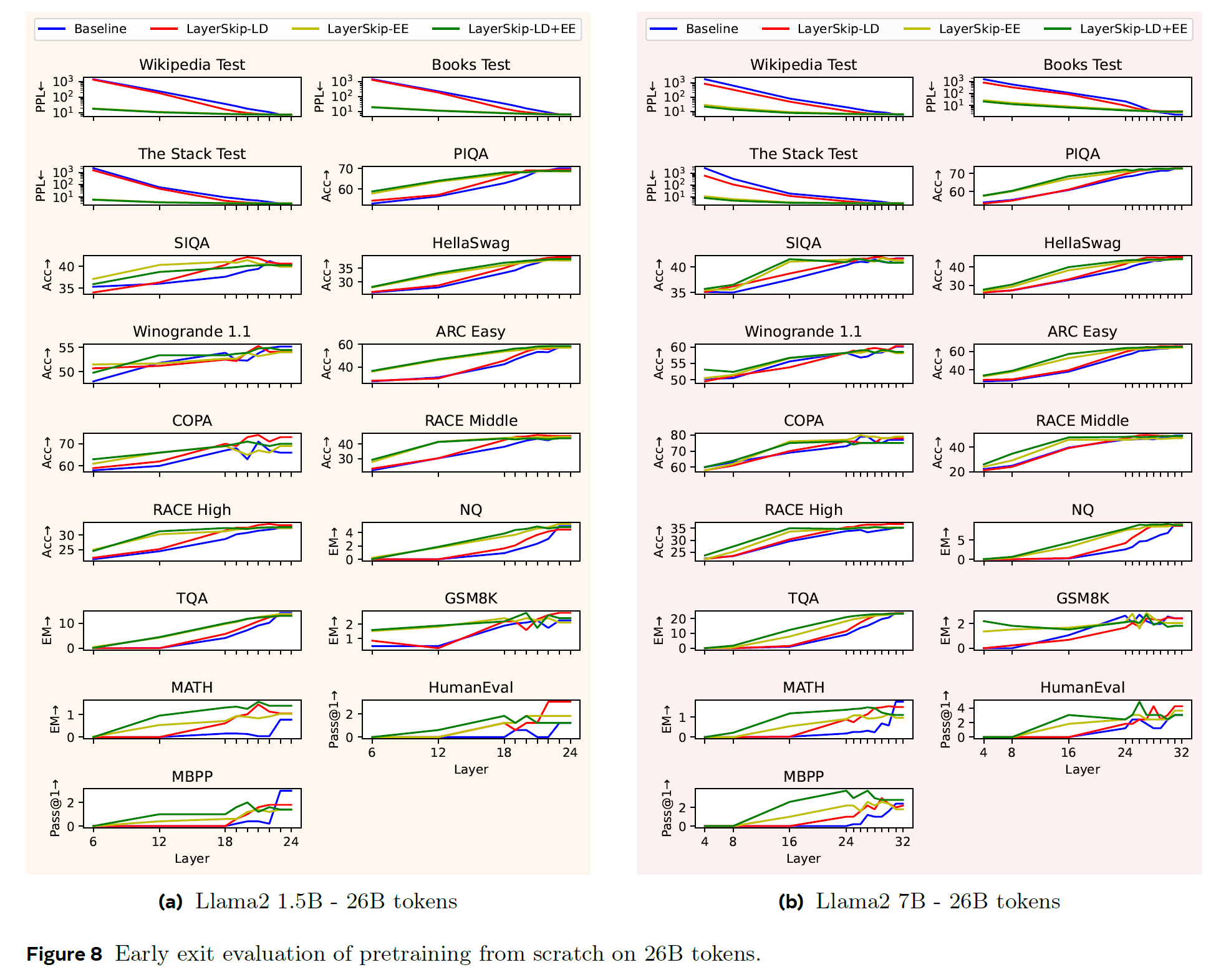
• on the last layer in some downstream tasks, a slight drop in accuracy is seen
  • small tokens $\rightarrow$ some tasks were close to random guess

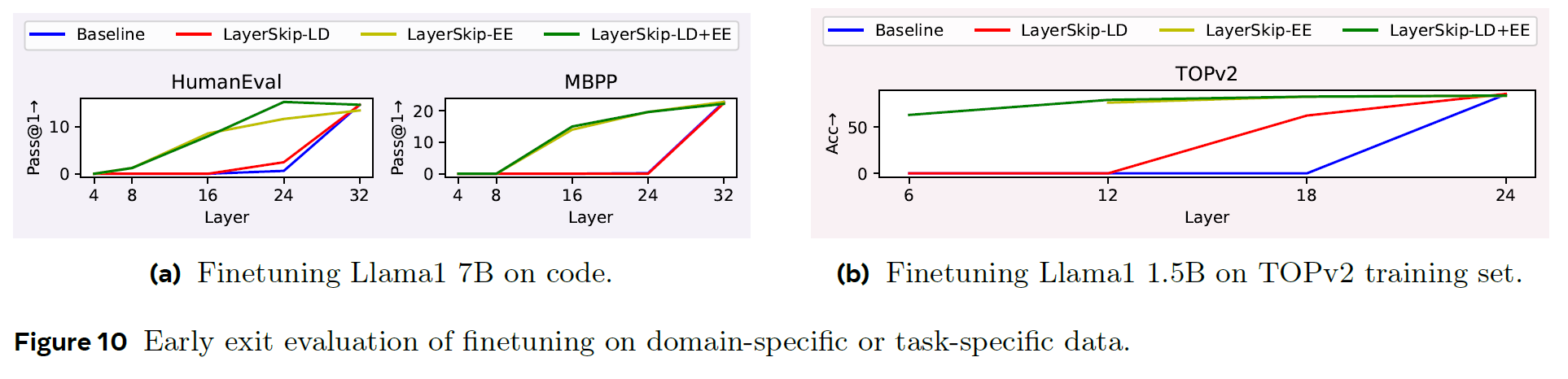
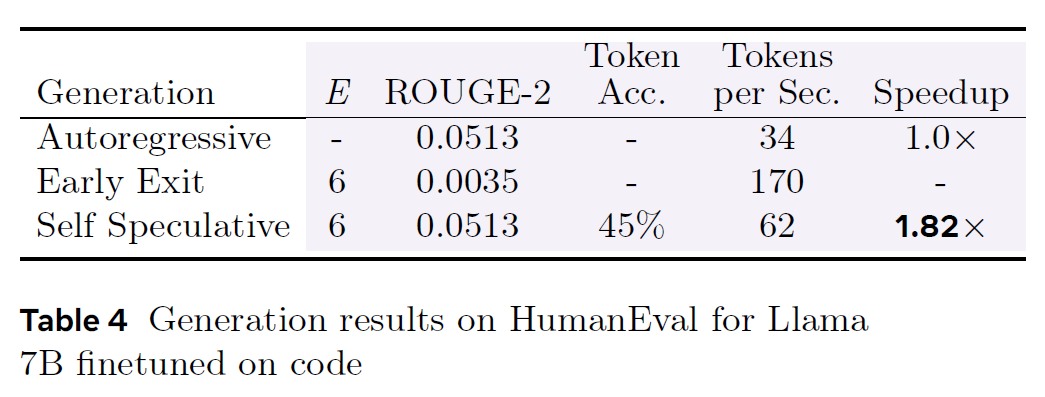
Finetuning on Code Data

• Fig 10a

• earlier layers are better than the baseline

• LD+EE shows a big improvement

• this is specific domain data, scaled $e_{scale}$ to 1.0

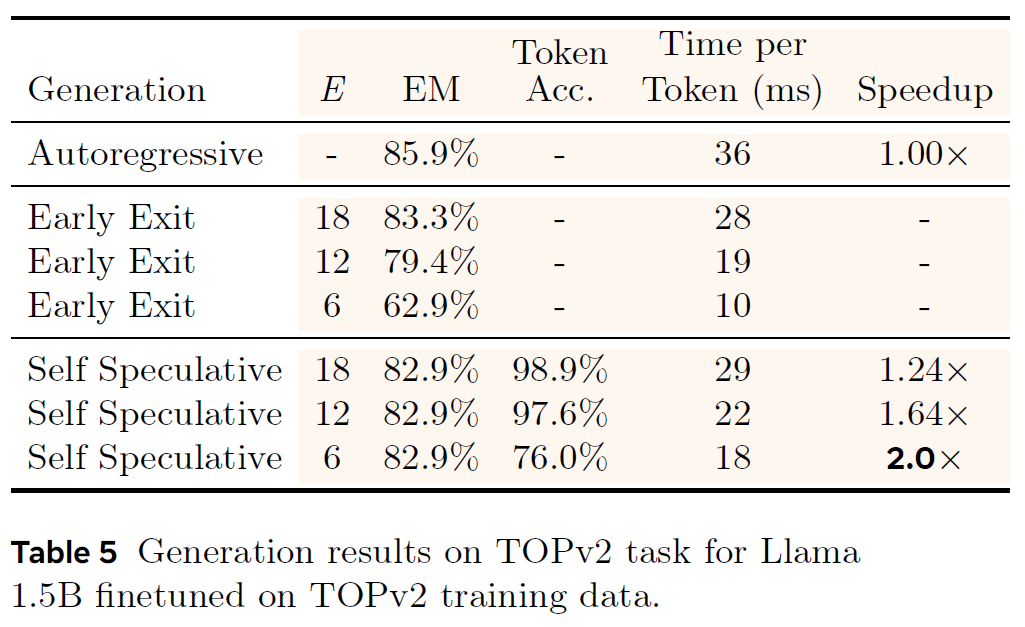
Finetuning on Task-Specific Dataset

• Fig 10b

• removing layers from the baseline, the model is not able to generate complete and accurate parses $\rightarrow$ 0 EM

• LayerSkip shows 77% at layer 12

• regression in the final layer reducing accuracy by 3%

6.2. Self-Speculative Decoding Results

• used EM, ROUGE-2

• compared with common models and tasks in Draft & Verify

• used greedy decoding and max 512 tokens

Continual Pretraining

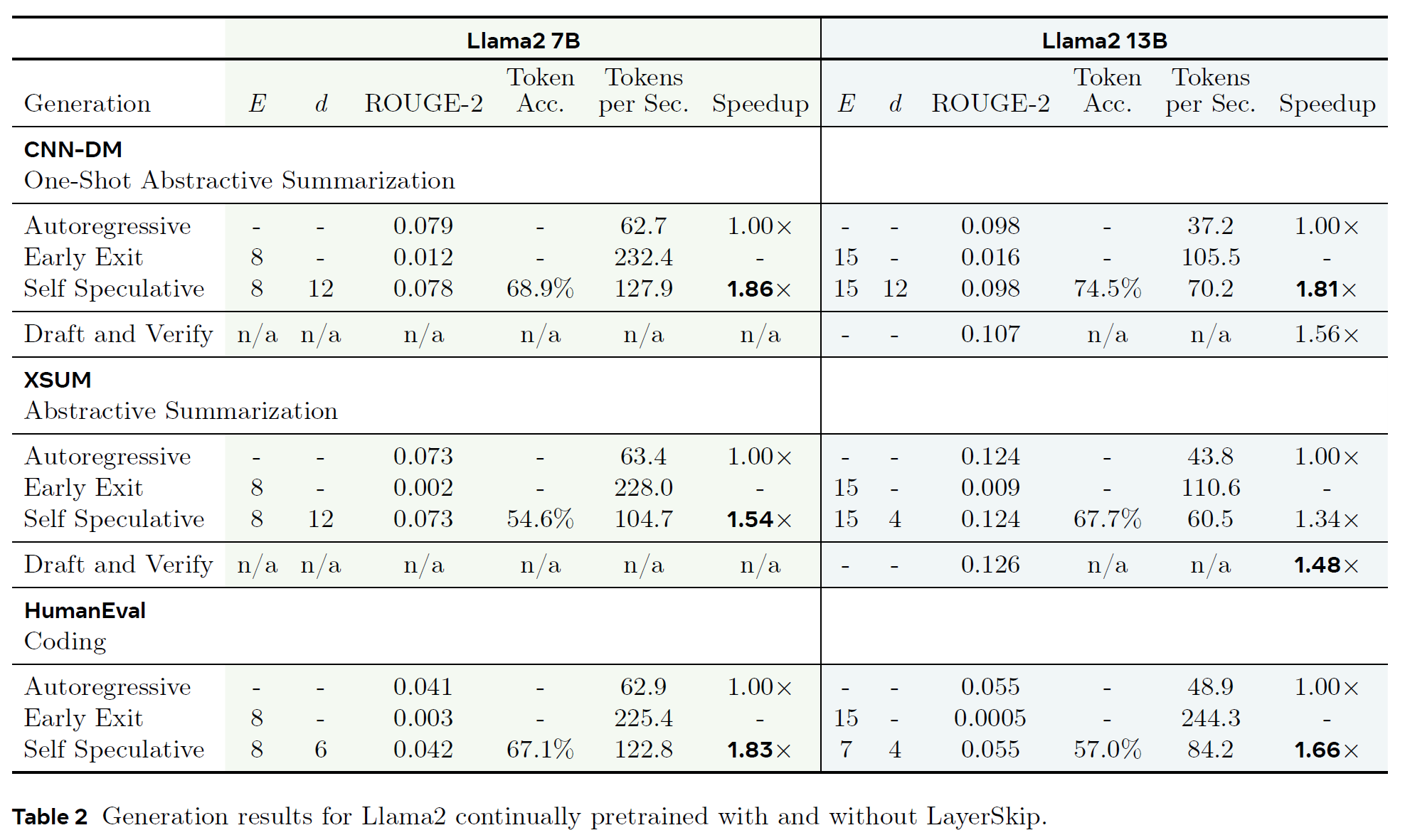
• higher speedups for the smaller model

Pretraining from Scratch

Finetuning on Code Data

Finetuning on Task-Specific Data

7. Ablation Studies

Scaling with Pretraining Tokens

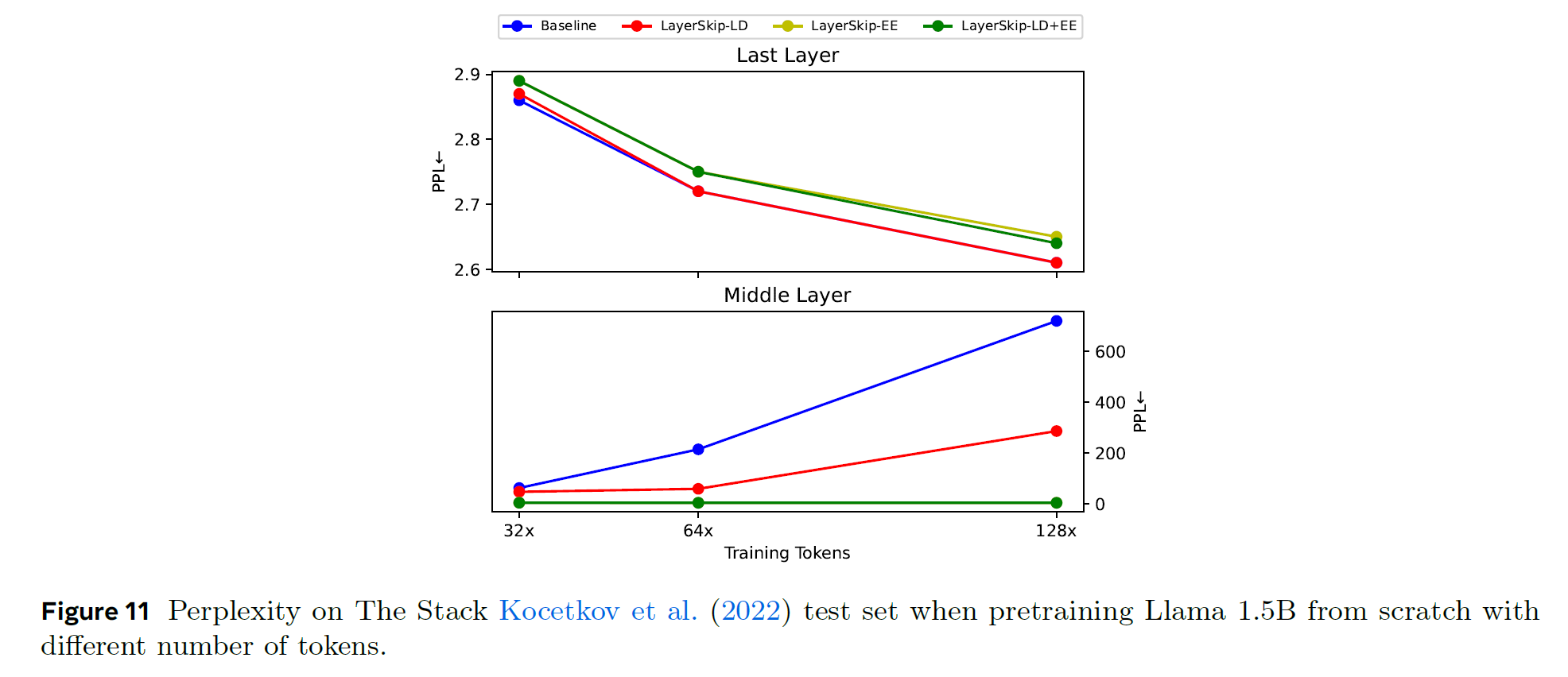
• 50000 steps

• batch size per device: 4

• context window: 4096

• number of GPUs: 32, 64, 128

• middle layer PPL increases by default (w/o EE)

• could open door about the dynamics of transformers

KV Cache in Self-Speculation

• use of KV cache is able to consistently save 9-20ms per token

8. Limitations

• self-speculative decoding doesn't require changing a model's weights

• $p_{max}$, $e_{scale}$, $R$ need to be tuned

• pretraining with layer dropout from scratch, increasing LR is needed and tuning LR is tricky

9. Conclusion

• layer dropout + early exit loss improves accuracy and speed

• hope this to be combined with PEFT

• in the future, increasing the accuracy of early-exit layers and exploring dynamic conditions to determine a different exit layer can be done

10. Comment

Pruning과 다르게 선택적인 레이어만 사용하여 학습과 추론을 하는 것, 그리고 남는 레이어를 이용해 Self-Speculative Decoding을 알차게 구현한 기법. Transformer에서는 결국 모든 레이어가 필요치 않은듯. CoT without prompting과 결이 비슷한 듯.