..?

1. Introduction

• Transformers require $\Omega(L)$ memory and compute to predict the next token of a sequence of length $L$ (using Flash Attention!)

• Attempts to make similar architectures but with $O(1)$ memory to predict each token $\rightarrow$ S4 or Mamba / RNN / models that can trained in parallel like linear attention / parallel RNNs

  • Say all models as GSSM (Generalized State Space Models)

• Resent work says GSSM's performance but it is not clear what these models sacrifice for efficiency

  • One particular capability that is sarificed is the ability to retrieve and repeat parts of the input context

• Theoritical analysis of copying task

  • Transformer can copy strings of length that is exponential in the number of heads of the transformer
  • Transformer implements a 'storage' mechanism and retrieval of sequences of n-grams
  • GSSMs cannot accurately copy strings with more bits than the size of the latent state

• In practice, large GSSM may have enough capacity to represent the entire input in the latent state

  • Transformers are both much more efficient at learning to copy and to generalize better to longer inputs
  • Copy algorithms learned by Transformers are based on n-grams to perform where to copy from

2. Theory: Representational Capaciy

2.1 Setting

• dictionary $\mathbb{D}$ which contains $D$ alphabet tokens

• seq2seq model $H : \mathbb{D}^* \rightarrow \mathbb{D}^*$

  • input $x_1, x_2, ... x_i$ as the prompt
  • $H(x_1, x_2, ... x_i)$ as the generated 'answer'

• sequence to token model $h : \mathbb{D}^* \rightarrow \mathbb{D}$

  • it naturally defines $H$ by autoregressive inference
  • for every input sequence $x_1, ... ,x_i \in \mathbb{D}$, define $x_{i+j} = h(x_1, ... ,x_{i+j-1})$ recursively and let $H(x_1, ... ,x_i) = (x_{i+1}, x_{i+2}, ... )$

GSSM

• Finite set $\mathcal{S}$ is a state space

• the number of bits required to encode the states of $\mathcal{S}$ as $\text{mem}(\mathcal{S}) = \log(|\mathcal{S}|)$

• GSSM is a sequence model defined by an update rule $u : \mathcal{S} \times \mathbb{D} \rightarrow \mathcal{S}$ and some output function $r : \mathcal{S} \rightarrow \mathbb{D}$

  • Let $s_o \in \mathcal{S}$ be some initial state
  • Given sequence $x_1, ..., x_L$, the state of model at iteration $i$ is denoted by $S_i(x_1, ..., x_i)$
  • the output token is denoted by $R_i(x_1, ..., x_i)$
  • The recursive process is
    $\begin{aligned} &1)\quad S_o(\empty) = s_0 \\ &2) \quad S_i(x_1, ... ,x_i) = u(S_{i-1}(x_1, ..., x_{i-1}), x_i) \\ &3) \quad R_i(x_1, ..., x_i) = r(S_i(x_1, ..., x_i)) \end{aligned}$

• Note that for any sequence model, there are two types of memory considerations

  • Input-Independent Memory - parameters
  • Input-Dependent Memory - activations

• GSSM definition constraints the input-dependent memory $\text{mem}(\mathcal{S})$

• It doesn't restrict in any way the amount of input-independent memory or the runtime of state updates

• Leaving all other considerations unconstrained shows the lower bownd on the state space memory

Transformers

• input length $L$

• dimension $d$

• input tokens $\boldsymbol{x}_1, ..., \boldsymbol{x}_L \in \mathbb{R}^d$

• an attention head is parametrized as $W_q, W_k, W_v \in \mathbb{R}^{d \times d}$

• $\boldsymbol{k}_i = W_k \boldsymbol{x}_i, \quad \boldsymbol{q}_i = W_q \boldsymbol{x}_i, \quad \boldsymbol{v}_i = W_v \boldsymbol{x}_i$

• $K_i = [\boldsymbol{k}_1, ..., \boldsymbol{k}_i] \in \mathbb{R}^{d \times i}, \quad V_i = [\boldsymbol{v}_1, ..., \boldsymbol{v}_i] \in \mathbb{R}^{d \times i}$

• the output of the head at token $i$ is $\boldsymbol{o}_i = V_i \ \cdot \ \text{softmax}(K_i \cdot \boldsymbol{q}_i) \in \mathbb{R}^d$

• with $l$ attention heads, the full dimension should be $dl$

• embedding $\Psi : \mathbb{D} \rightarrow \mathbb{R}^d$

• MLP $f : \mathbb{R}^{dl} \rightarrow \mathbb{R}^{dl} \ \text{s.t.} \ f(\boldsymbol{x}) = U_1 \sigma (U_2 \boldsymbol{x})$

• embedding and MLP is applied on the token level

• Attention-block is a set of $l$ heads applied in parallel

• transformer-block is an attention-block floowed by an MLP on the concatenated output of $l$ heads

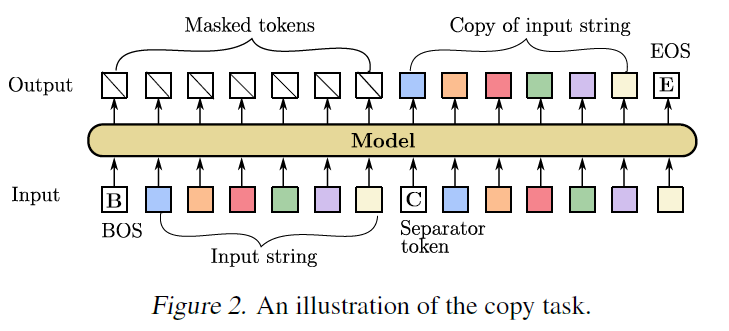
The Copy Task

• Add two special token <BOS> and <COPY> to $\mathbb{D}$
  • $|\mathbb{D}| = D + 2$
• A length-$L$ copy distribution $\mathcal{D}_L$ over $\mathbb{D}^{L+2}$ generates strings of the form "<BOS>, $x_1, x_2, ..., x_L$, <COPY>" where $\boldsymbol{x} \in (\mathbb{D} \text{\textbackslash} \{ \tiny \text{<BOS>},\text{<COPY>} \normalsize \} )^L$
• For some seq2seq model $H$, denote the error of $H$ on a copy distribution
  $\text{err}_{\mathcal{D}_L}(H) = \underset{\mathcal{D}_L} {\text{Pr}}[H_{1:L}(\tiny \text{<BOS>} \normalsize, \boldsymbol{x}, \tiny \text{<COPY>} \normalsize) \not= \boldsymbol{x}]$

2.2 Transformers can copy inputs of exponential length

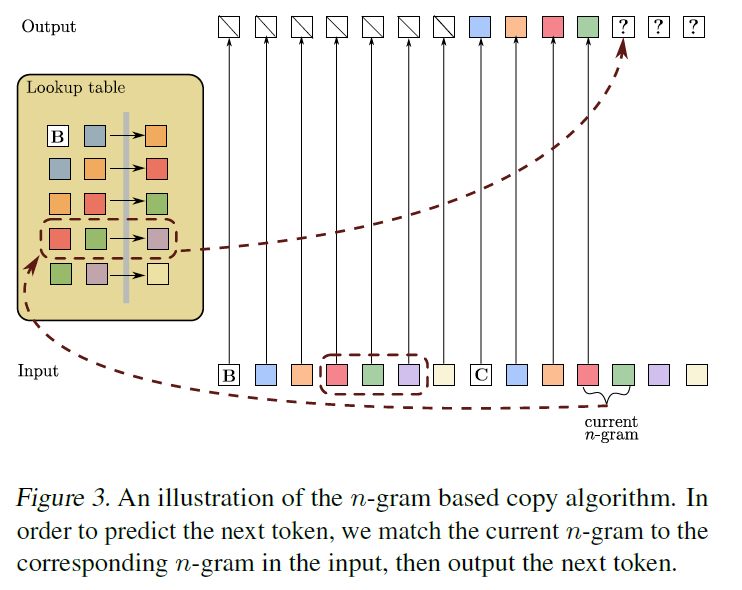
Construction : Hash-Based Copying

• Hash sequences of $n$ tokens
• At each iteration of the auto-regression attend to the previous occurrence of the most recent $n$-gram and output the succeeding token
  
  
  

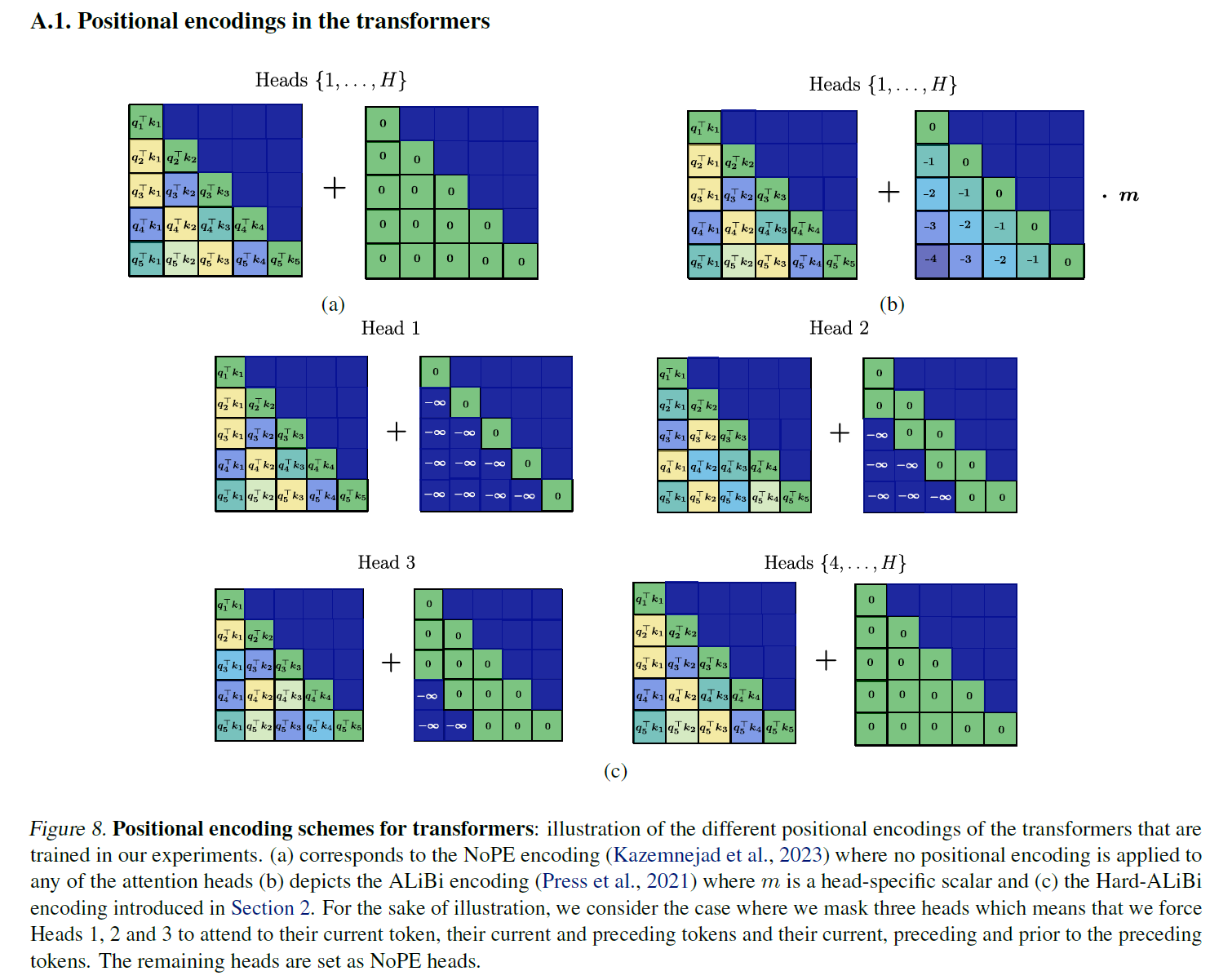
Positional Embedding: Hard-ALiBi

• To perform the hashing described in the algorithm, it is necessary to leverage local positional information to define a hash and apply it globally on the entire input $\rightarrow$ use Hard version of ALiBi

• Alibi : biases the attention scores with a penalty that is proportional to their distance ($m$ is a head-specific slope fixed before training)

• add a bias $b_i$ to the $i$-th attention head

  • $\boldsymbol{o}_i = V_i \ \cdot \ \text{softmax}(K_i \cdot \boldsymbol{q}_i + b_i)$
  • $b_i = \begin{cases} b_{i, j} = - \infin \quad &j \le i-m \\ b_{i,j} = 0 \quad &j > i-m\end{cases}$
  • Allow different head with different $m$ and also allow $m = \infin$ (softmax attention with no PE)
    

Guarantees

• The copy algorithm can perfectly copy the input sequence, as long as there are no repeated $n$-gram patterns in the input
• Then the error of the algorithm is
  $p_{\text{n-gram}}(\mathcal{D}_L) = \underset{\mathcal{D}_L}{\text{Pr}} [\exist_{i \not= j} \ \text{s.t.} \ x_1, ..., x_{i+n} = x_j, ..., x_{j+n}]$

Theorem 2.3.

For all $n$, there exists a depth-2 transformer $\mathcal{T}$ of dimension $O(n \log (D))$ s.t. for all $2n \le L \le D^n$ and for any copy distribution $\mathcal{D}_L$, $\text{err}_{\mathcal{D}_L}(\mathcal{T}) < p_{\text{n-gram}} (\mathcal{D}_L)$

• The probability of repeated $n$-grams quickly decays when $n$ increases
• For the uniform distribution over sequences, thie probability decays exponentially witn $n$

Lemma 2.4.

Let $\mathcal{D}_L$ be the copy distribution generated by sampling $\boldsymbol{x}$ from the uniform distribution over the non-special (alphabet) tokens. Then $p_{\text{n-gram}}(\mathcal{D}_L) < L^2D^{-n}$

• By combining those, we get that Transformers can copy sequences of tokens drawn from the uniform distribution using a number of params that depends only logarithmically on the input sequence length

Corollary 2.5.

Fix some $\epsilon \in (0, 1/2)$ and some $L \ge \Omega(\log (1/\epsilon))$, there exists a depth-2 Transformer $\mathcal{T}$ of dimension $O(\log(L/\epsilon)\log(D))$ s.t. for the uniform copy distribution $\mathcal{D}_L$, $\text{err}_{\mathcal{D}_L}(\mathcal{T}) < \epsilon$

• This doesn't limit the precision of the parameters of activations, but it holds for finite-precision transformers, using $O(\log(\log(L)))$ bits
  

2.3 State Space Models cannot copy inputs beyond memory size

• GSSMs cannot copy uniform input sequences unless the capacity of their state space grows linearly with the sequence length (To be able to copy, the model needs to store it in state space)

Theorem 2.7.

Fix some GSSM $H$ over state space $\mathcal{S}$. Then for all $L$, for the uniform copy distribution $\mathcal{D}_L$, the model $H$ has error $\text{err}_{\mathcal{D}_L}(H) > 1 - {|\mathcal{S}| \over {D^L}}$

Corollary 2.8.

Fix some $L$ then every GSSM $H$ with state space $\mathcal{S}$ s.t. $\text{mem}(\mathcal{S}) < L \log (D) - 1$ has error $\err_{\mathcal{D}_L}(H) > 1/2$ for uniform copy distribution $\mathcal{D}_L$

• The Input-dependent memory of Transformers grows linearly with the sequence length (less memory-efficient than GSSM)
• Transformers are almost optimal in terms of input-dependent memory (at least copying)
• Thm 2.3. says that there exists a transformer which can copy inputs of length $L$ using $\tilde{O}(L)$ input-dependent memory and it is optimal by Corollary 2.8.

3. Learning to Copy

• Above results may not be observed in practice
  • It's not clear that transformers can indeed learn to copy from examples
  • In practice, GSSM may use a large latent state memory so that this bounds only hold for very long sequences of tokens (Also, it may not learn to do so)

3.1. Experimental Setup

• Transformer and Mamba $\approx$ 160M
• LSTM $\approx$ 40M
• 64 Batch
• 10 batches of 128 examples for test
• token space size is 30 and normally $\mathcal{V} = \{a, ..., z, \tiny \text{<BOS>}, \text{<EOS>}, \text{<COPY>} \normalsize \}$
• All strings are sampled uniformly
  • sample the length of the sequence
  • independently sample each position of the string from $\mathcal{V}$
  • pack the context with i.i.d. sequences during training
  • fill the context with multiple independent samples of task
• Positonal Information
  • RoPE
  • NoPE (No Positional Information)
  • Hard-ALiBi

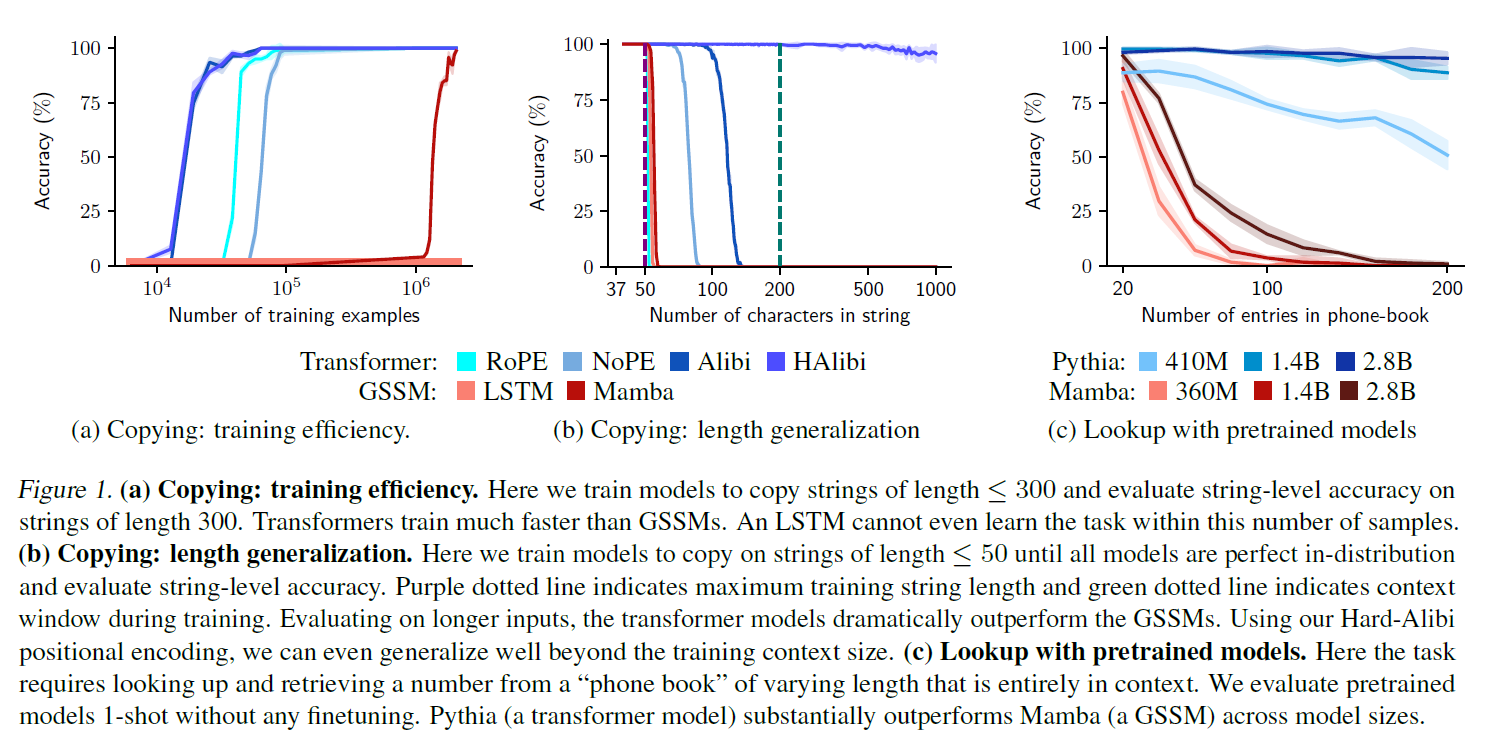
3.2. Data Efficiency on the Copy task

• Model gets an input of $\le L \le 300$ tokens followed by separator token
• record the string-level accuracy
• sharp change is due to the log-scaled x-axis and string-level accuracy as a y-axis
• String-level Accuracy
  
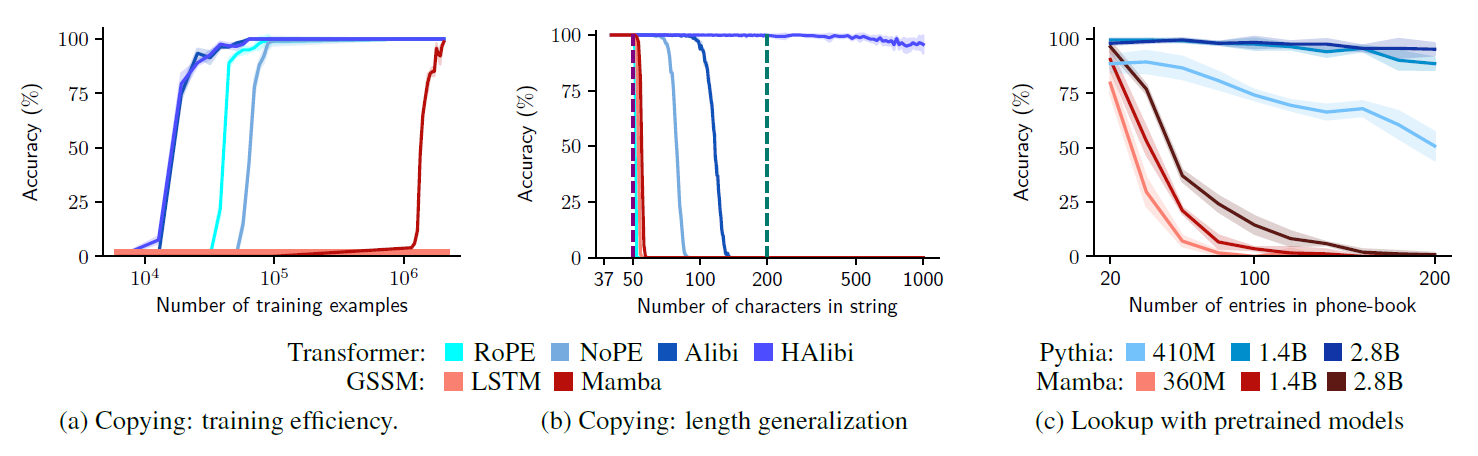
• Character-level Accuracy
  

3.3 Length Generalization on the Copy Task

• Test to generalize out-of-distribution

• Understand which function the model has learned

  • model has truly learned the "correct" copy operation vs it just learned to copy sequences of the particular size it was trained on

• Trained all models on sequences of $\le 50$ tokens test them up to 100 tokens (string-level accuracy)

• Transformers shows better generalization to longer input compared to GSSMs

  • GSSMs' performance drops to near zero
  • ALiBi and NoPE dramatically outperform the RoPE
  • Sinusoidal embedding of RoPE creates a more dramatic change thatn the decay of ALiBi or NoPE

• Using Hard-ALiBi in sequence length less than 50 shows almost perfect generalization up to 1000 tokens

3.4. Transformers learn to use n-gram hashing

• To test whether the transformer uses the storage mechanism and retrieval of n-grams

• Train Hard-ALiBi Transformer on the copy task with a dataset contains duplicate n-grams

• Draw uniform sequences of tokens and randomly replace some n-gram with another n-gram that already appears in the sequence (each example always have two copies of n-gram)

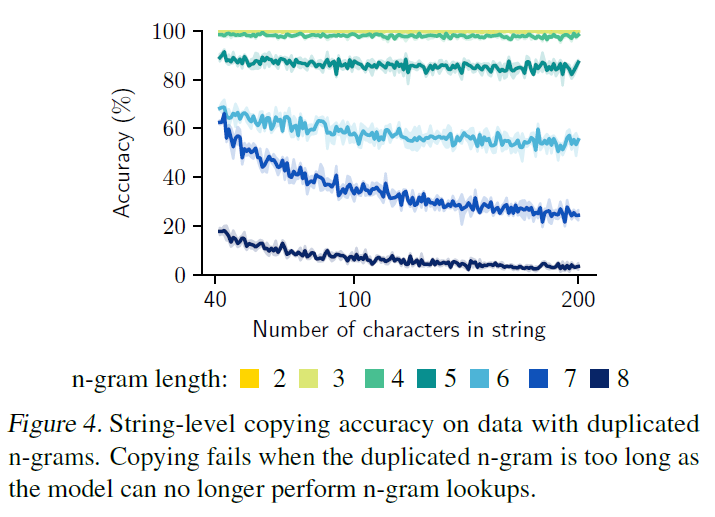
• It seems Transformer relies on something like 5-gram retrieval to do the copy task

3.5. GSSMs cannot arbitrarily retrieve from context

• n-gram lookup task : the model should use given n-gram as a key to loop up k-token key that follows the query

  • suffix key and prefix key
  • assess length generalization
    

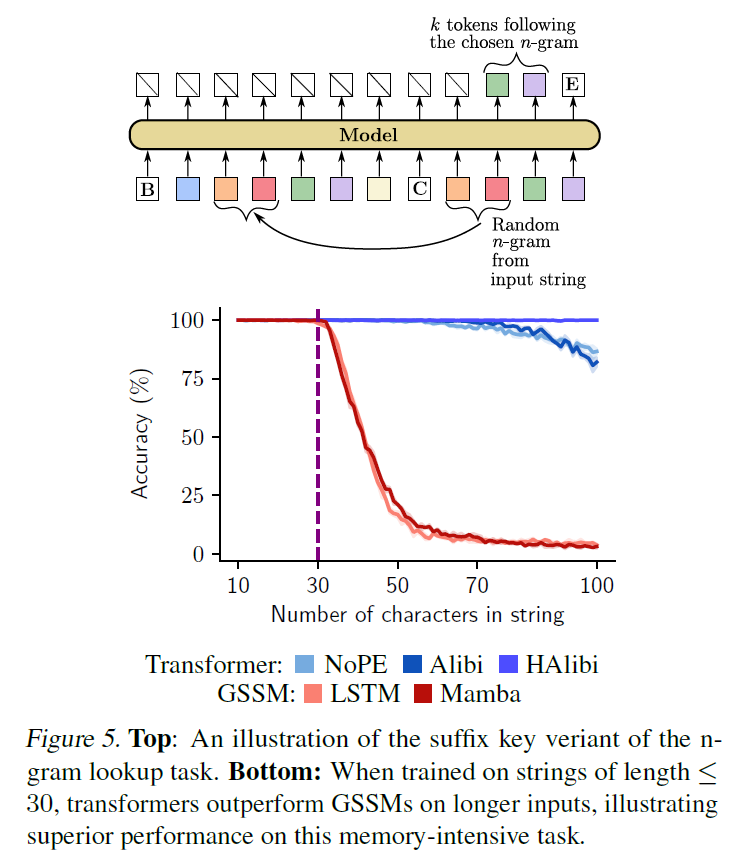
• Suffix key version

  • given sequence $L$ of input tokens, separator, n-gram from the input sequence
  • need output sequence of $k$ tokens following the chosen n-gram
  • it requires the model to be able to 'store' the context to find the correct key
  • train all models on sequences of at most 30 tokens
  • Transformers perform well
  • Transformers learn to n-gram retrieval and storage
    

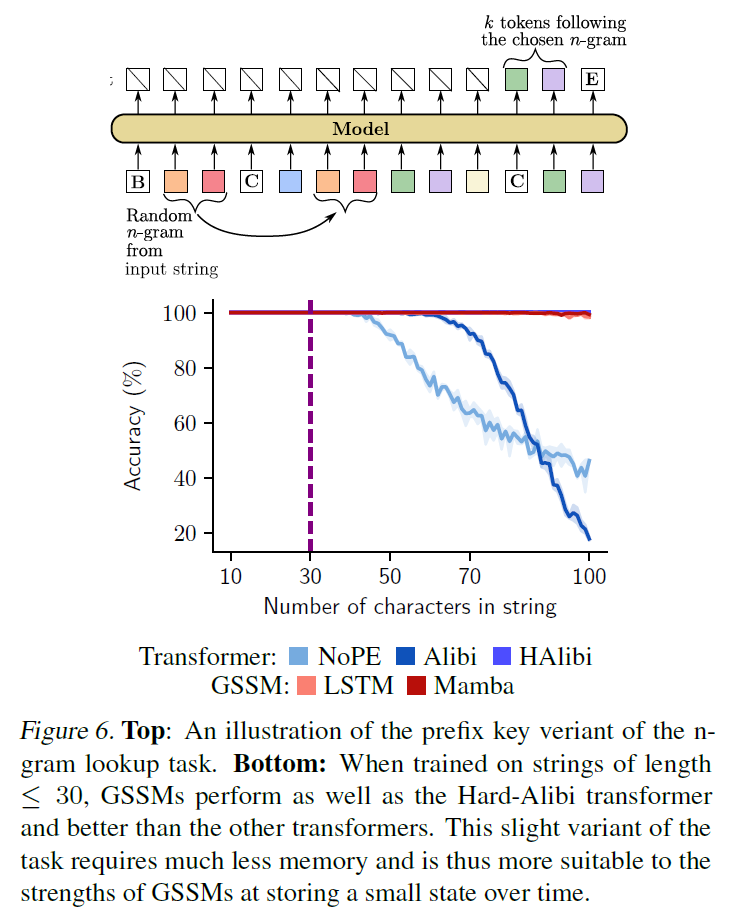
• Prefix key version

  • provide n-gram key at the beginning and then the full sequence
  • model doesn't have to store the entire input as it can find the key on the fly
  • good for the GSSMs since they can write the key in to the state and then ignore inputs that don't match
  • GSSMs achieved almost perfect (outperformed NoPE and ALiBi but Hard-ALiBi)
  • This may be an issue where positional embedding make it more diffecult to perform the hashing lookup over a long distance
  • GSSM is memory limited but effective when the tasks only require a summary of the inputs

4. Pre-trained Models

• pretrained Transformer, GSSM
• copying long strings, retrieval and few-shot QA
• Transformer outperforms GSSM even GSSM shows lower PPL

4.1. Setup

• Pythia transformer models 410M ~ 2.8B

• Mamba with similar size

• Pretrained on Pile, used same tokenizer

• Copy based task / Information Retrieval (selective copy)

• String-Level Accuracy

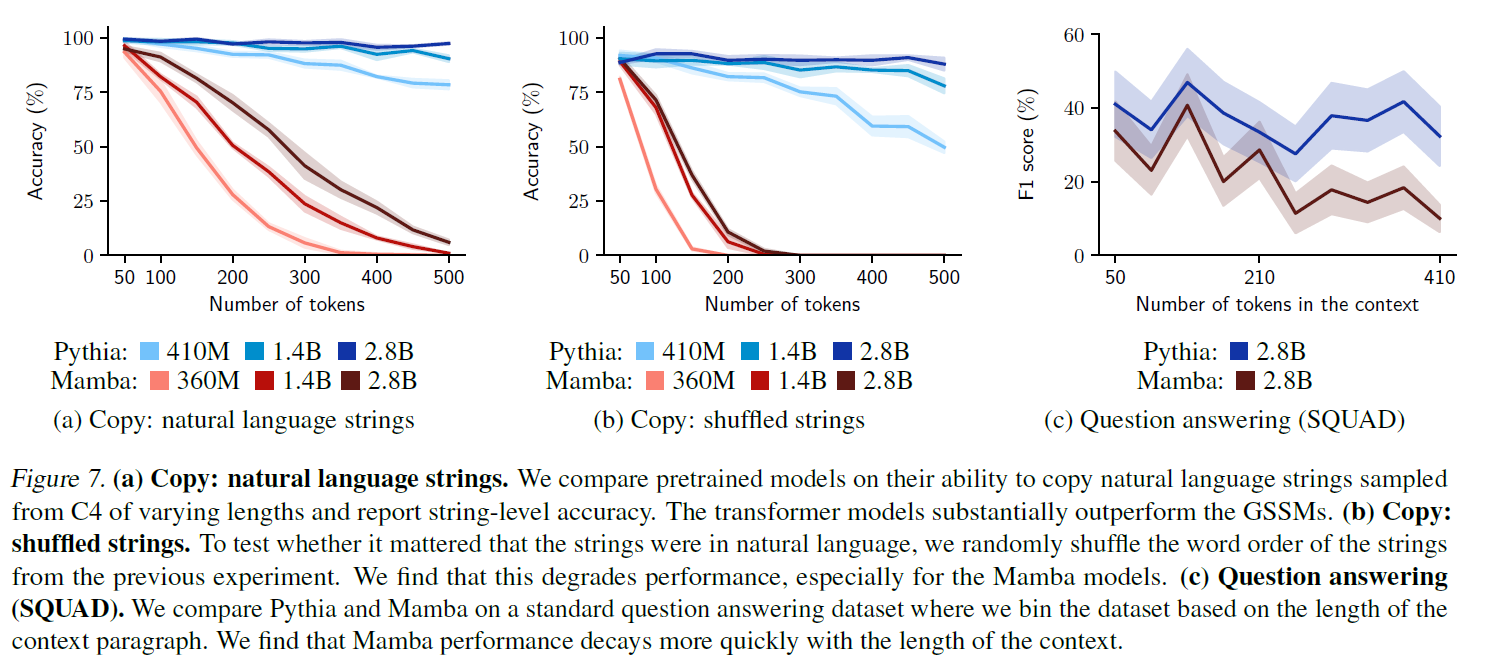
4.2. Copying the input text

• Transformers > GSSM
• Random sample from C4 dataset
• two copies of sampled string + first word of the string $\rightarrow$ complete the third copy
• Unlike random string, natural text can often be compressed so that the model use lower memory to copy
• When the input is more difficult to compress, GSSM suffers due to its state size

4.3. Retrieval from the input context

• Phone-book Lookup

  • provide a synthetic phone-book to the model ans ask it to return the phone number
  • randomly sampling $L$ names and phone number
  • two-shot examples and question for phone-number
  • Transformer (410M) > GSSM (2.8B) when $L \ge 70$

• QA

  • 2.8B Mamba and Transformer on SQuAD
  • provided single demonstration of a QA pair with same text
  • Mamba degrades more quickly with the paragraph length

5. Discussion

• Transformer > GSSM at copying from their input text

• SSM have many advantages over transformers

  • The memory and computational complexity doesn't increase with the input length $\rightarrow$ good for long context
  • Better at tracking state variables across long sequences to make long consistent text
  • Similar to Human brain

• Future work is needed to make hybrid architectures of SSM and attention-like mechanism to enhance retrieving ability

  • Humans have very limited memory but can translate entire novels if we allow look back at the text

6. Comment

제목이 자극적이었음. Retrieval 부분에서 Transformer의 성능을 증명했음. 다른 분야보다도 텍스트 관련해서는 이 점 때문에 SSM의 도입이 쉽지는 않을듯