1. Introduciton

• Increased Scale is one of the main drivers of better performancd in DL (NLP, Vision, Speech, RL, Multimodal etc.)

• Most SOTA Neural Nets are trained from-scratch (random weights) $\rightarrow$ Cost for training is high

• Model Upcycling: upgrading an existing model with a relatively small additional compulational budget

  • focus on dense models into larger sparsely activated MoEs (pretrained dense Transformer checkpoint)
  • less than 40% additional budget for all size for language and vision

• Valuable in two scenarios

  • Have access to a pretrained Transformer and want to improve it within a computational budget
  • Plan to train a large model and don't know whether dense of MoE would be more effective $\rightarrow$ First train the dense model then upcycle it into a MoE

• Central challenge in model upcycling is the initial performance decrease entailed by changing a trained network structure $\rightarrow$ present a model surgery recipe

2. Background

2.1 Sparsely Activated Mixture of Experts (MoE)

Dense vs Sparse

• Dense model : apply all params to every input
• Sparse model : activating a subset of params for each input
• MoE models are an accelerator friendly family of sparse models that allow training of models with up to trillions of params

MoE Model

• alternate standard Transformer blocks with MoE blocks
• usually replace the MLPs in a Transformer block with a number of 'experts' (also MLP) with different params and a router (small neural net, decides which expert should be applied)
• There is multiple routing algorithms (Top-K, BASE and Sinkhorn-BASE layers, Hash layers, Expert Choice routing)

Sparsely Gated MoE (Shazeer et al., 2017)

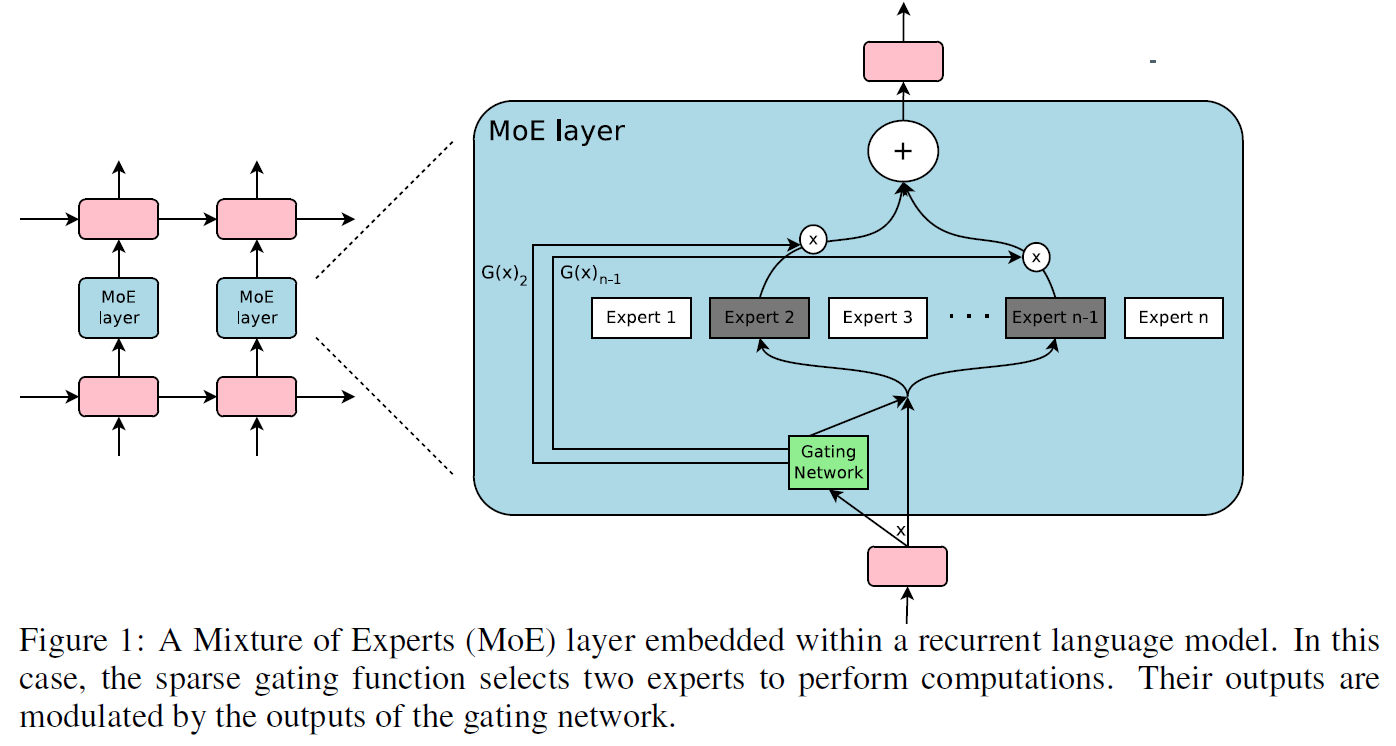
• Gating network $G(x) \in \mathbb{R}^n$ and $n$ expert networks $E_1, E_2, ... E_n$
• the output $y$ of the MoE module is $y = \sum_{i=1} ^n G(x)_i E_i(x)$
• $G(x)$ is a sparse vector. This has only non-zero element in the index of selected expert
• The choice of gating function

  • Softmax gating : $G_{\sigma}(x) = Softmax(x \cdot W_g)$ where $W_g$ is trainable weight matrix

  • Noisy Top-K gating

    $\begin{aligned} G(x) &= Softmax(KeepTopK(H(x), k)) \\ H(x)_i &= (x \cdot W_g)_i + StandardNormal() + Softplus((x \cdot W_{noise})_i) \\ KeepTopK(v, k)_i &= \begin{cases} v_i \quad &\text{if } v_i \text{ is in top } k \text{ elements of } v \\ -\infin &\text{ otherwise } \end{cases} \\ Softplus(x) &= \ln ({1 + e^x}) \end{aligned}$

Expert Choice routing (Zhou et al., 2022)

• $E$ for total # of experts
• $n$ for total number of tokens
• Router output $\bold{R} \in \mathbb{R}^{n \times E}$ : routing probabilities
• the row $r_{i} \in \mathbb{R}^E$ corresponds to the $i$-th token and distribution over experts (non-negative and sum to 1)
• Every expert $e$ independently chooses the $T$ tokens with highest probabilities (top-T per column) and process
• parametrize $T$ as $T = C(n/E)$ where $C$ is a capacity factor to control # of tokens per expert (if $C=1$, some token will be processed by multiple experts while others by none)
• This makes a model parameter count increase with minimal FLOPs overhead (router computation)
• Letting $C > 1$ usually leads to higher performance at a higher compute cost
  
• $S = Softmax(X \cdot W_g), \quad S \in \mathbb{R}^{n\times e} \\ G,\ I = TopK(S^T, k), \quad P = Onehot(I) \in \mathbb{R}^{e \times k \times n}$
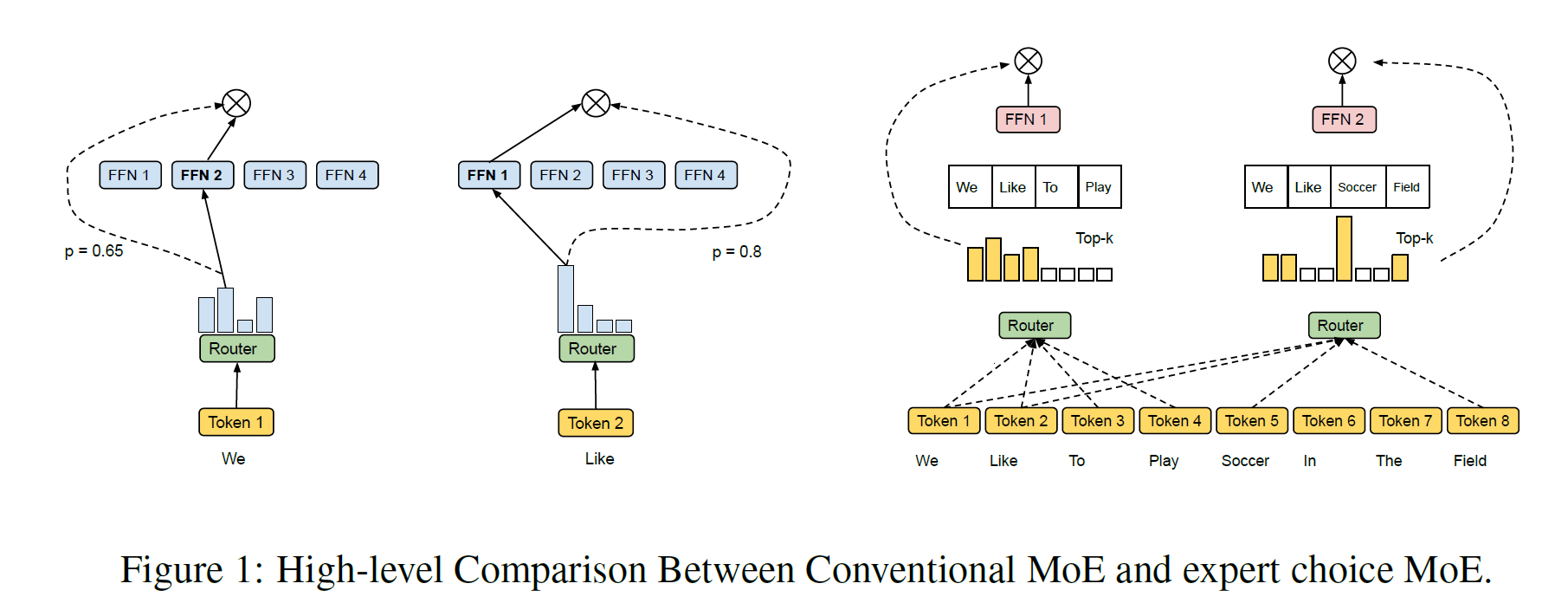
• $G \in \mathbb{R}^{e \times k}$ is for weight of expert for the selected token, $I$ is an index matrix where $I[i,j]$ = $j$-th selected token of the $i$-th expert
• Then, apply MoE and gating funtion in the dense FFN layer
  • input : $X_{in} = P \ \cdot \ X \in \mathbb{R}^{e \times k \times d}$ where $P$ is permutation matrix
  • $X_{in}[i] \in \mathbb{R}^{k \times d}$ is input for $i$-th expert
  • output of each expert
    $X_e[i] = \text{GeLU}(X_{in}[i] \cdot W_1[i]) \cdot W_2[i]^T$
  • Final output $X_{\text{out}}[l,d] = \sum_{i,j}P[i, j, l]G[i, j]X_e[i, j, d]$
    $l$ for batch dimension, $d$ for model dimension

2.2 Architectures

• Apply same sparse upcycling recipe to both language and vision tasks on T5 and ViT (encoder)
• ViT : follow V-MoE, but used global average pooling and Expert Choice Routing
• T5 : use Expert Choice Routing for encoder, Top-K routing for decoder with $K=2$

3. The upcycling Algorithm

Initialize

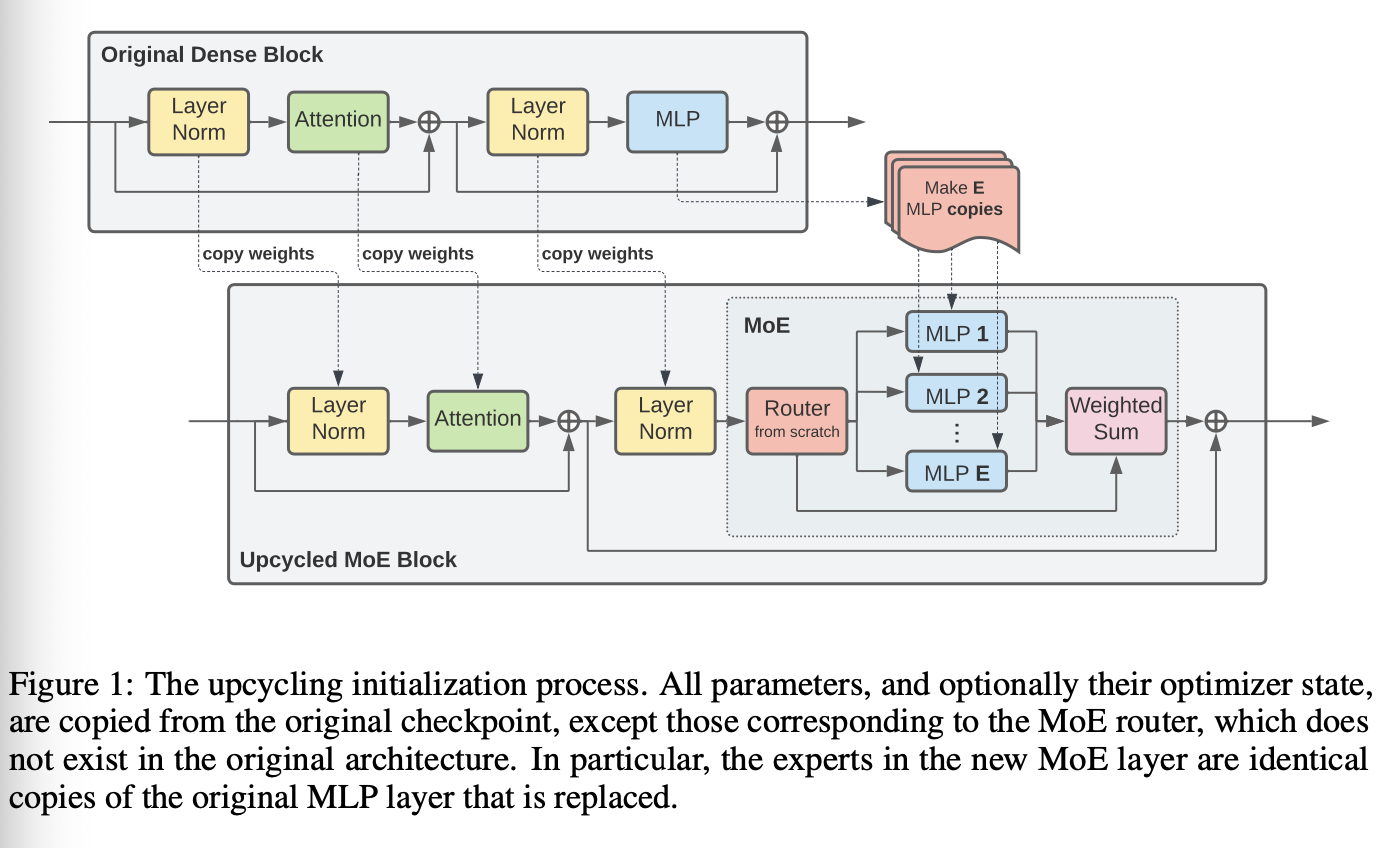
• Use dense model's parameters (checkpoint) to initialize new Transformer block (same number and shape)
• A subset of the MLP layers are expanded into MoE layer
• remaining layers are copied to new model
• each MoE have a fixed number of experts
• each expert is initialized as a copy of the original MLP
• After initializing, continue training it for a number of additional steps (considering budget and resources)

Design Decisions

The performance of upcycled models is heavily influenced by the configuration of the MoE layers

Router Type

• ViT : Expert Choice routing with $C=2$ (encoder)
• T5 : Expert Choice routing with $C=2$ (encoder), Top-K routing with $K=2$ (decoder)

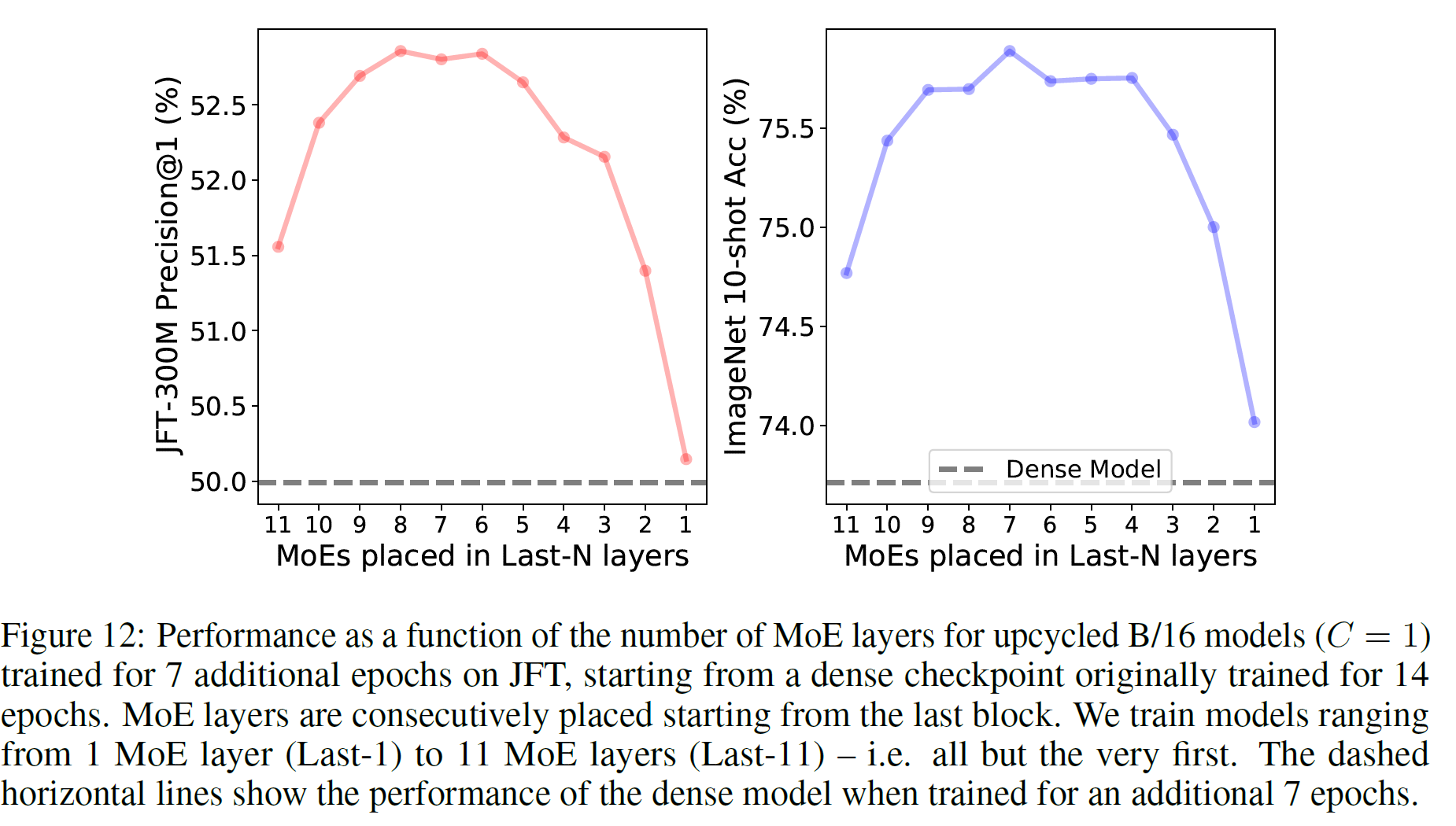
Number of layers to upcycle

• Adding more MoE increases the model capacity
• replace half of the MLP layers of original model with MoE layers

Number of Experts to add in upcycled layers

• Adding more experts doesn't significantly affect the FLOPS (the expert capacity is inversely proportional to the number of experts)
• Too many experts make the upcycled model's larger initial quality drop (this will be overcome by sufficientl upcycling compute)
• 32 experts was good

Expert capacity

• Larger Expert Capacity generally yields larger quality byt increases the FLOPS
• $C=2$ was good

Resuming Optimizer State (Vision)

• reusing the optimizer state gives a performance boost for vision models (not language)

Normalize weights after routing (Vision)

• To reduce the performance drop when upcycling model surgery, normalized the router combine weights of each token to 1
  • Each token was previously only processed by a single expert (original dense model)
  • for vision, it was helpful but it hurts the performance of language case. (the hypothesis that the decoder of T5 uses Top-K routing)

4. Experiments

4.1 Experimental Setup

• Vision : V-MoE, ImageNet using 10-shot, 5 different training sets, average accuracy
• Language : span corruption task on English C4 (pretrain), a proportional mix of all SuperGLUE (fine-tune), dense baseline starting checkpoint (Base), T5 1.1 checkpoints (L, XL)

4.2 Results

4.2.1 Core Result

Pretraining

• When applying small amount of Extra training, the performance is almost their original checkpoint
  

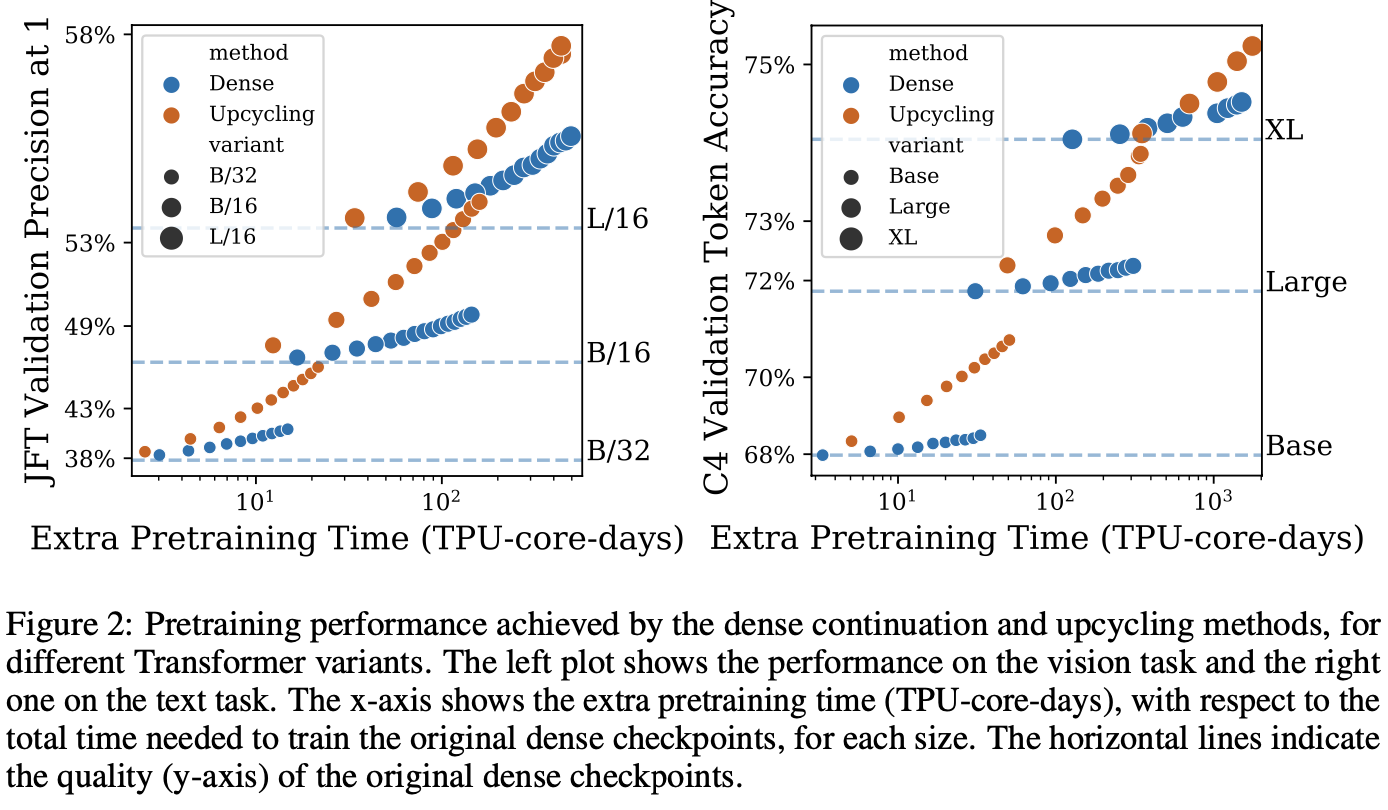
Full Fine-Tune

• Still, the upcycled model has faster growth of score
• For language, the difference is larger
  

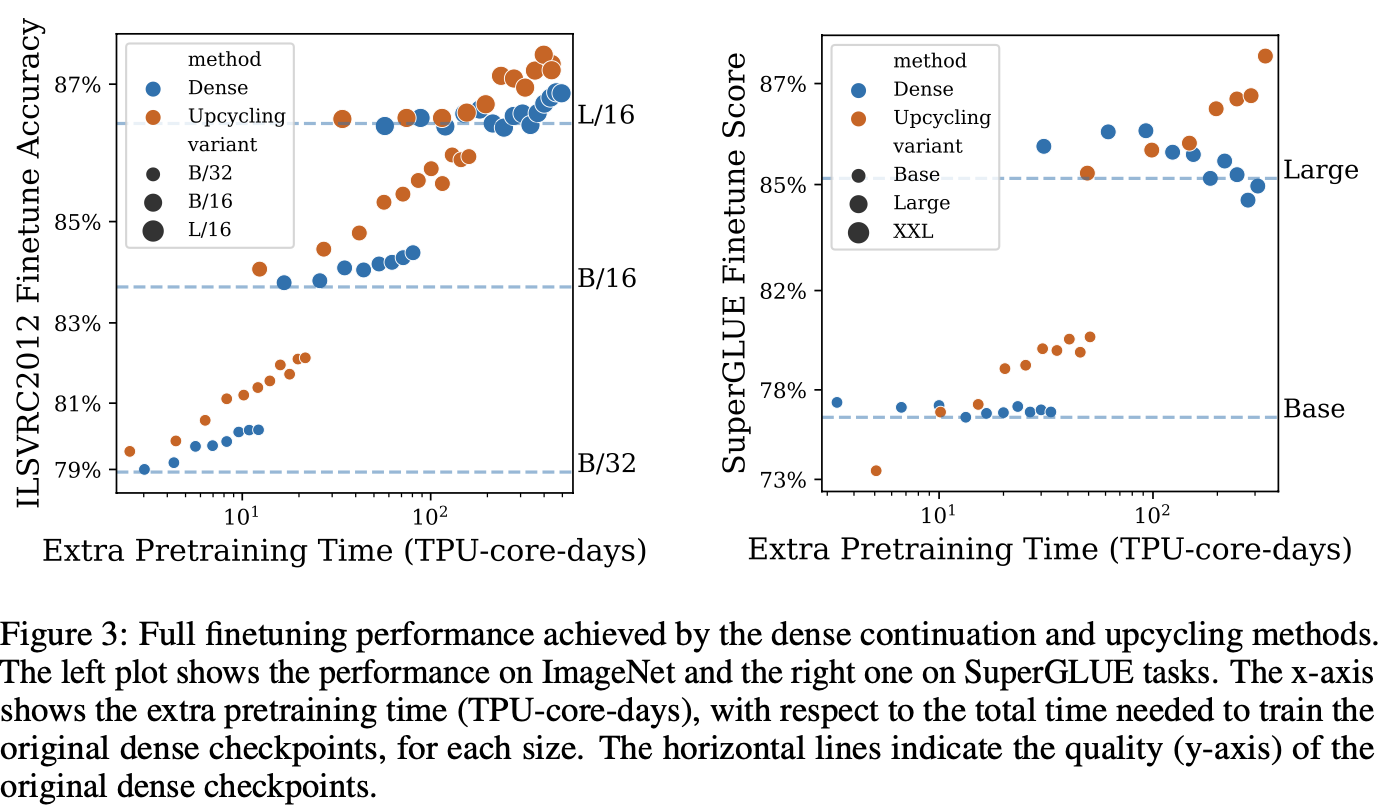
Sparse upcycling vs Sparse models from scratch

• training from scratch takes longer to catch up with the upcycled models
• For language, it used 120% of original dense checkpoint's computation to catch up upcycled models
• Larger learning rate + experts can develop and diversify from the beginning
• Given Large computation budget (> 100% of original dense), training MoE from scratch may be preferable
  

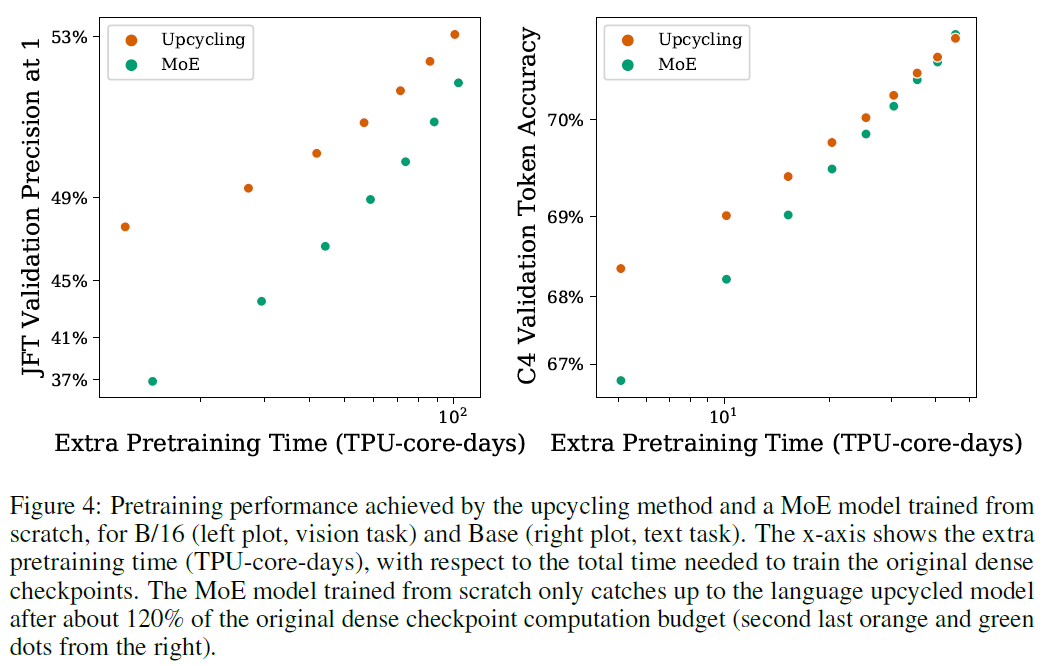
Sparse upcycling vs Warm starting

• Dense upcycling (depth tiling) replicates layers from dense Base checkpoint to construct new layer
  

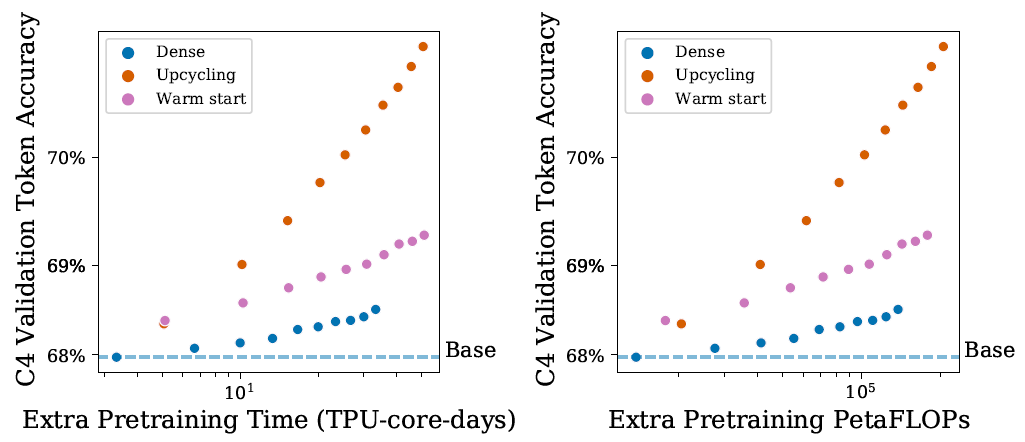
4.2.2 Ablations

• Vision : B/16 sparse model with 32 experts, $C=1$, 6 MoE layers at the last few blocks, dense checkpoint with 14 epochs + 7 additional epoch
• Language : Base with 32 experts, $C=2$, 6 MoE layers interspersed, 0.5M ~ 1M additional steps

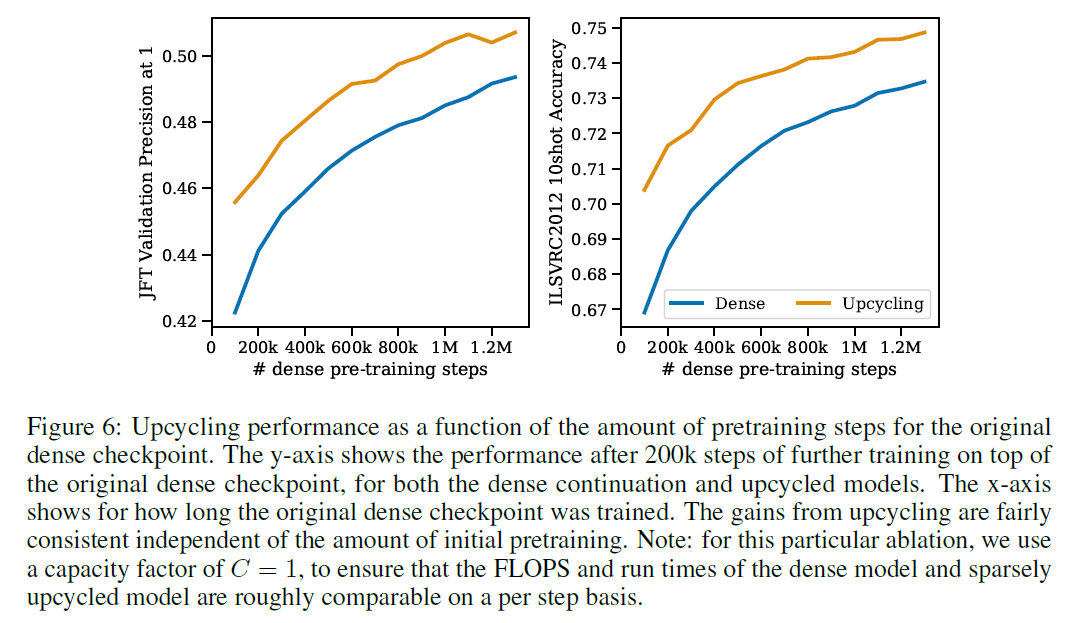
Amount of dense pretraining

• Regardless of the amount, upcycled model showed higher performance
  

Router type

• For vision, Top-K routing and Batch Prioritized Routing matches performance of Expert Choice Routing but slightly slow (step basis)
• Top-K underperforms Expert Choice routing per time basis
  

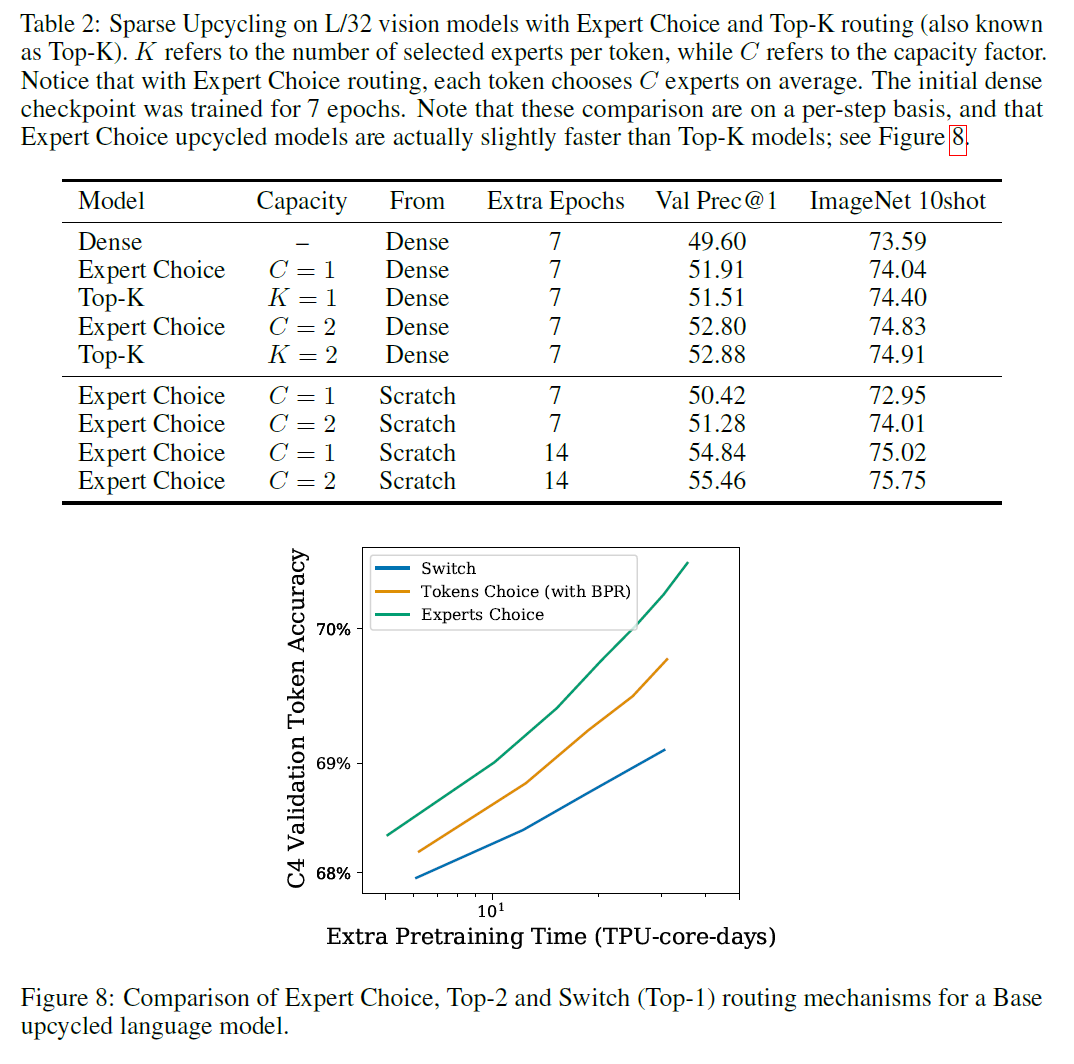
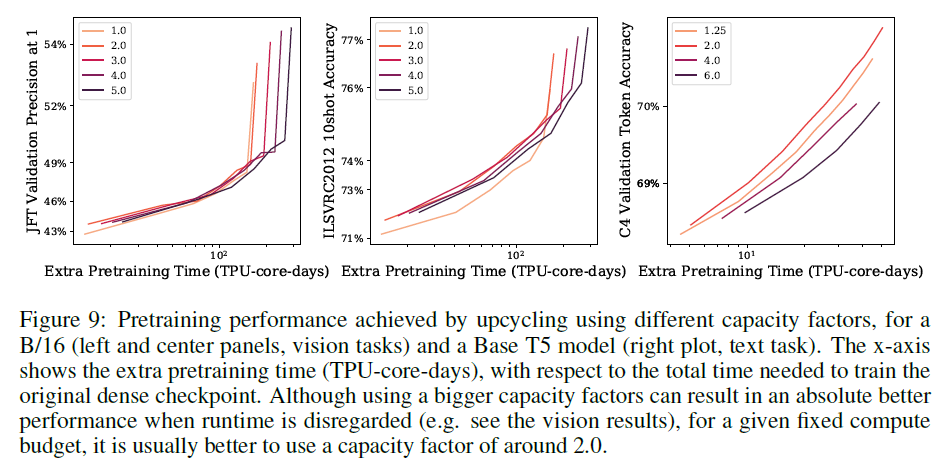
Expert Capacity Factor

• The more tokens processed by expert, the greater the computation and performance
• $C=2$ was best
  

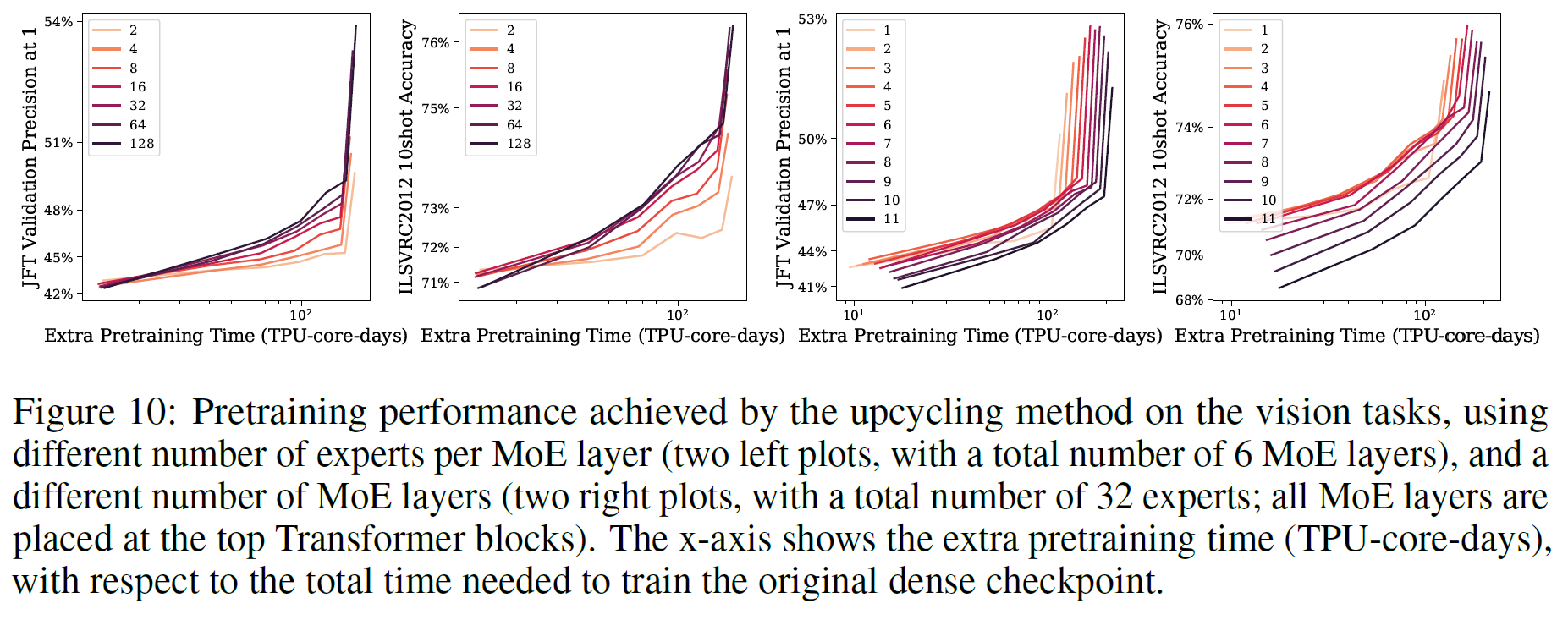
Number of MoE layers

• More MoE layers is not always better even on a per step basis
  
  

Initialization of Experts

• copying MLP layer >> train from scratch
• adding small Gaussian noise to each copied MLP layer didn't work (small amount - no effect, large amount - hurts the performance
  

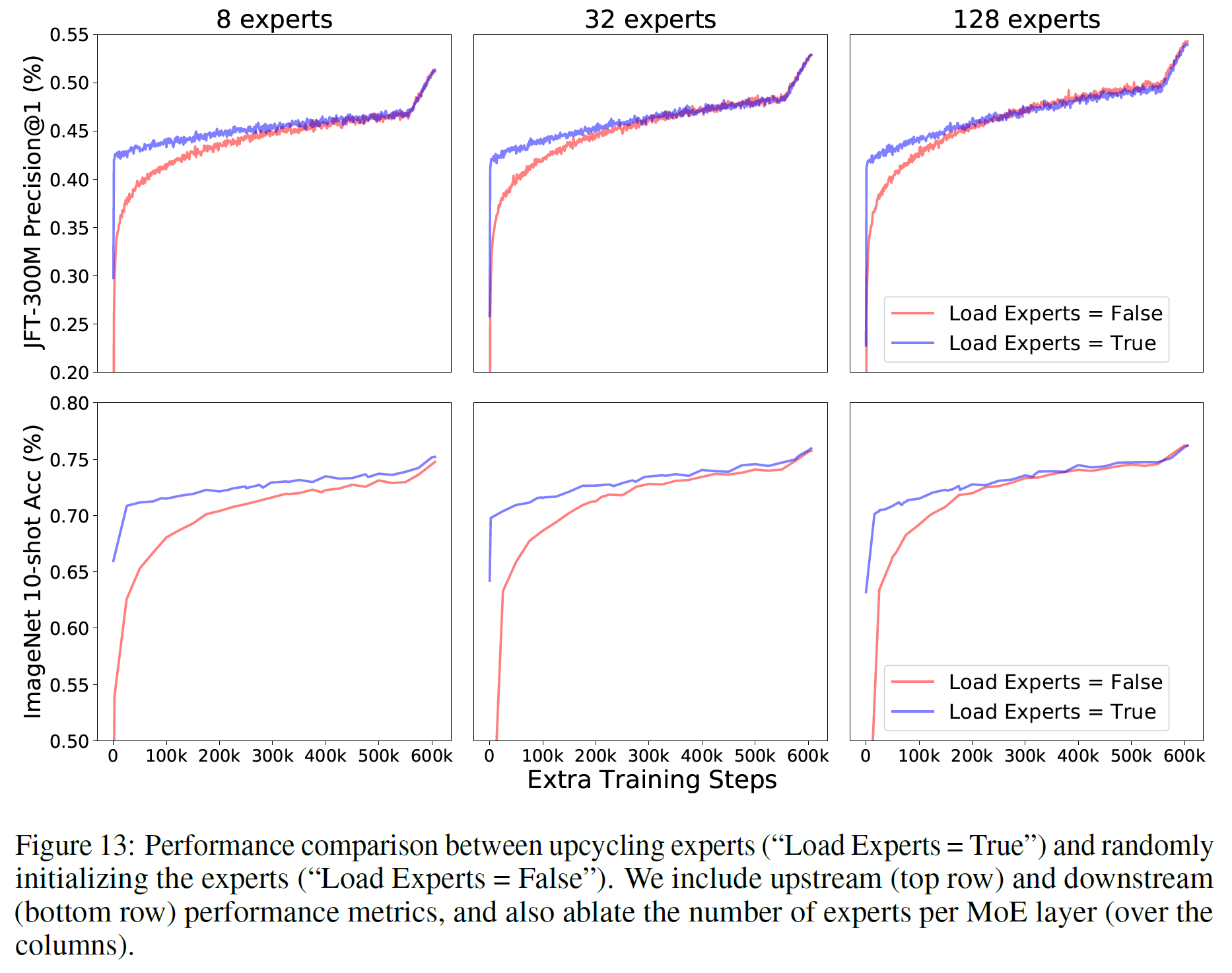
Number of Experts

• Adding more experts increases the model parameter count and quality
• Using very large number of expert shows large initial quality drop (Fig 10 left two)

5. Conclusion

• Provided Simple recipe to reuse pretrained dense checkpoints to initialize more powerful sparse models
• Smooth transition from dense to MoE
• Applicable for vision and language
• Upcycling of model

6. Comment

생각했던 것과는 다른 MoE였음. Expert를 선택하는 방법에 있어 Router을 이용할 수 있다는 아이디어와 Expert Choice라는 색다른 아이디어를 볼 수 있었음.