논문 정리 : Attention Is All You Need

Model Architecture

Attention

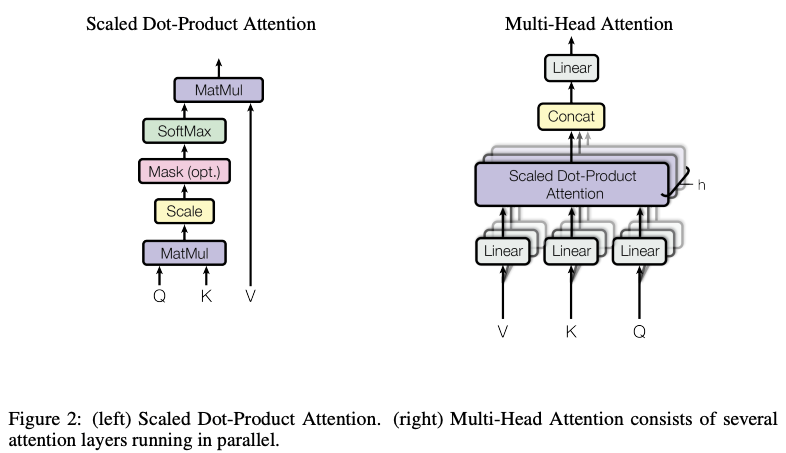
Scaled Dot-Product Attention

• Input : Query, Key, Value
• Process
  • $Attention(Q,K,V) = softmax(\frac{QK^{T}}{\sqrt{d_{k}}} )V$
    • $\frac{1}{\sqrt{d_{k}}}$ : scaling factor ($d_{k}$가 큰 경우, softmax function이 extremely small gradients로 만들 수 있기 때문에 제곱근)
    • Q, K, V : Matrix of packed Queries, Keys, Values
  • addictive attention
  • dot-product attention : much faster, space-efficient but highly optimized matrix multiplication code is needed

Multi-Head Attention

• allows the model to jointly attend to information from different representation subspaces at different positions
• implementation : 아래와 같이 설정하여 computational cost 비슷하게 만듦
  • $h=8$ (attention layers or heads)
  • $d_{k} = d_{v} = \frac{d_{model}}{h} = 64$

Applications of Attention in our Model

• multi-head attention 을 세 가지 방법으로 사용?
  • encoder-decoder attention layer
    • Queries from previous decoder layer
    • Keys, Values from output of encoder layer
    • 이유 : Decoder의 모든 위치에 있는 것들을 Encoder의 input sequence 전체에 대해 영향을 주기 위해(?)
  • encoder의 self-attention layer
    • Queries, Keys, Values from same place(previous encoder layer)
    • 이유 : Each position in the encoder can attend to all positions in the previous layer of the encoder.
  • decoder의 self-attention layer
    • Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot-product attention by masking out (setting to −∞) all values in the input
      of the softmax which correspond to illegal connections. See Figure 2.

Position-wise Feed-Forward Networks

• Encoder, Decoder layer에서 마지막에 FFN 있음
  • 각 위치에 대해서 separately, identically하게 동작(Layer 마다는 다른 인자이지만 같은 Layer안에서는 똑같은 Weight들로 모든 위치에서 동작함)
  • $FFN(x) = max(0, xW_{1}+b_{1})W_{2}+b_{2}$
  • Kernal size 1로 두번 convolution한다고 생각해도 됨(input, output의 dimensionality : 512, inner-layer dimensionality : 2048)

Embeddings and Softmax

• Learned embeddings 사용(다른 sequence transduction model 과 같이) : input token, output token을 $d_{model}$ 차원으로 vector화 하기 위해
• Learned linear transformation, softmax function 사용 : decoder output으로 next-token probabilities 계산 위해
• embedding layers, pre-softmax linear transformation에서 각각 같은 weight matrix 공유

Positional Encoding

• 단어의 임베딩 벡터에 위치 정보를 더하여 모델 입력으로 사용(위치 정보에 대해서 추가하기 위한 방법)
  • 이유 : 보통 convolution, recurrence 에서 위치에 대한 정보가 포함된 연산이 진행이 되지만 여기엔 없음..

$PE_{(pos,2i)}=sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})$
$PE_{(pos,2i+1)}=cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})$

• 위의 식이 2i, 2i+1 위치에 대해서 주변을 더 집중하게끔 하는 매커니즘이 있는걸 텐데..
  • 영어 문장 구조를 예시로 볼 때,
    • 3형식 : S V O
      • 홀수 번째에 대해서는 Cosine 인 이유가 바로 다음 단어인 V와의 관계 확인, 짝수 번째는 Sine 이면 V 보다는 O와의 관계를 더 보는 걸 것이고라는 대략적인 생각을 해보면 positional encoding으로 다양한 부분에 대한 관계를 확인하는 것이고, 그 결과로 나온 벡터 자체도 이러한 관계를 잘 표현한 것이라고 보면 될까;

Training

Training Data and Batching

English-German

• WMT 2014 English-German dataset 사용(4.5 million sentence pairs, 37000 tokens 로 target vocabulary)

English-French

• WMT 2014 English-French dataset (36M sentences with 32000 word-piece vocab)

Hardware and Schedule

• 8 NVIDIA P100 GPUS

Optimizer

• Adam optimizer with $\beta_{1}=0.9,\beta_{2}=0.98, \epsilon=10^{-9}$

Regularization

참조

• https://www.reddit.com/r/MachineLearning/comments/fbn0oe/d_attention_is_all_you_need_transformer_decoder/
• https://datascience.stackexchange.com/questions/51065/what-is-the-positional-encoding-in-the-transformer-model

d에 대해서 나누고 곱하는 이유에 대해

• Why does embedding vector multiplied by a constant in Transformer model? : https://stackoverflow.com/questions/56930821/why-does-embedding-vector-multiplied-by-a-constant-in-transformer-model
• https://stats.stackexchange.com/questions/534618/why-are-the-embeddings-of-tokens-multiplied-by-sqrt-d-note-not-divided-by-sq