[Algorithm] Basic sort

기본 정렬에 관한 정리

1) 선택정렬(selection sort)

포인트 :

• 정렬된 쪽과 정렬되지 않은 쪽 이렇게 두개로 나눠서 생각한다.

• 정렬되지 않은 리스트를 받았을 때, 첫 번 째 요소를 가지고(비교의 기준점) 그 외의 나머지 요소들과 비교한다.

• 나머지 요소들 중에 비교의 기준점이 되는 요소보다 작은 값이 있다면, 둘의 위치를 바꾼다.

• 이렇게 첫 번 째 시행을 하면, 인덱스를 기준으로 인덱스 0은 정렬된 부분이고 1~n은 정렬되지 않은 부분으로 나뉜다.

• 비교의 기준점이 되는 인덱스를 +1해서(아까는 0이었다면 이제 1로가서), 위의 과정을 반복한다. 즉, 인덱스 1의 요소와(비교의 기준점) 2~n의 요소를 비교하여 기준점보다 작은 값이 있다면 둘을 교환하고, 없으면 그대로 둔다.

• 이 과정이 끝나면 똑같이 0,1 까지는 정렬이 된 상태이고, 2~n은 정렬되지 않은 상태가 된다(두개로 나눠진다).

• 이 과정을 반복하며 끝 요소까지 시행하면 오름차순 정렬이 된다.

​

구현상의 포인트

• 선택 정렬의 포인트는 최솟값과 현재 기준점이 되는 요소의 '교환'이다.

• 이 '교환' 과정을 위한 방법으로는 index가 메인 포인트가 된다.

• 즉, 기준점이 되는 요소와 교환할, 달리 말해, 기준점이 되는 요소보다 작은 값을 찾으면 indx 변수에 해당 인덱스를 넣으면서 탐색한다.

• 끝까지 탐색했을 때, indx 변수에 들어있는 인덱스가 가장 작은 값의 인덱스가 되고, 이 인덱스에 위치해있는 값과 기준점이 되는 값을 교환하는 식으로 한번의 시행이 완성된다.

​

실제 구현

백준에 있는 기본 정렬문제를 파이썬 코드로, 그리고 선택정렬로 풀어봤다.

위와 같이

주어진 리스트를 인덱스 0부터 하나하나 탐색을 기본으로 하되(위에 용어로 표현하면 기준점이 되는 요소를 하나하나 탐색해 나간다),

2중 for문으로 그 아래는 기준점이 되는 요소의 바로 다음 인덱스 요소부터 리스트를 끝까지 탐색하는 시행을 한다.

이 시행을 하면서 기준점이 되는 요소보다 작은 요소를 찾았을 경우 min이라는 변수에 해당 인덱스를 넣어준다.

이 때, 시행을 끝까지 함에 따라 min은 몇번이고 바뀔 수 있다.

이렇게 기준점이 되는 요소 1개와 그 나머지 요소를 가지고 탐색을 마쳤을 경우(2depth for문이 끝난 경우)

마지막에 min에 있는 인덱스가 최소값의 인덱스일테니

기준점이 되는 요소와 min 에 있는 요소를 바꿔준다.

그런 다음 min은 다시 기준점이 되는 요소의 인덱스로 리셋해주고, 위와 같은 시행을 반복해준다.

그렇게 리스트의 모든 요소를 탐색(끝에서 두번째까지만 해줘도 됨)하면, 원하는 오름차순 정렬이 된다.

​

같은 로직을 자바스크립트로 구현

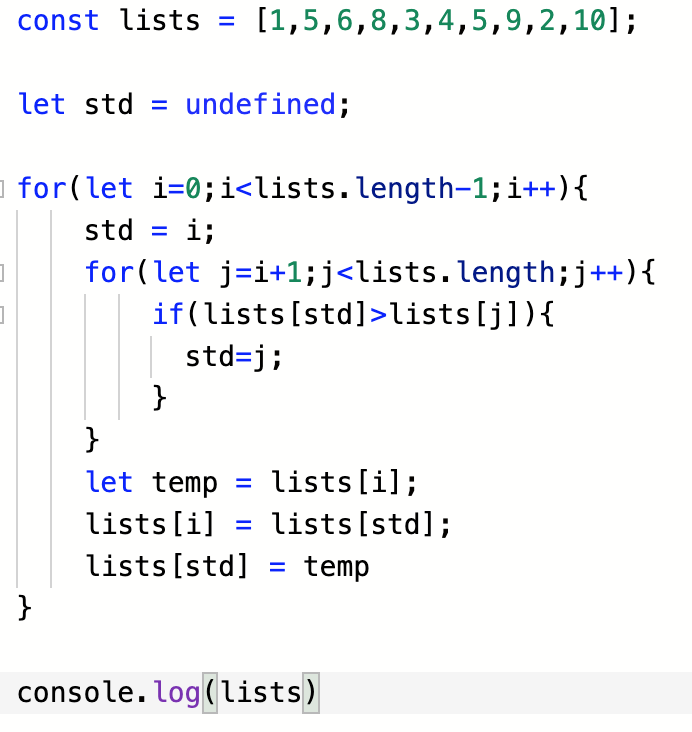
이 때, 내림차순 정렬은

이 부분의 부등호만 반대로 해주면 된다.

즉, 기준점이 되는 요소와 그 나머지 요소를 비교하면서 탐색하되

나머지 요소 중에 기준점이 되는 요소보다 큰 요소가 있다면, 그 요소의 인덱스 값을, 이 경우에는 max라는 변수에

넣어주면서 탐색하면 된다.

그리고 똑같이 기준점이 되는 요소와 최대값이 되는 요소를 변경해주면서 내림차순 정렬을 완성시켜가면 된다.

​

마무리

: 선택정렬은 기본적으로, 리스트의 모든 요소(끝에 하나를 빼더라도 일단 n-1개니까 n개)를 탐색하면서

그 요소 하나하나를 기준점으로 삼으면서(첫 번 째 for문)

그 기준점이 되는 요소 이외의 리스트 요소와 하나하나 비교하면서 최소값을 찾아 위치를 교환하는 방식이기 때문에(2중 for문)

O(n**2)의 시간 복잡도를 가진다.

​

​

2) 삽입 정렬(insertion sort)

포인트 :

• 정렬된 쪽과 정렬되지 않은 쪽을 먼저 나눠서 생각한다.

• 앞부분을 정렬된쪽, 뒷부분을 정렬되지 않은쪽이라고 생각한다.

• 핵심은 리스트를 탐색하면서 앞부분에 탐색 중인 요소를 정렬된 순서에 알맞게 '삽입'하는 것이다.

• 리스트가 있을 때, 인덱스 1부터 탐색하면 된다. 맨 첫 번 째 요소는 이미 맨 앞에 있으므로 더이상 비교할 것이 없다.

• 예를 들어, [4,1,3,5] 가 있을 때, 먼저, 1을 기준으로 4와 비교해서 4>1이므로 4와 1의 위치를 바꿔준다(정렬된 순서에 알맞게 삽입).

• 다음으로 인덱스 2로가서, 3을 기준으로 [1,4,3,5]인 상태에서 먼저 4와 비교하고, 4>3 이므로 [1,3,4,5] 로 둘의 위치를 바꿔준다.

• 다음으로 1과 3을 비교했을 때 1<3 이므로, 더이상 비교할 필요가 없이 시행을 끝낸다.

• 그러면 현재 [1,3,4,5]가 되고, 마지막으로 인덱스 3으로 가서 시행을 하면 끝이난다.

• 포인트는 이름 그대로 '삽입'의 개념이지만, 하나하나 비교하면서 옮기면서 삽입하는 것이라고 생각하면 될 것 같다.

• 그리고 '하나하나 비교하기 위해' 현재 인덱스의 요소와 바로 앞의 인덱스의 요소를 비교하는 것을 반복하며 앞부분으로 나아간다.

​

구현상의 포인트 :

• 선택 정렬과는 달리 인덱스를 변수에 담아가며 할 필요가 없다.

• 현재 인덱스의 요소와 바로 앞 인덱스의 요소 이렇게 두개만을 비교하면서 현재 인덱스 요소 앞의 모든 요소를 탐색하면 된다.

• 그렇게 탐색하다가 앞의 요소가 더 크면 둘의 위치를 바꿔주고, 앞의 요소가 더 작으면 원하는 대로 오름차순 정렬이 된 것이므로 해당 인덱스와 관련된 시행은 끝내고, 다음 인덱스로 넘어가서 같은 시행을 반복한다.

• 그렇게 리스트의 요소 끝까지 이 시행을 반복하면 정렬이 완성된다

​

실제 구현

​

• 파이썬 :
  

코멘트 : 선택 정렬이 리스트의 맨앞의 요소를 차례대로 그 뒷요소들과 비교하여 각 시행마다 최소값을 앞 부분에 위치시키는 방식으로 정렬을 해나아가는 것이라면, 삽입 정렬은 리스트의 두번째 요소부터 시작해서 그 앞요소들 하나하나와 비교해나가면서 순서를 재배치하고, 그 다음 요소도 같은 방식으로 재배치해 나아가는 방식인 것 같다.

​

• js
  

​

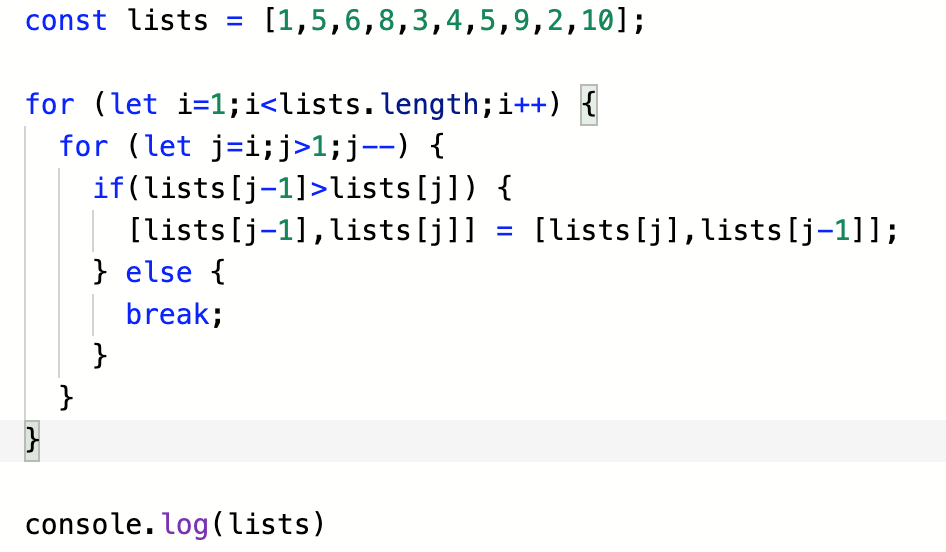
코멘트 :

굳이 선택 정렬과 삽입 정렬을 비교했을 때, 선택 정렬은 2depth 탐색을 할 때, 끝까지 탐색을 해야만 한다. 기준이 되는 값보다 작은 값이 있는지 알기 위해서는 끝까지 탐색을 해봐야알기 때문에!. 그러나, 삽입 정렬은 기준이 되는 값보다 작은 값을 찾는 다는 점에서는 비슷하지만, 탐색하는 부분이 이미 정렬이 되어있기 때문에(선택 정렬은 탐색하는 부분이 정렬된 부분이 아님), 기준값보다 작은 값을 찾으면 그 즉시 탐색을 종료하고, 다음 요소로 넘어간다. 따라서, 둘다 O(n2)의 시간 복잡도를 가지지만, 최선의 케이스를 생각해봤을 때, 삽입정렬은 만약, 리스트가 이미 정렬된 상태라면, O(n)의 시간복잡도를 가지고, 선택정렬은 이미 정렬된 리스트라 하더라도 똑같이 O(n2)의 시간복잡도로 연산을 하게 된다. 무조건 비교 시행을 하기 때문!(삽입 정렬처럼 더이상 비교할 필요가 없는 상황이 없음)

​

3) 버블 정렬(bubble sort)

​

포인트 :

• 정말 거품(버블)이 나는 것처럼 정렬할 때 일사분란(?)하게 움직이는 형태의 정렬 방법이다..

• 포인트는 시작 요소부터 탐색하며, 바로 다음요소와 크기를 비교후에 만약 앞의 요소가 더 크면 둘의 위치를 바꾼다.

• 그 다음에 다시 다음 인덱스로 가서 앞선 방법처럼 둘을 비교후 위치를 바꾸거나, 바꾸지 않는다.

• 그런식으로 한번을 쭉 탐색하면 결국 마지막 인덱스에 해당 리스트에서 가장 큰 수가 위치하게 된다(앞에서부터 끌어모아서? 가장 큰수를 계속 찾아가며 맨 뒤까지 이동시켰으므로)

• 한번의 리스트 탐색 후에, 다시 똑같이 첫요소부터 같은 방법의 시행을 계속한다. 이 때, 맨 끝에는 이미 가장 큰수가 온 것이 확실하므로,

이전 시행에서 채워진 끝에서부터 n번째 수는 탐색하지 않아도, 즉, 비교하지 않아도 된다.

• 이런식으로 리스트 요소의 개수번만큼 탐색을 하면(계속 가장 큰 수를 뒤로 보내는 식으로), 오름차순 정렬을 할 수 있다.

• 선택 정렬과 같이 가장 이상적인 케이스, 즉, 이미 정렬된 리스트가 제시되어도 O(n**2)의 시간 복잡도를 지님

​

구현 포인트

• 한번씩 리스트를 전체 탐색한 뒤에 다음 시행 때 이미 맨 뒤에 정렬된 최대값은 제외하고 탐색을 하도록 구현해야하는 것이 포인트

​

실제 구현

​

• js
  

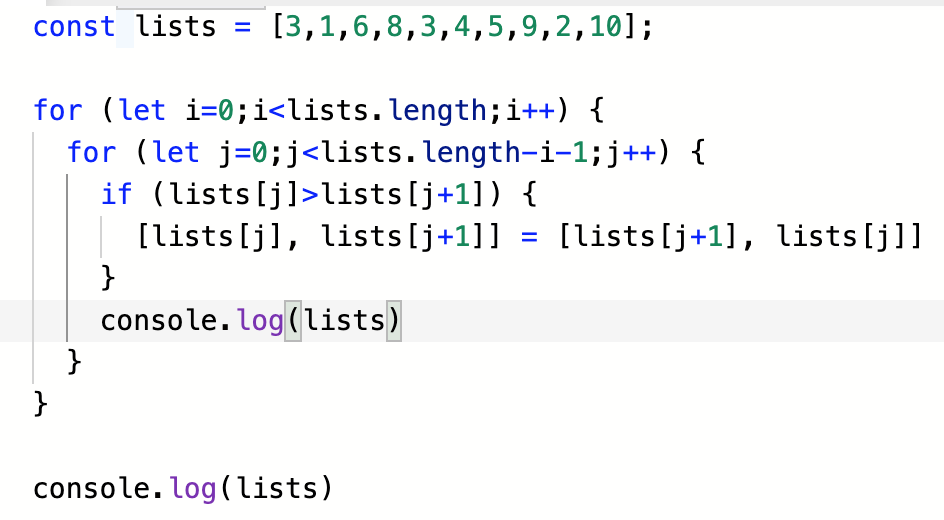
이 코드 중간에 lists가 어떤식으로 변화해가는지를 출력해보면

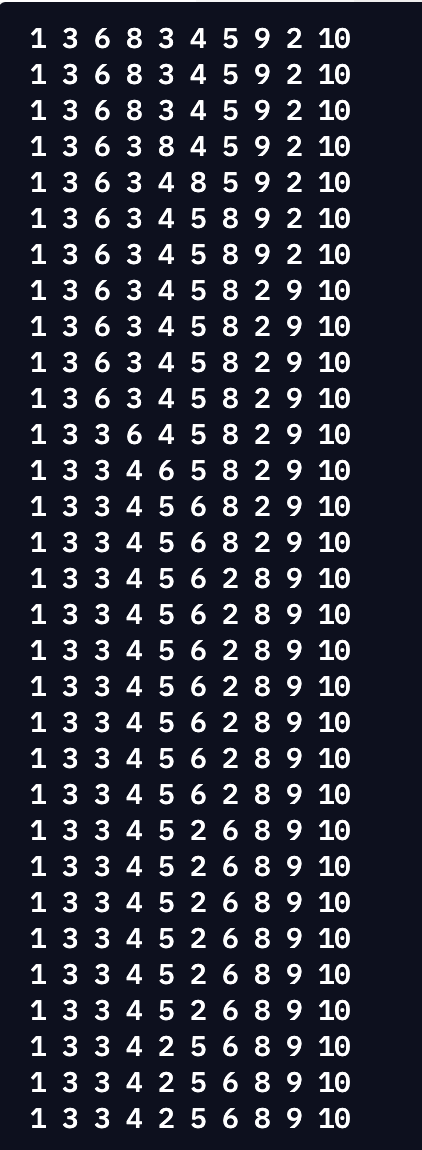
이런식으로 시행마다 큰수를 점점 뒤로 미는 것을 볼 수 있음(이미 제대로 정렬이 되어있다면 변화가 없는 부분도 있음)

버블 정렬의 포인트는 비교 후에 큰 수를 맨뒤로 보내면서, 첫 번 째로 큰 것, 두 번 째로 큰 것 이렇게 순서대로 뒷부분을 채우며

정렬을 하는 방식에 있는 것 같다.

​

• 파이썬
  

마무리 :

셋 중에 뭐를 써야할지에 대해서는 각각의 장단점에 대해서 좀 더 공부해본 뒤에야 말할 수 있을 것 같다.

복습할 때 각각의 장단점에 대해서 다시 포스팅을 올려야겠다