용어 정리

• Loss Function : f(x)의 Loss가 얼마인지 계산하는 함수
• Optimizer : 최적화(Optimization)을 수행하는 알고리즘 ex. SGD, Adam
• One-hot Class Vector : 각 클래스에 대한 확률을 표현한 벡터 ex. <0, 0, 0, 1, 0>
• Ground Truth : 기계학습에서는 데이터 원본 혹은 실제 값을 의미함

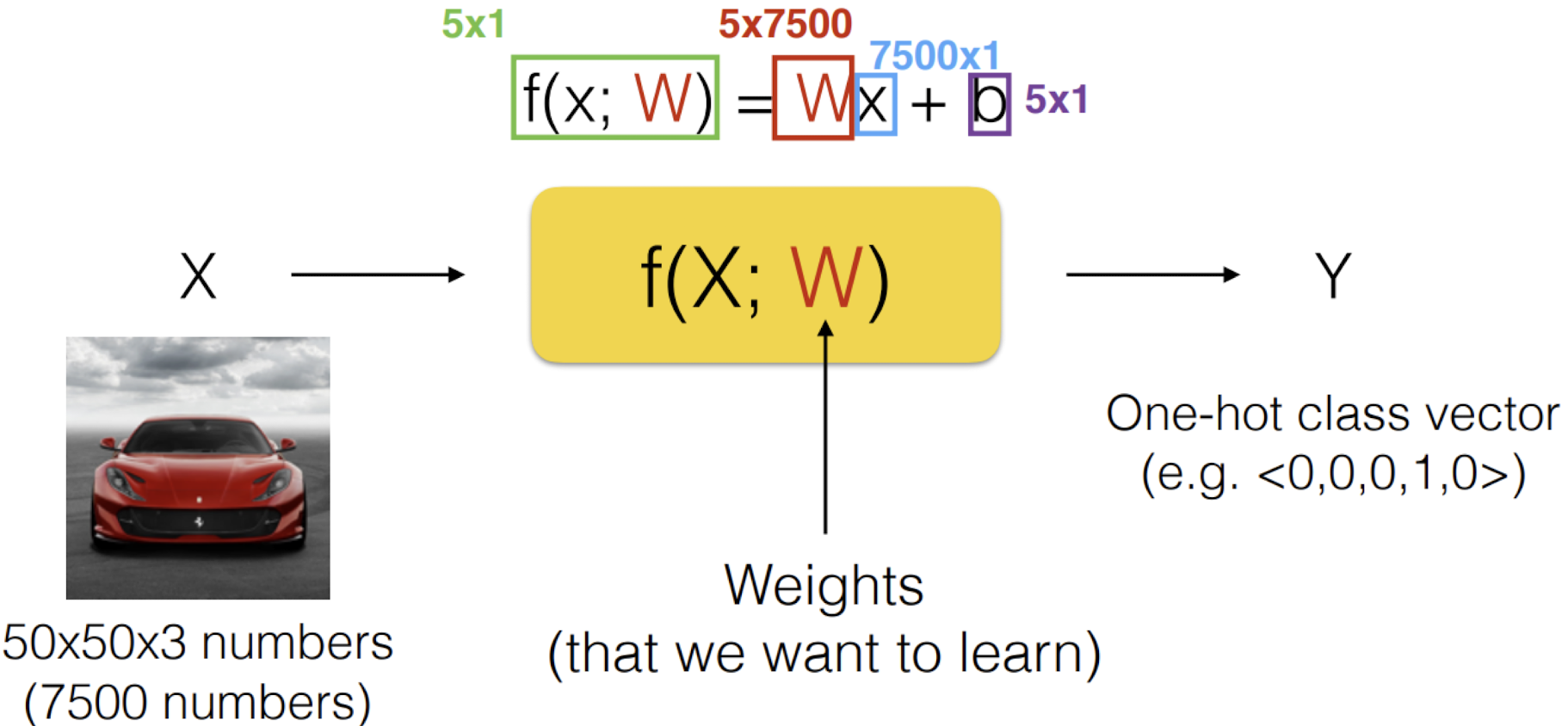
Linear Classification

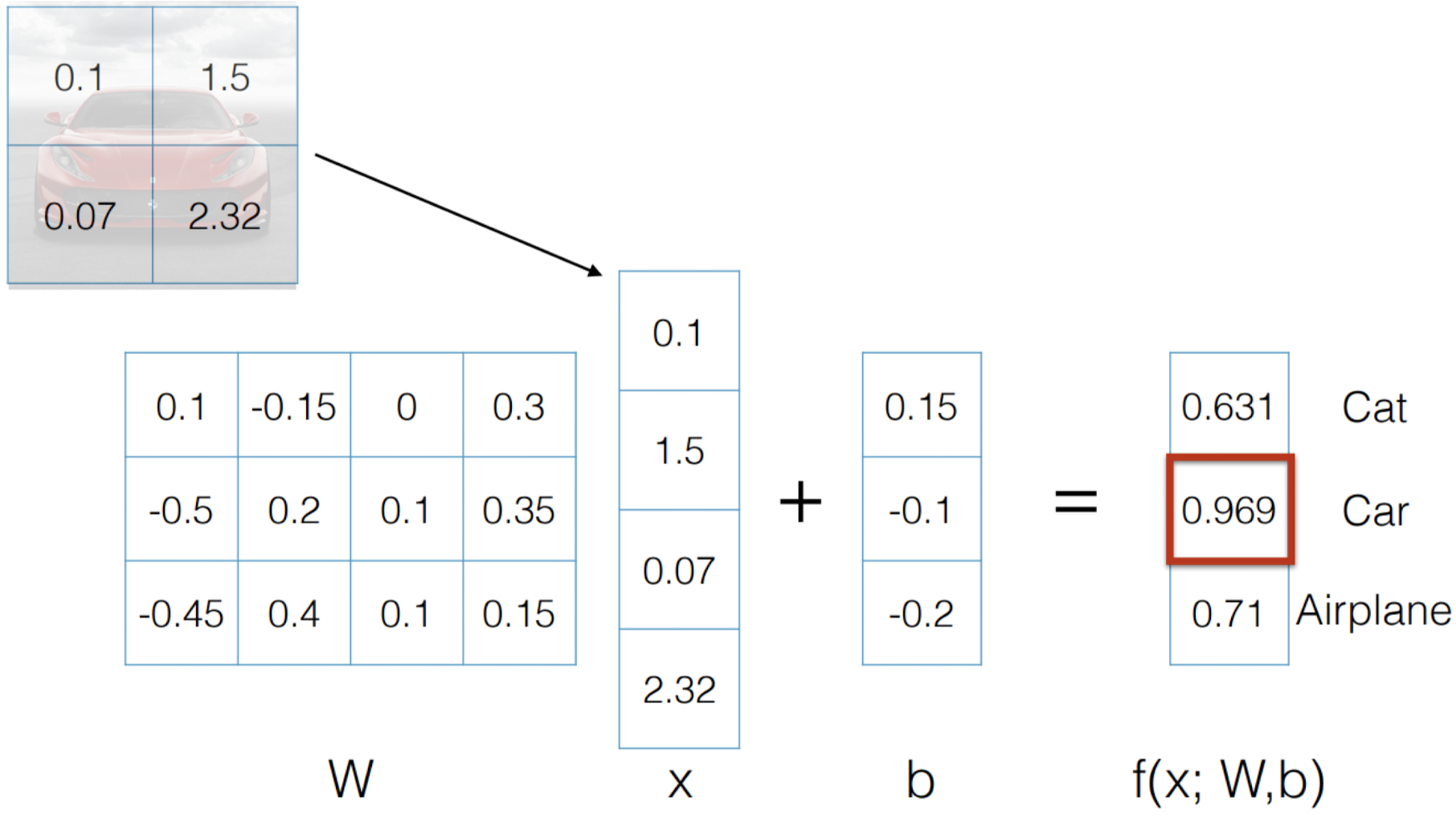
f(W, b) = Wx + b

위의 예시에서 각 요소의 행렬의 크기를 알아보자.

f(W, b) : 3 (클래스의 개수)
W : 12 (클래스의 개수 * 데이터의 개수)
x : 4 (데이터의 개수)
b : 3 (클래스의 개수)

Loss Function

L1 Loss

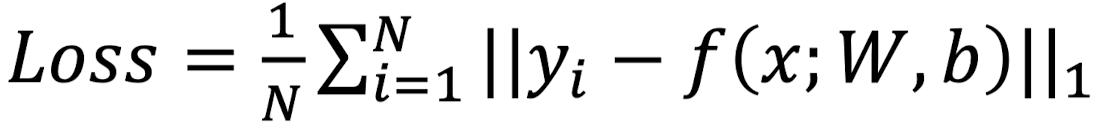
L2 Loss

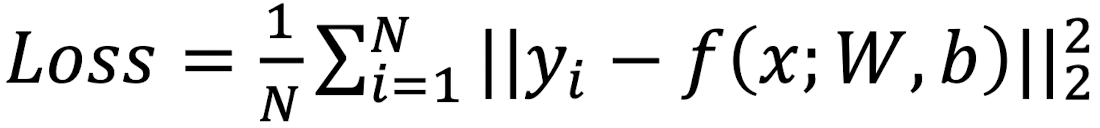
L2 Loss는 MSE(Mean Squared Error, 평균 제곱 오차)라고도 부른다.

Cross Entrophy Loss

Cross Entrophy Loss는 L1, L2 Loss와는 달리, 확률끼리 비교하는 것이다.

Cross Entrophy Loss에서 Loss를 계산하는 식은 다음과 같다.

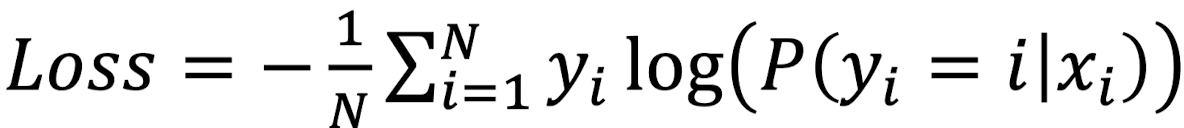
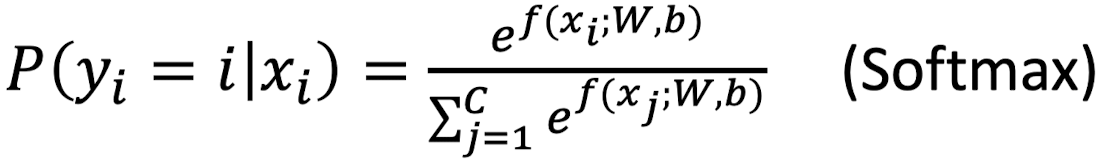
다음은 Loss Function별로 Loss 값을 나타낸 그래프이다.

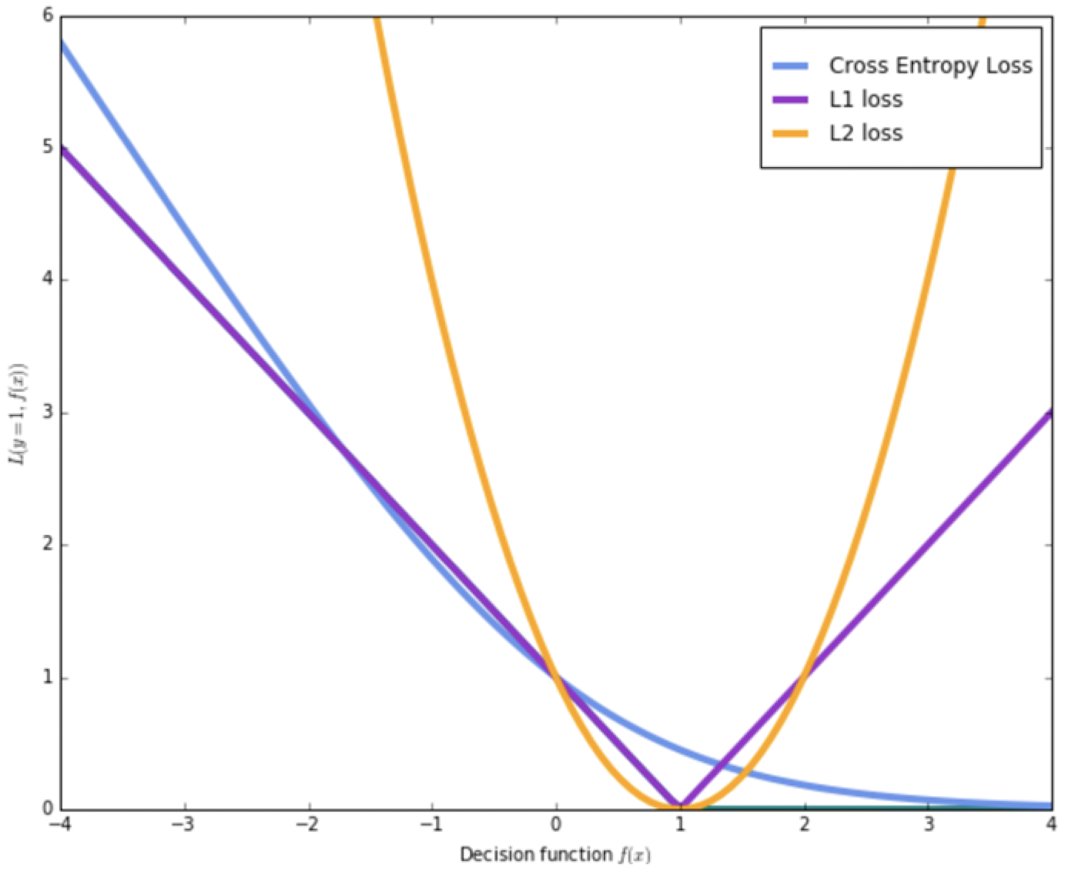
같은 W, b를 사용하더라도 어떤 Loss Function을 사용하는지에 따라 결과가 달리진다.

Regularization (정규화)

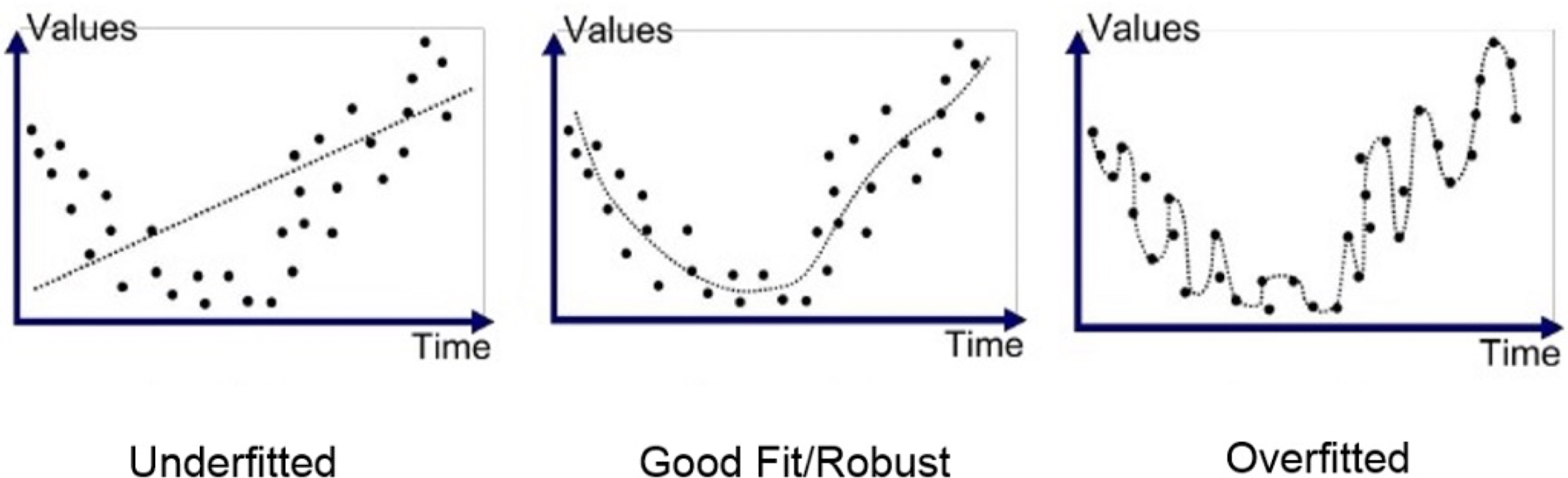
Underfitted는 모델의 복잡도가 너무 낮아서 데이터를 잘 판별하지 못하는 경우를 말한다.

이와 반대로, Overfitted는 모델의 복잡도가 너무 높아서 예측 능력이 망가지는 경우이다.
이 경우 학습 데이터에 대해서는 error가 적지만, 모델이 예측하는 데이터의 전체적인 경향성이 망가지기 때문에 새로운 데이터가 들어왔을 때의 예측력이 낮아진다.

cf. 모델의 복잡도가 높다는 건 학습할 파라미터가 많다는 말이다.

Ockham's Razor

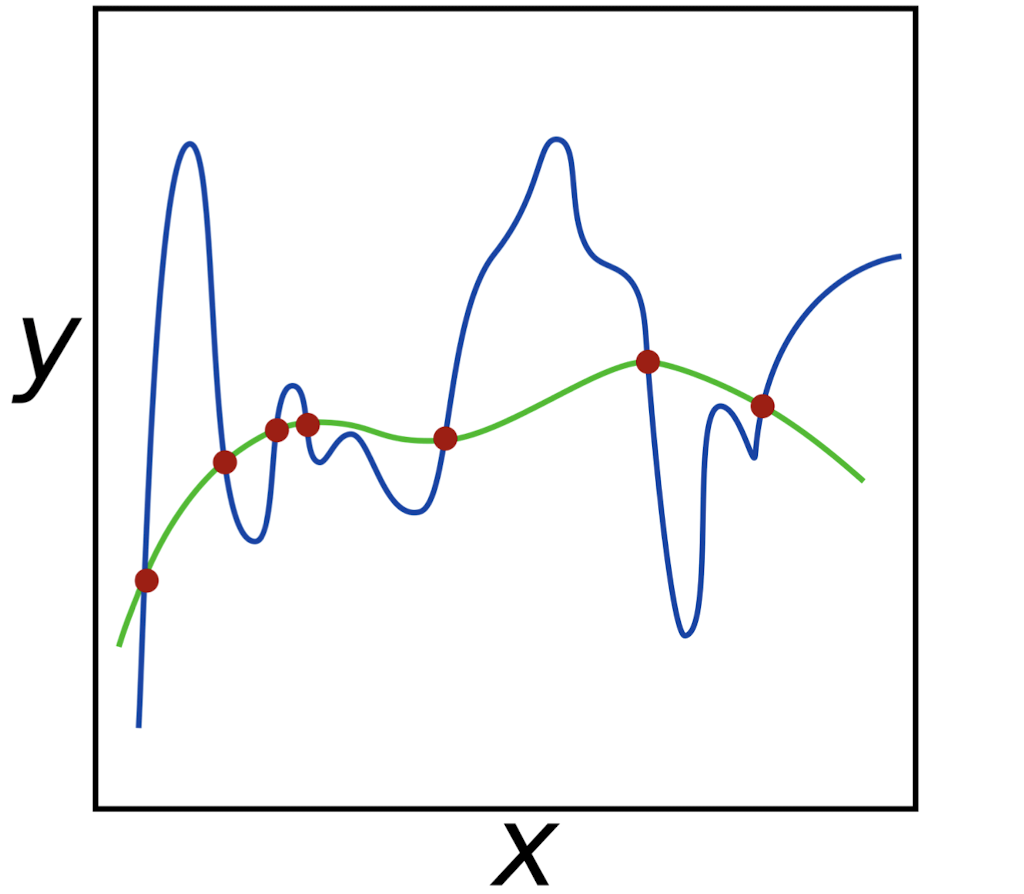
Ockham's Razor(오캄의 면도날 법칙)은 경쟁하는 여러가지 가설 중에 가장 간단한 것이 가장 좋은 것이라는 법칙이다. 위의 그래프의 경우 초록색 그래프가 더 좋다는 말로,
Overfitted 모델보다 Good Fit / Robust 모델이 더 좋다는 말에 힘을 실어준다.

Regularization (정규화)

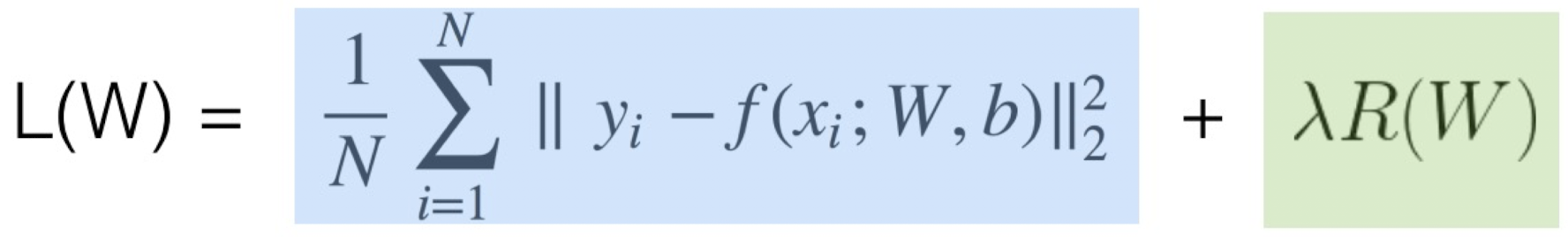
위 식의 파란색 부분은 Data Loss를 구하는 부분으로, 이 Loss를 최소화함으로써 학습 데이터에 fitting하는 과정이다. 이 과정을 Optimization(최적화)라고 부른다. 하지만, Overfitting의 경우 예측력이 떨어진다는 것을 알게 되었다. 따라서 초록색 부분인 Regularization(정규화)를 통해서 Simple Model로 만들어주는 과정이 필요하다.

Optimization을 하는 방법으로 총 3가지가 있다.

1. Ramdom Search
   -> 시간이 너무 오래 걸린다.

2. Analytic Solution(방정식 풀기)
   -> 차수가 높아지면 방정식을 푸는 것이 거의 불가능하다.

3. Numerical Solution(Gradient Descent)
   -> Local Minima에 갇힐 수 있고, 미분값이 수렴하지 않고 발산할 수 있다

각각의 방법들에는 이러한 문제점들이 있다.
이에 대한 해결책으로 등장한 것이 Neural Networks(인공신경망)이다.

Neural Networks (인공신경망)

Neural Network란?

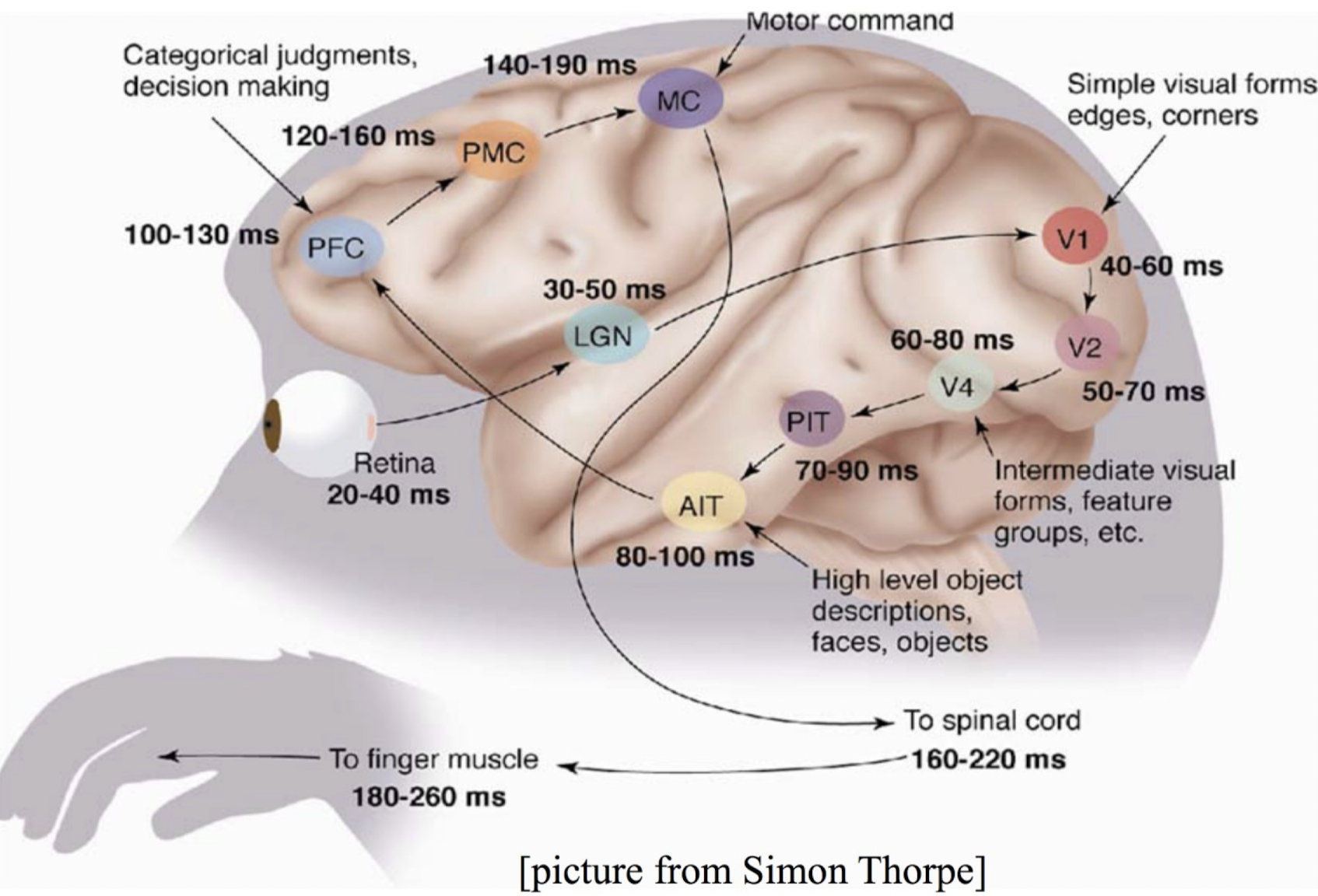
딥러닝은 인간의 뇌 구조에서 착안한 기계학습 방법이다.
인간의 뇌는 위의 그림과 같은 복잡한 연쇄를 통해 Output을 도출한다.

Neural Network란 뉴런(Atomic Functions)이 Non-linear하게 연결되어 있는 구조를 말한다.

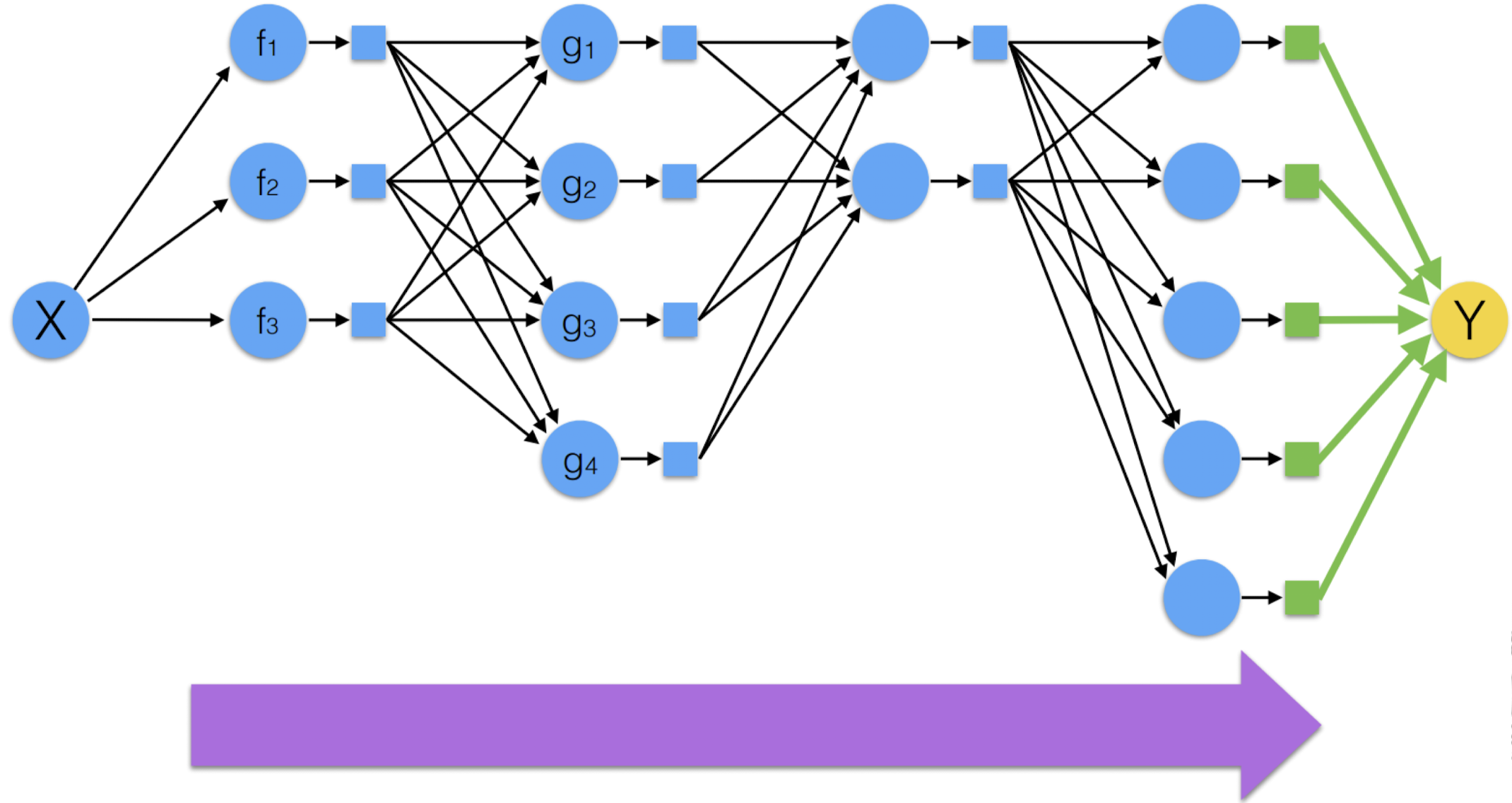
위의 그림은 Neural Network가 Forward Propagation(순전파)을 통해 Output을 찾아가는 과정을 보여준다.

그렇다면, 각각의 Atomic Functions를 어떻게 알 수 있을까?
이를테면 각 Atomic Functions의 W(Weight) 말이다.
바로 Backward Propagation(역전파)를 통해 계산할 수 있다.

Back Propagation (역전파)

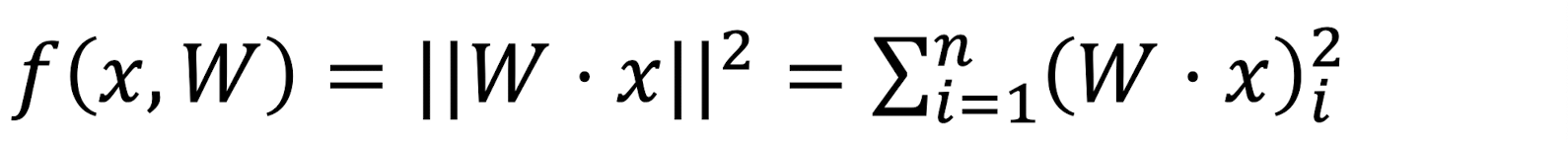
위의 f(x, W)에 대한 역전파 과정을 살펴보자.

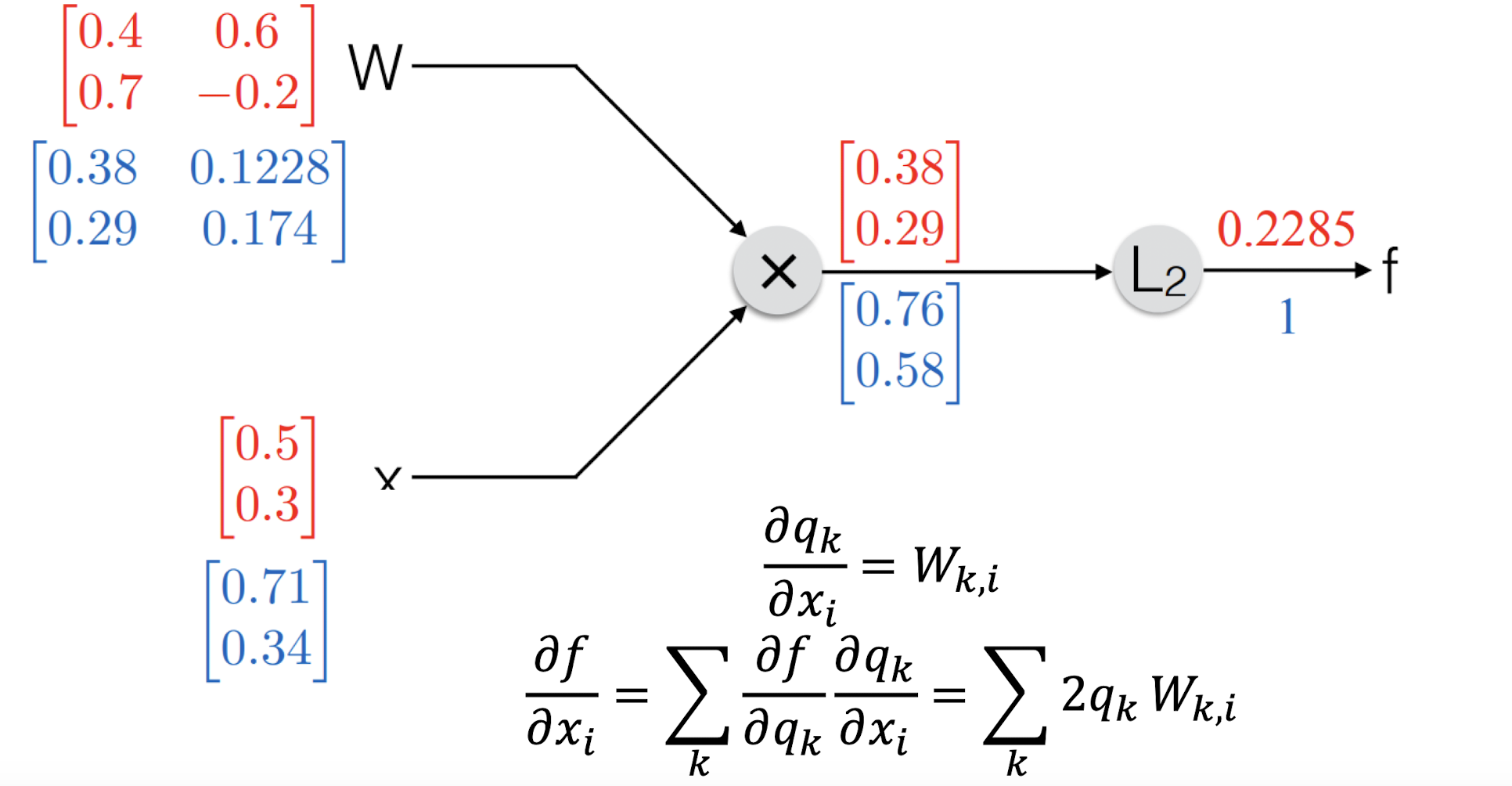
Chain Rule을 통해 f에서 역행하는 방향으로 이동하면서 미분값을 구할 수 있다.

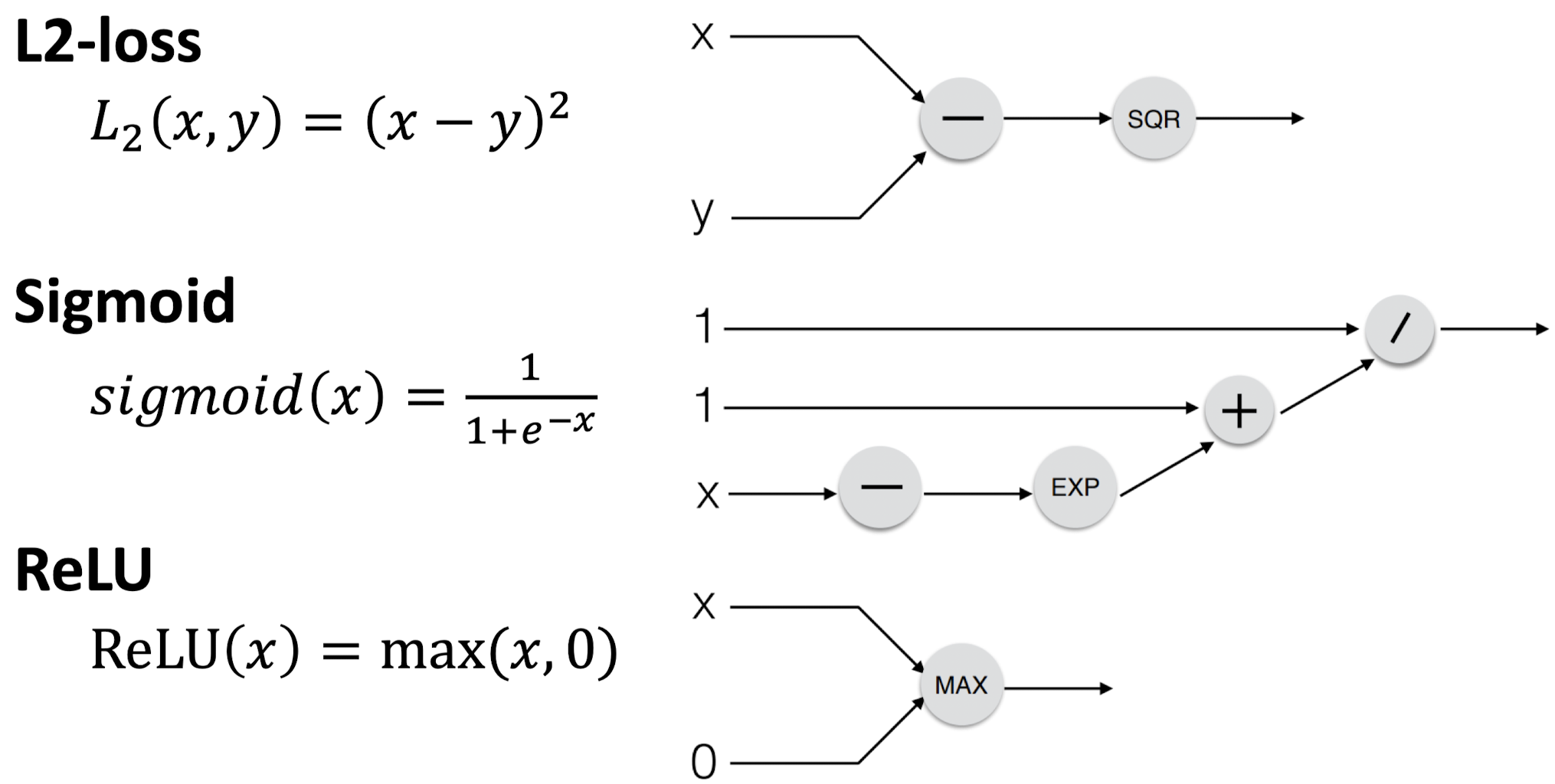
다음으로는 Loss Function인 L2-Loss와 Activation Function(활성화 함수)인 Sigmoid와 ReLU의 Computational Graph를 살펴보자.

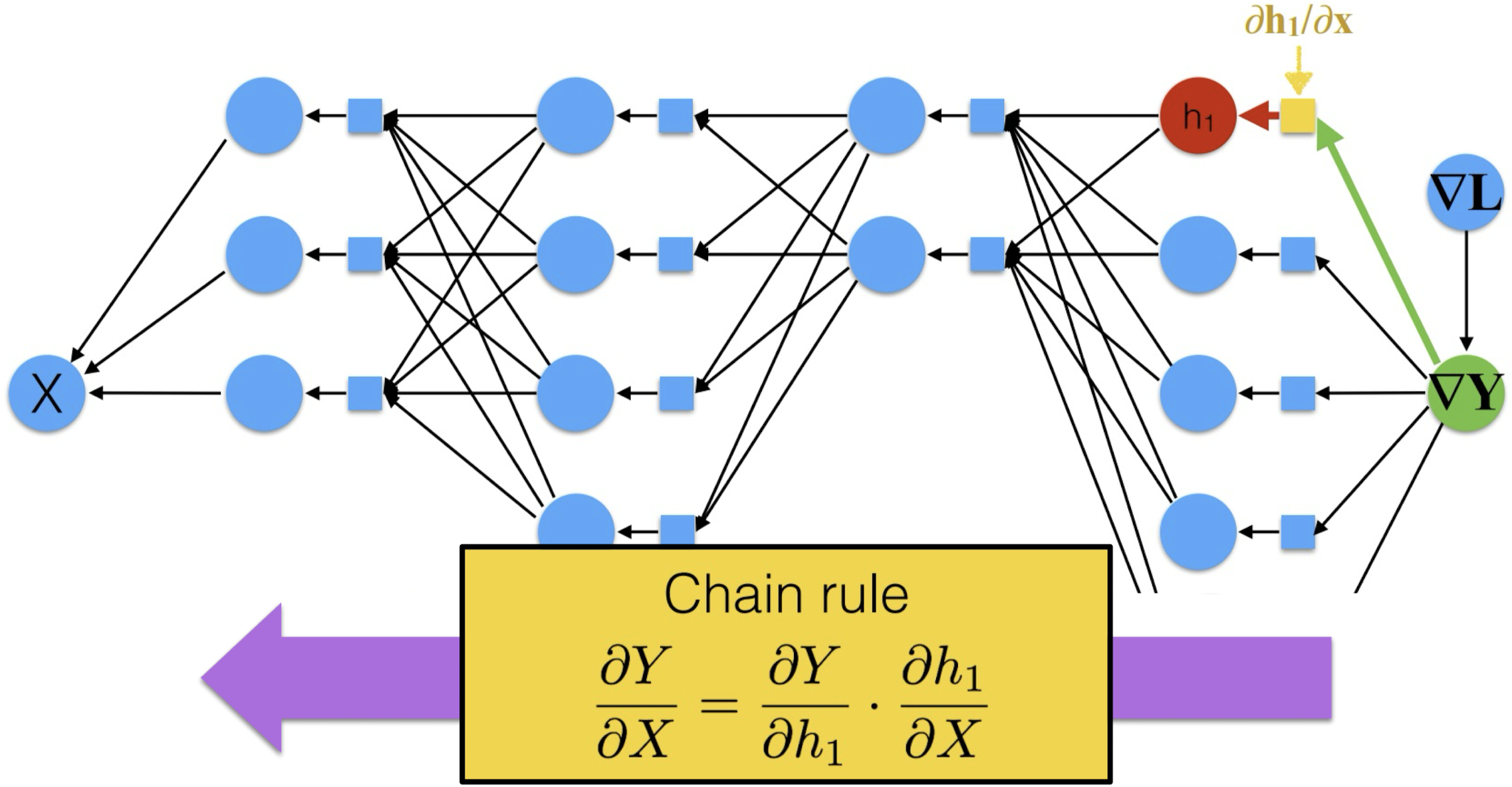
이런식으로 Chain Rule을 통해 Y에서 X로 가면서 미분값을 구하는 것이 Back Propagation이다.