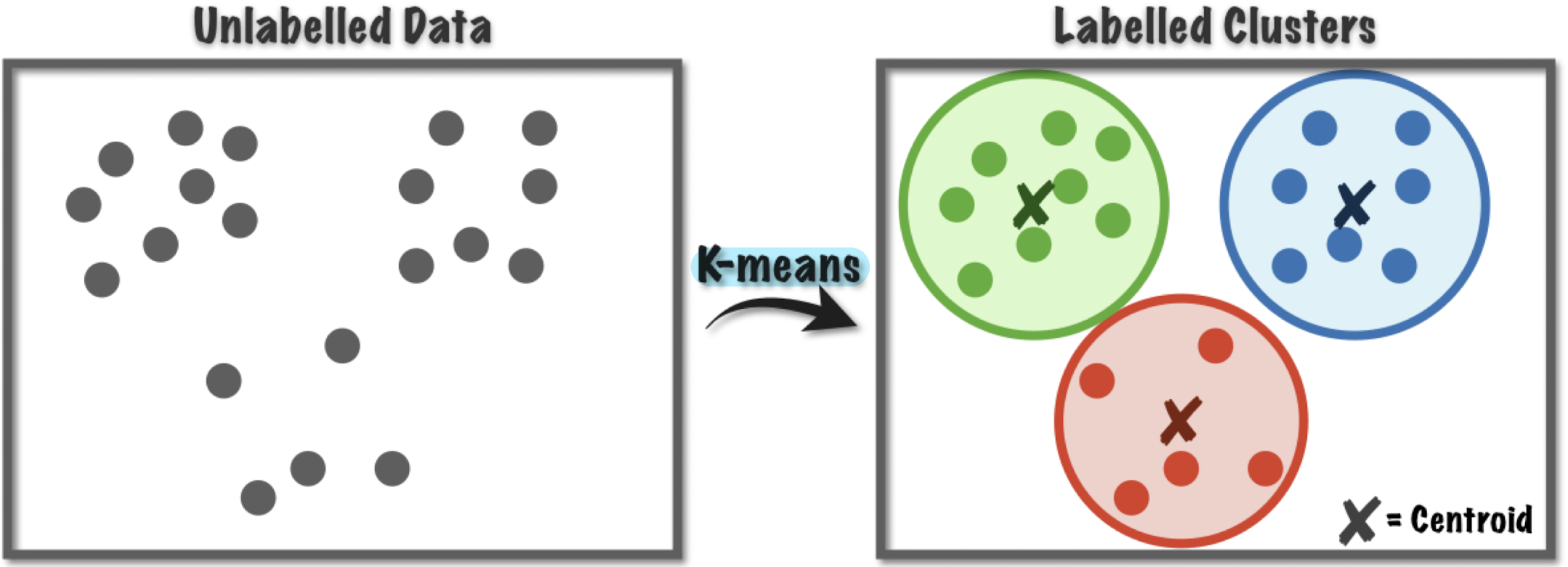
Traditional Unsupervised Learning (전통적 비지도학습)
K-means
K-means란?
K-means는 비지도학습 방법 중 하나로, Clustering(군집화) Method이다.
비지도학습은 지도학습과는 달리 정답이 주어지지 않기 때문에 Classification을 하지는 못하고, clustering을 할 수밖에 없다.
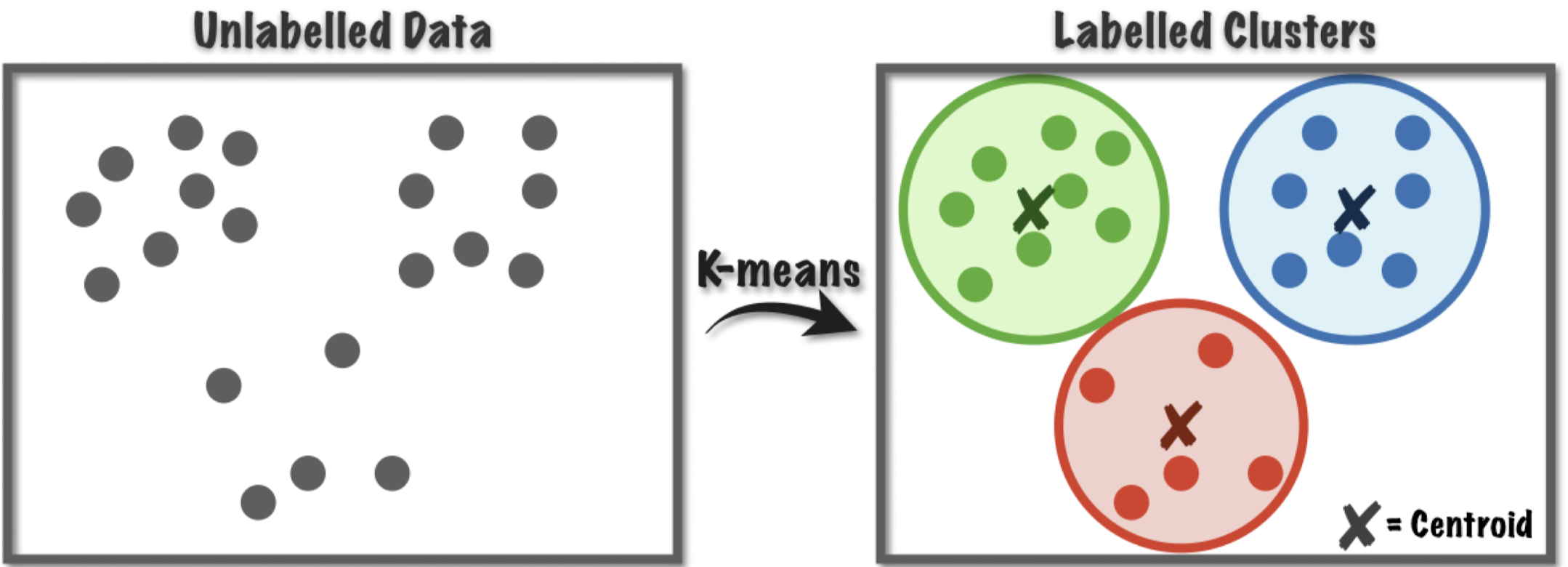
K-means는 주어진 n개의 데이터를 K개의 Cluster로 나눈다.
이때 각 cluster의 중앙값을 Centroid라고 한다.
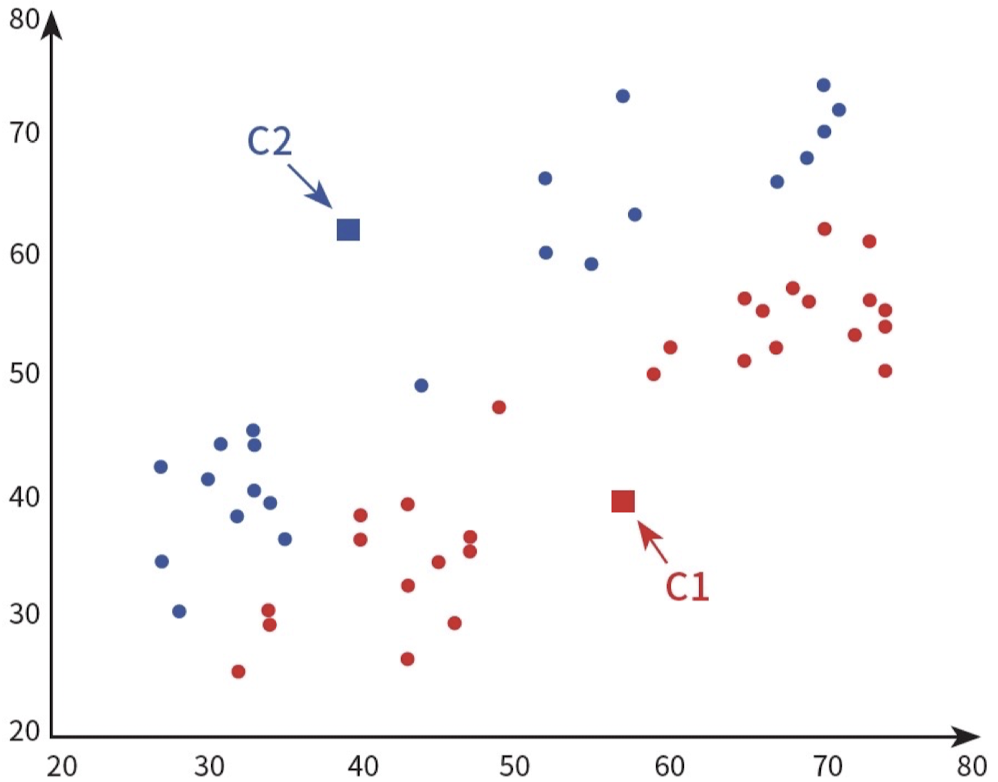
K-means에서는 첫 시행에 랜덤으로 Centroid를 K개 정하고, 모든 점에 대해 어떤 Centroid에 가장 가까운지 계산해서 해당 Centroid의 Cluster로 편입한다.
위 그림은 K가 2인 경우 K-means의 첫번째 실행이다.
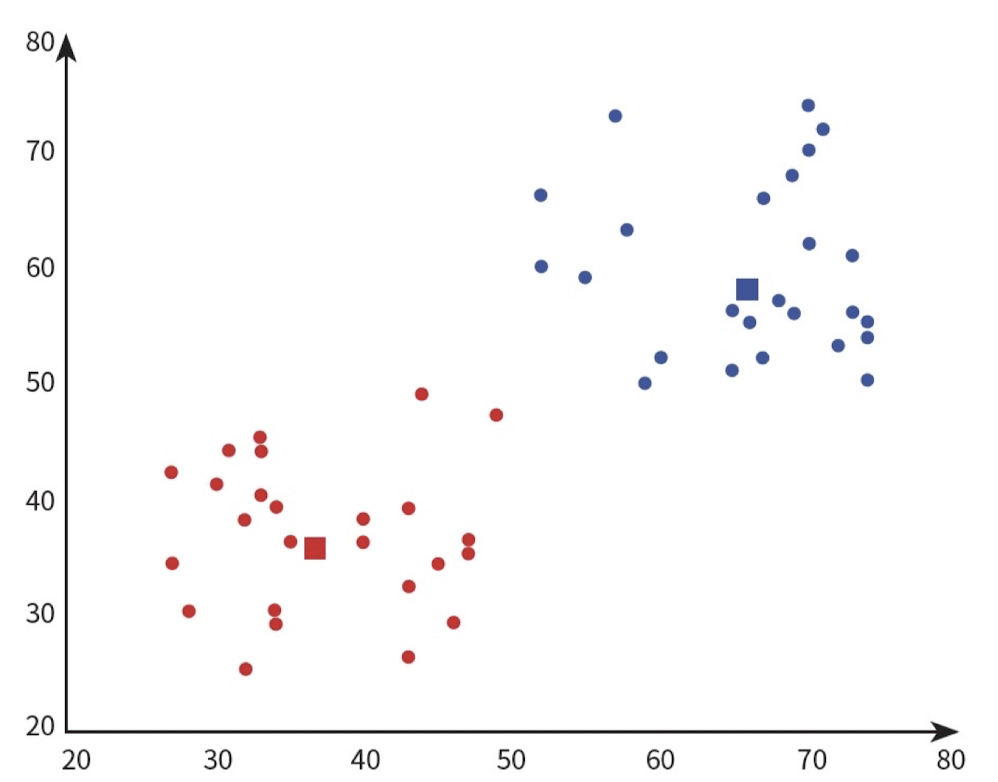
이후 각 Cluster의 중앙값을 새로운 Centroid로 정하고, 더 이상 Centroid가 바뀌지 않을 때까지 같은 과정을 계속 반복한다. 첫번째 실행에서 Centroid와 Cluster 결과 모두 다른 것을 확인할 수 있다.
K를 어떻게 결정할까?
K-means에서 K는 Hyper Parameter이다. 따라서 우리가 튜닝해야 되는 대상이다.
하지만, Clustering Method에는 label이 없기 때문에 Cross Validation을 사용할 수 없다. 그렇다면 어떻게 K를 결정할 수 있을까?
다음은 K를 1씩 증가하면서 각각의 SSE(Sum of Squared Errors)를 계산하는 코드이다.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
X = np.array([
[6,3], [11,15], [17,12], [24,10], [20,25], [22,30],
[85,70], [71,81], [60,79], [56,52], [81,91], [80,81]])
plt.scatter(X[:,0],X[:,1])
n_clusters = range(1, 10)
kmeans = [KMeans(n_clusters=i) for i in n_clusters]
# For every sample, the squared error is calculated and added to the list.
score = [kmeans[i].fit(X).inertia_ for i in range(len(kmeans))]
plt.plot(n_clusters, score)
plt.xlabel('Number of Clusters')
plt.ylabel('Score')
plt.title('Elbow Curve')
plt.show()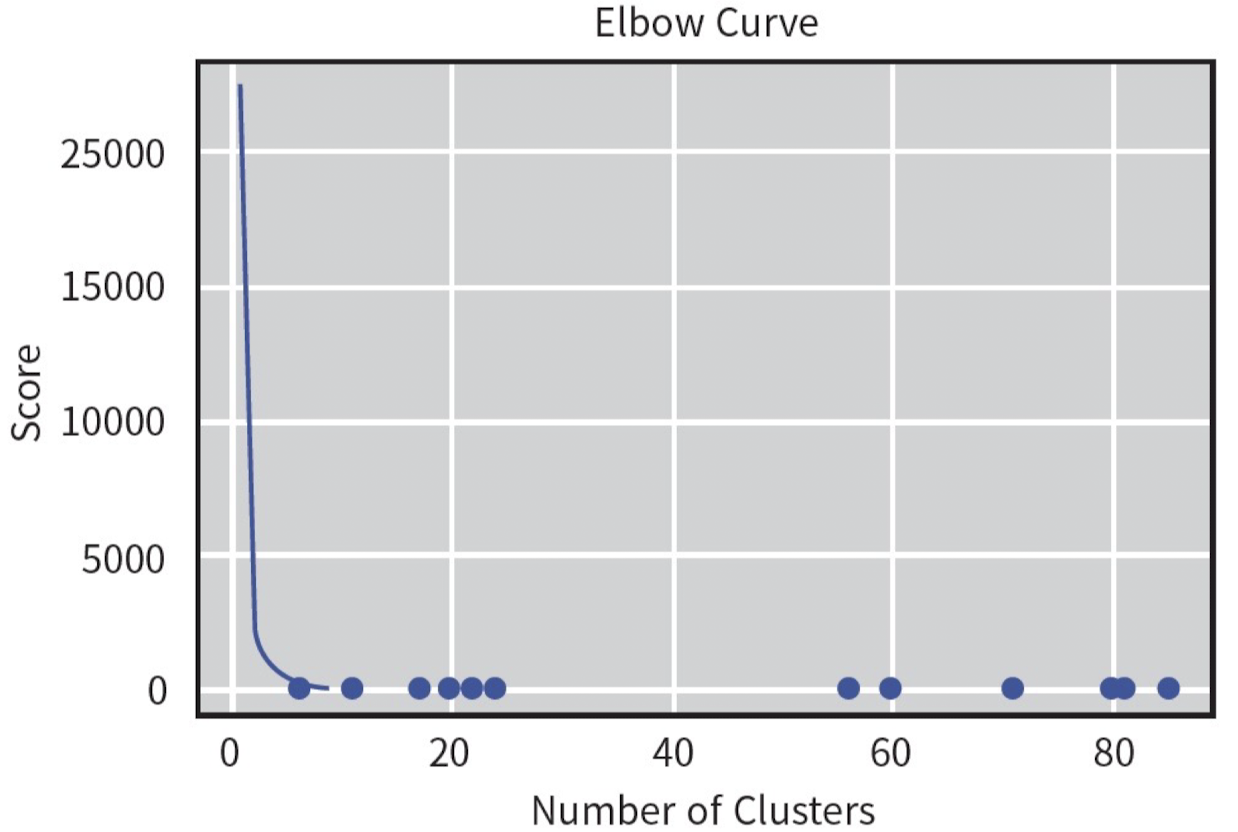
위의 코드를 실행하면 나오는 결과이다. 이때, Score(SSE)가 급격하게 줄어드는 Elbow Curve를 찾을 수 있고, 이 Elbow Curve 지점에서의 Number of Clusters를 K값으로 결정하는 것이다.
K-means의 장단점
장점
- 간단하고 빠르다.
- 수렴을 보장한다.
- 일반화가 쉽다. (새로운 데이터에 적용되기 쉽다.)
단점
-
K를 고르기 위해 노력을 기울여야 한다.
-
시작점에 민감하다. (최초의 Centroid에 따라 최종 Clustering이 달라진다.)
-
Outliers에 민감하다. (평균에서 멀리 떨어진 Outlier들에 의해 영향을 많이 받는다.)
해결책 : 평균값이 아닌 중앙값(Median)을 사용하면 Outlier의 영향을 적게 받을 수 있음.
ex. 평균 제곱 오차를 사용하는 L2 Distance 대신 중앙값을 사용하는 L1 Distance을 사용하면 Outlier의 영향을 적게 받을 수 있다.
PCA(Principle Component Analysis)
Curse of Dimensionality (차원의 저주)
KNN을 공부할 때 계산량이 너무 많다는 단점을 다뤘다. 계산량은 데이터의 차원이 높아질수록 점점 더 많아진다.

예를 들어, 위와 같은 영상 파일의 경우 Width x Height x Frames x RGB 만큼의 차원이기 때문에 데이터의 차원이 매우 크다. 이 경우 계산량이 매우 크고 계산 속도가 매우 느릴 것이다.
따라서 우리는 머신러닝의 성능은 어느 정도 유지하면서 데이터의 차원을 낮추고 싶다.
PCA란?
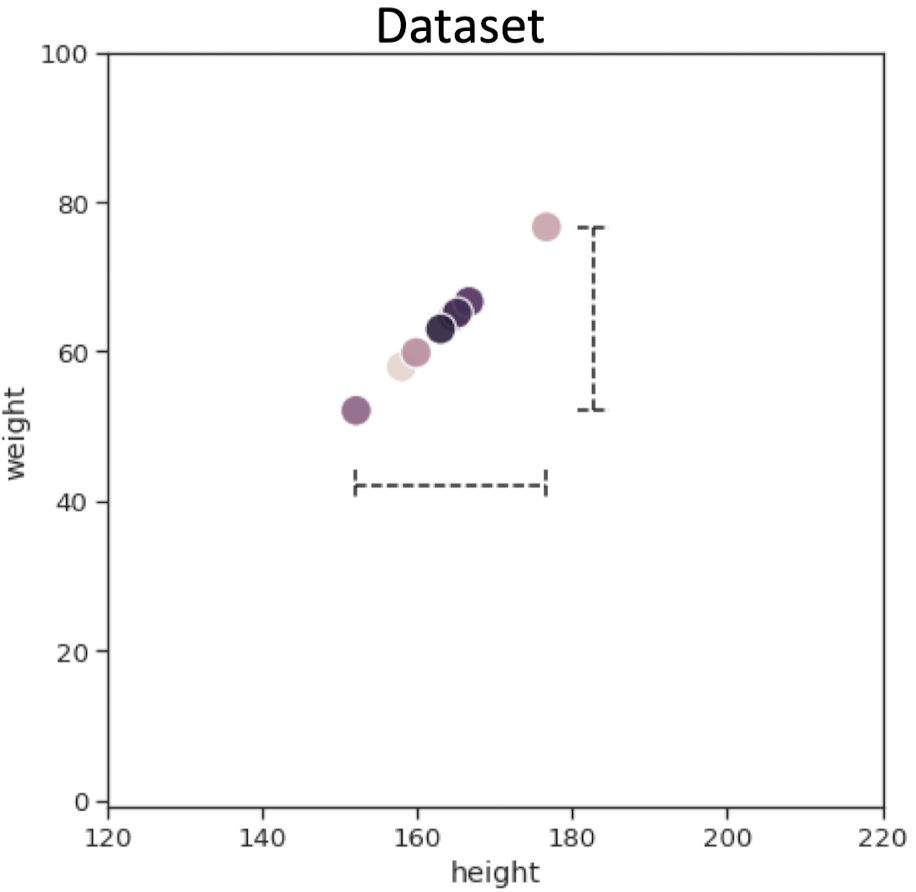
위 그림처럼 완벽하게 정렬된 데이터셋이 있다고 가정하자.
이 경우 오른쪽 맨 위의 데이터를 x, y축 Basis Vector로 표현하면 다음과 같다.
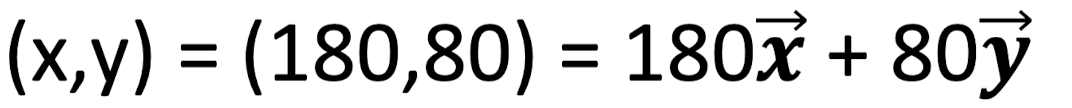
이때 Data Align에 따라 Principal Component(주성분)을 새로 설정해보자.

새로 설정한 Principal Component를 새로운 축으로 하여 데이터를 재정렬하면 오른쪽 그림과 같이 데이터들이 PC1 축에 평행하게 정렬된다. 이 경우 벡터 합으로 표현하면 다음과 같다.
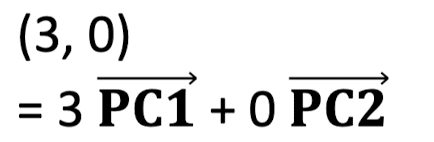
재정렬하기 전에 비해 한 차원 감소한 것을 알 수 있다.
이렇게 Principal Component을 재설정함으로써 데이터를 더 낮은 차원으로 표현하는 방식이 PCA이다.
하지만, 실제 데이터셋은 보통 완벽하게 정렬되어 있지 않다. 이 경우에도 여전히 PCA를 사용할 수 있다. 그렇다면 Principal Component을 어떻게 정할 수 있을까?
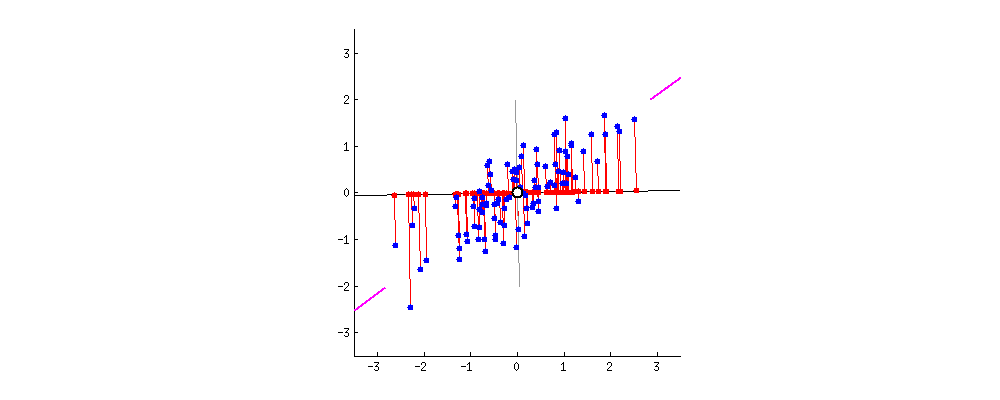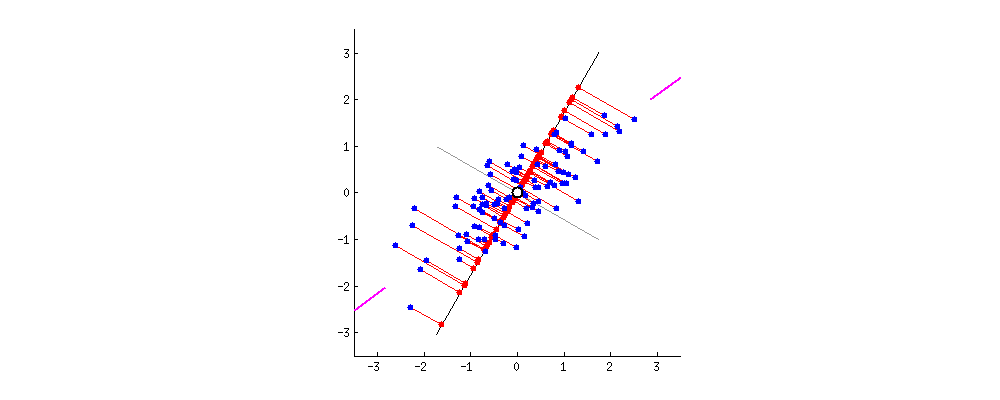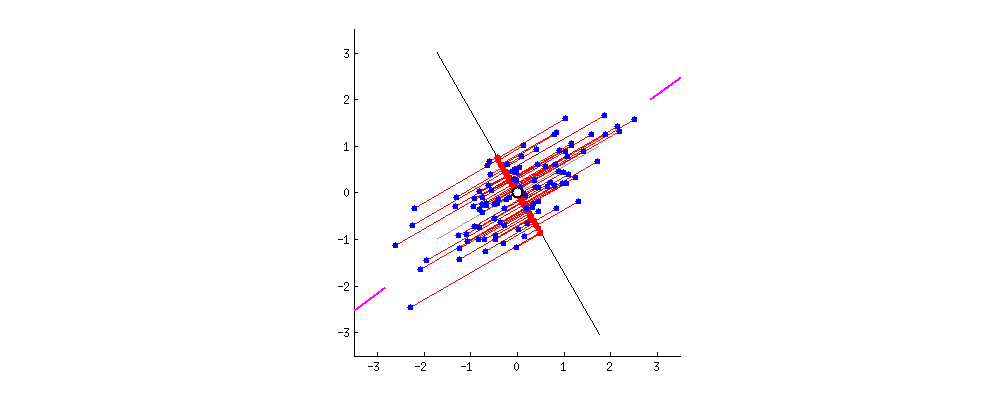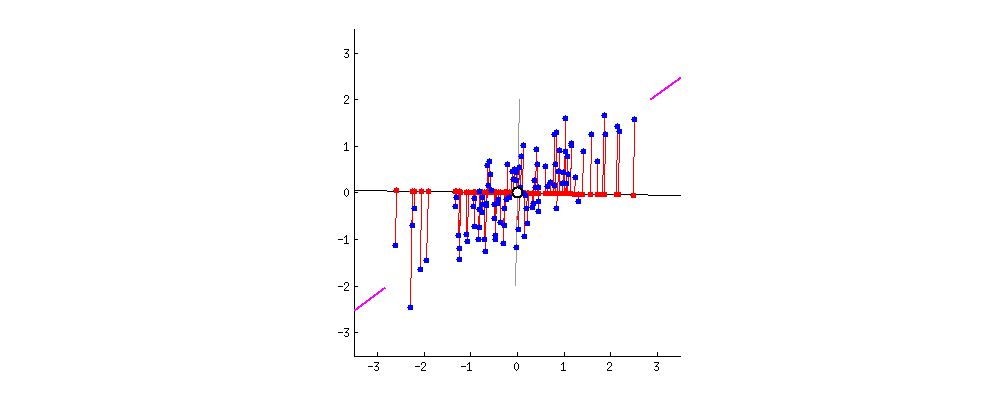
바로, SSE를 최소로 만드는 벡터를 찾아 Principal Component로 정한다.
위의 GIF는 그 과정을 보여준다.
PCA는 행렬곱 연산이며, 다음과 같은 수식으로 나타낼 수 있다.
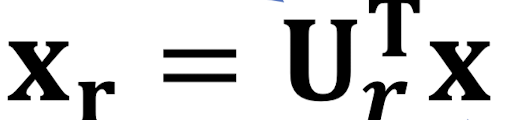
이때 X_r은 PCA를 통해 차원이 감소한 데이터, U는 Principal Component Vector의 행렬, X는 원본 데이터이다.
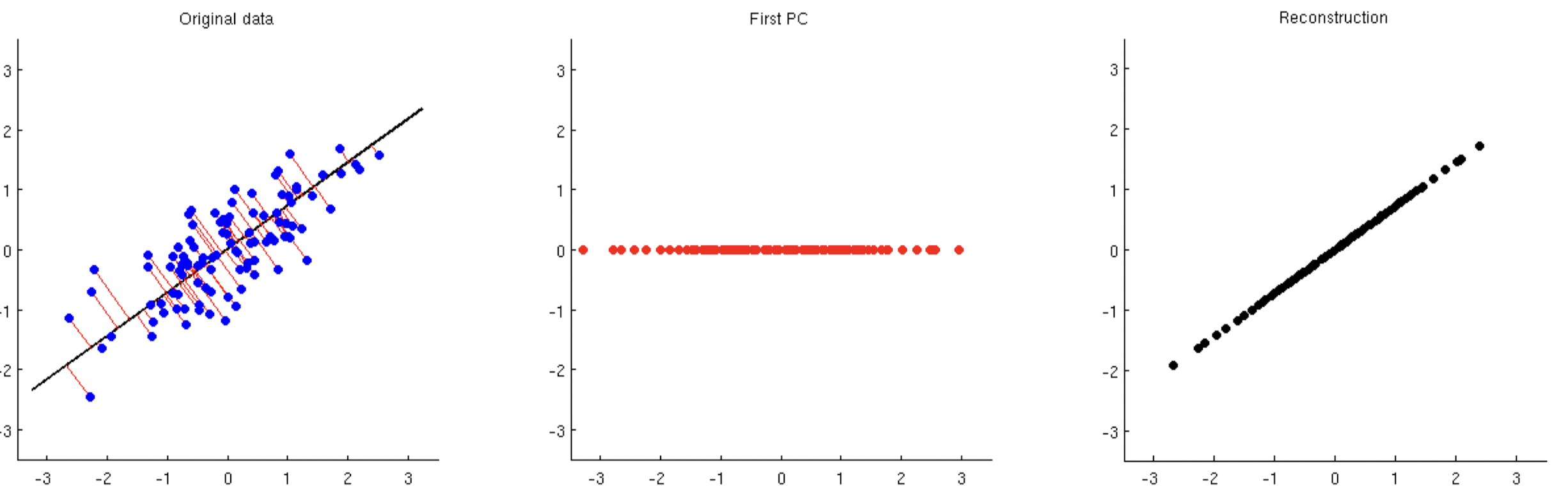
PC를 거친 이후에 데이터의 중요한 정보를 최대한 보존하기 위해 Reconstruction을 통해 Basis Vector을 축으로 하는 좌표 평면에Projection한다.
PCA 성능
K-nearest neighbor with MNIST
• Originally (784 dimensions x 60,000 training data):
• Accuracy: 96.9
• Running time: 1 minutes
After PCA (10 dimensions x 60,000 training data):
• Accuracy: 92.8
• Running time: 1.5 sec
위의 지표는 MNIST 데이터에 대해 KNN을 PCA를 사용하지 않고 수행했을 때와 PCA를 사용해서 수행했을 때의 Accuracy와 Running Time 수치를 나타내고 있다.
이때 PCA를 통해 수행했을 때는 차원이 784에서 10으로 많이 줄어든 것을 확인할 수 있다. 또, Accuracy가 4.1% 감소했지만, Running Time은 약 40배 가량 감소한 것을 확인할 수 있다. PCA를 사용하면 정확도는 조금 낮아지지만 속도는 훨씬 빨라진다는 것을 알 수 있다.
PCA 사용 분야
• 차원 축소 : 데이터 크기를 줄여서 Computation Time을 감소시킬 수 있음.
• 이미지 압축 : 메모리 사용을 줄이고, PCA는 선형 기법 중에 Loss가 가장 작은 기법이다.
• Noise 제거 : 이미지 데이터의 Noise를 제거할 수 있다. (Denoising)

PCA의 한계점
PCA의 한계점은 PCA가 Orthogonal Basis(직교 기반)라는 점에서 나타난다.
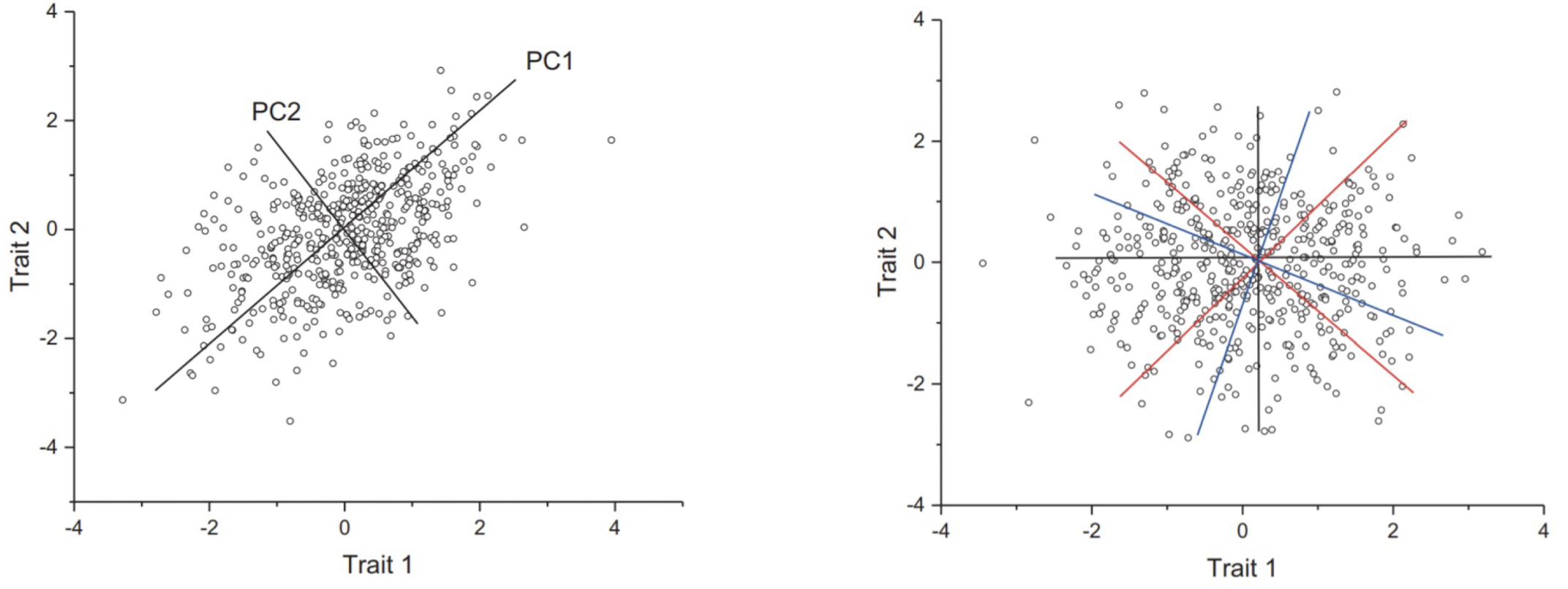
왼쪽 그림의 데이터는 어느 정도 선형으로 정렬되어 있기 때문에 PCA를 통해 차원 축소를 하는 것이 의미 있을 수 있다.
반면, 오른쪽 그림의 데이터 분포에서는 직교하는 PC 성분을 통해 차원 축소를 하는 것이 거의 무의미할 정도로 무질서하게 정렬되어 있다. 따라서 PCA는 항상 최선의 방법은 아니다.
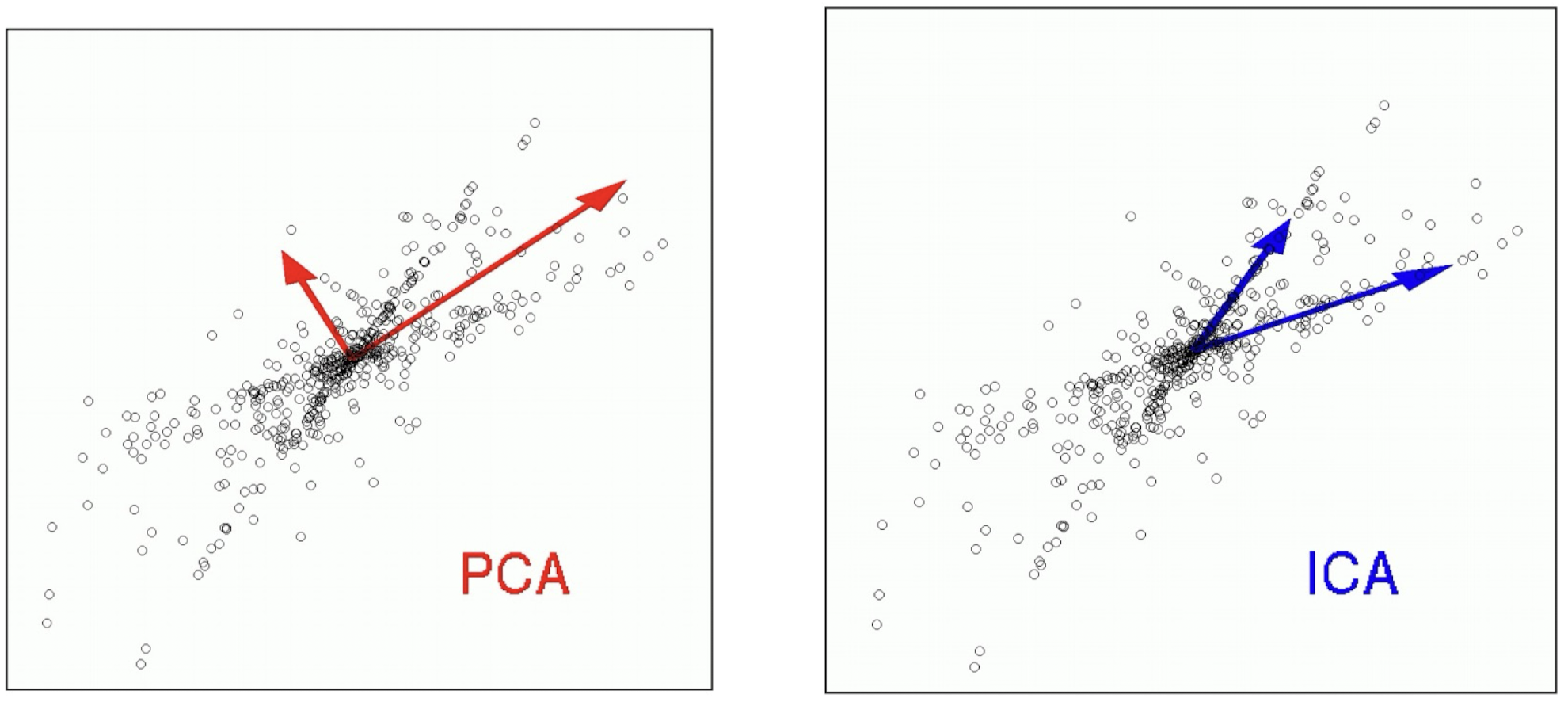
데이터를 가장 잘 설명할 수 있는 축을 찾는 PCA 알고리즘과는 달리,
독립성이 최대가 되는 축을 찾으며, 기준 축이 반드시 직교할 필요가 없는 ICA(Independent Component Analysis, 독립 성분 분석) 알고리즘도 있다.
