문제

이항 계수 2
이항 계수 3

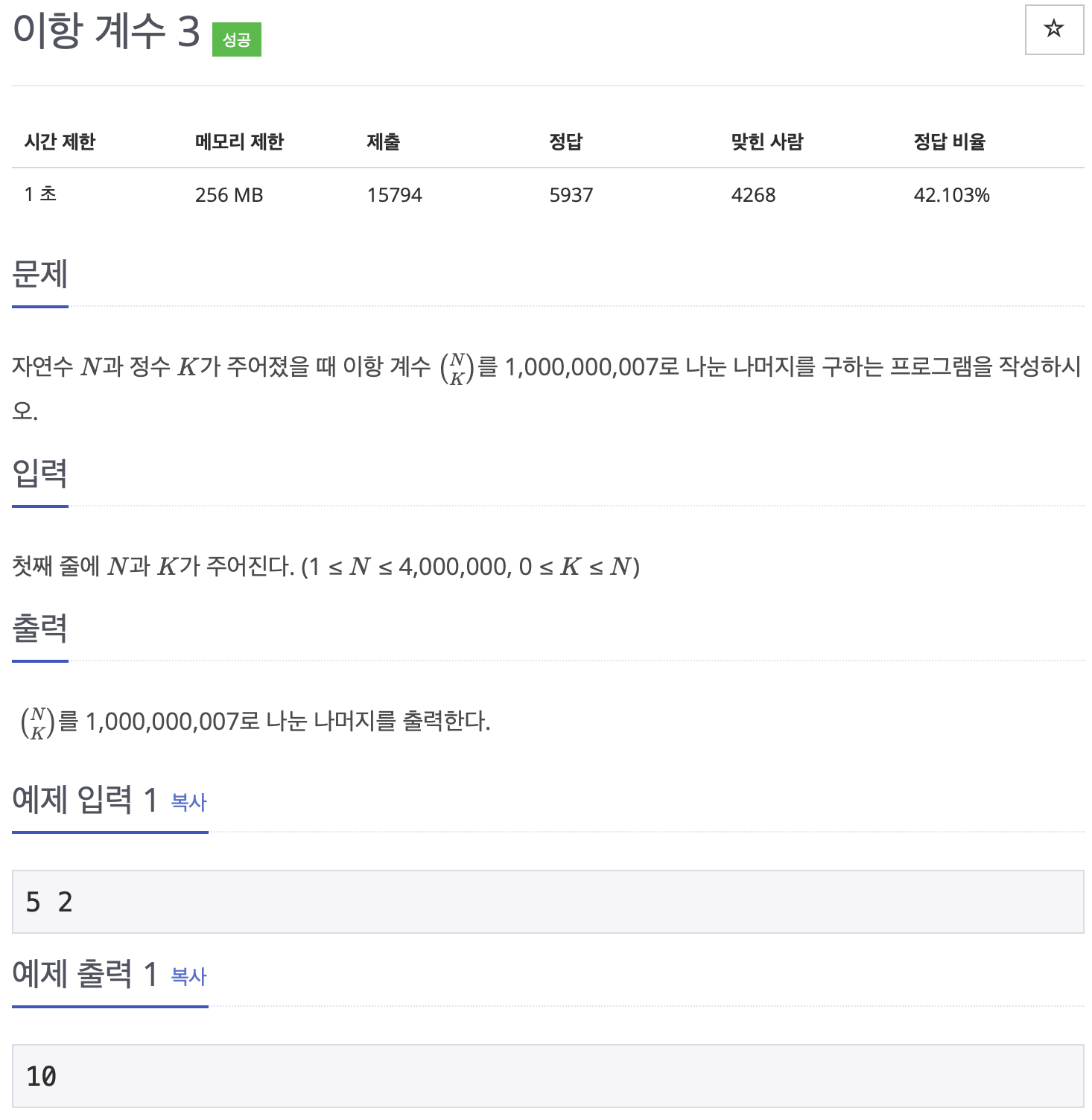
설명

문제는 2나 3이나 비슷하다.
그러나 크기가 많이 다르다.
2는 간단한 DP로 해결가능하다.
3은 nCk를 적당한 소수로 모듈로 연산한 결과를 출력하는 문제다.
이 문제도 처음에 DP로 접근하였으나 몇가지 다른 스킬들이 필요하다.

페르마의 소정리

세 수식을 각각 a, b, c라고 하자
P가 소수이고, B와 P가 서로소일때 a가 성립한다.

모듈로 곱셈 역원

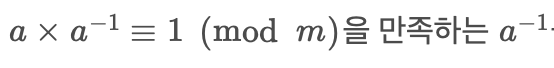
백준님 게시글에 정리가 잘 되어있다.

역원은 어떤 수와 또다른 수를 곱했을 때, 값을 1로 만드는 또다른 수다.

a를 변형한 b 를 보면
B * B^(p-2) = 1(mod P)
그러므로 B^(p-2) 가 B의 역원이라고 할 수 있다.

분할정복을 이용한 제곱

적용

페르마의 소정리를 사용해 다음과 같이 나타낼 수 있다.

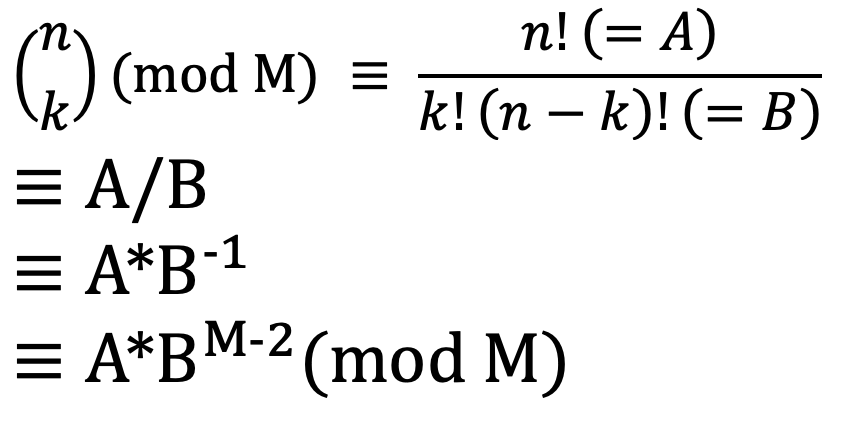
따라서 나누기 대신 제곱만 사용해 문제를 해결할 수 있게 된다.
(안타깝게도 팩토리얼은 계산해야 한다)

코드

// 2022.02.27 14:45:10
// 11401 https://boj.kr/11401
#include <bits/stdc++.h>
#define M 1'000'000'007
using namespace std;

long long f(long long num, long long pow)
{
    if (pow == 1)
        return num % M;

    long long x = f(num, pow / 2);
    x = (x * x) % M;
    if (pow % 2 == 0)
        return x;
    return x * num % M;
}

// nCk =       n!  ( = A )
//       ---------------
//        k! * (n-k)! ( = B )
// = A/B mod M
// = A*B^(-1) mod M
// = A*B^(M-2) mod M
long long bi(long long n, long long k)
{
    long long A = 1, B = 1;
    for (long long i = 1; i <= n; i++)
    {
        A *= i;
        A %= M;
    }
    for (long long i = 1; i <= k; i++)
    {
        B *= i;
        B %= M;
    }
    for (long long i = 1; i <= n - k; i++)
    {
        B *= i;
        B %= M;
    }

    return (A * f(B, M - 2)) % M;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);

    long long n, k;
    cin >> n >> k;

    cout << bi(n, k);
}