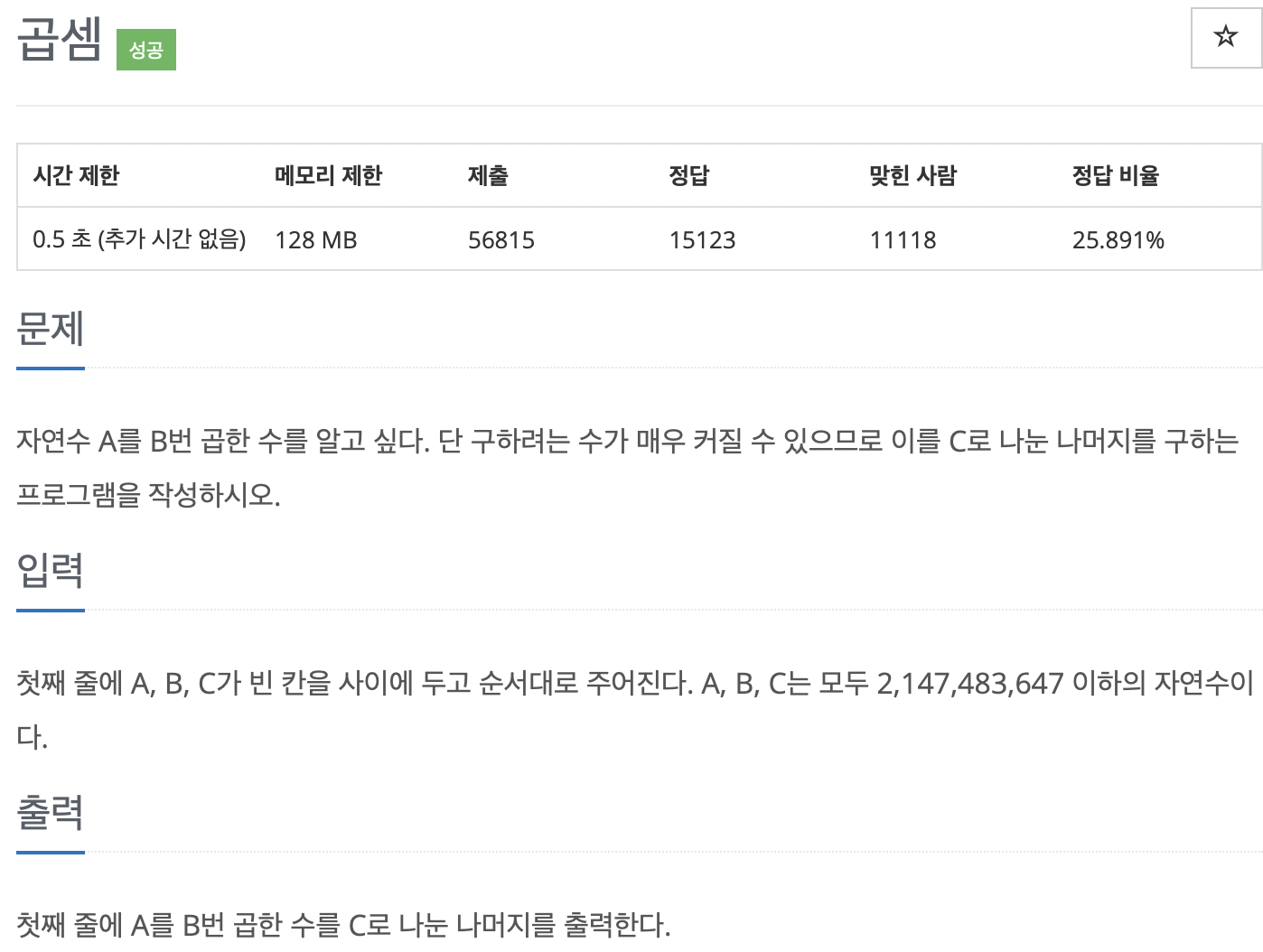
문제
설명
컴퓨터의 정수형이 소수점 아래를 표현하지 못하는 점을 고려할 때,
어떤 수의 거듭제곱은 다음과 같이 나타낼 수 있다.
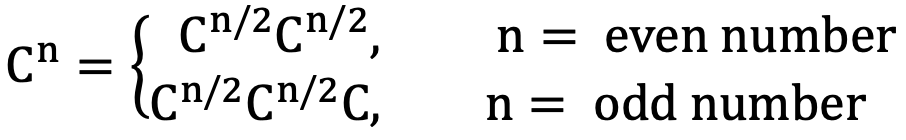
상단 식은 n이 짝수인 경우, 하단 식은 홀수인 경우이다.
이 점을 이용해 분할정복 알고리즘을 사용하면, 매번 문제의 크기가 1/2로 줄어드는 솔루션을 작성할 수 있다.
2^10 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2
9번 계산해야 할 것이
2^10 = 2^5 * 2^5,
2^5 = 2^2 * 2^2 * 2
2^2 = 2^1 * 2^1
2^1 = 1 * 1 * 2
으로 6번만에 끝나게 된다.
(수가 커지면 더 의미있게 작아진다)
코드
// 2022.02.27 16:40:29
// 1629 https://boj.kr/1629
#include <bits/stdc++.h>
using namespace std;
int a, b, c;
// O(logn), 문제 크기가 매번 절반으로 줄어듦.
int fpow(int n)
{
if (n == 1)
return a % c;
int x = fpow(n / 2);
x = ((long long)x * x) % c;
if (n % 2 == 0)
{
return x;
}
else
{
return ((long long)x * a) % c;
}
}
int main()
{
cin.tie(0);
ios::sync_with_stdio(false);
cin >> a >> b >> c;
cout << fpow(b);
}