🏖️ 1. 그래프 신경망(GNN) - Part 2
이번 파트에서는 GNN의 레이어 구조와 주요 GNN 모델의 차이점에 대해 알아보겠다. 그래프 신경망의 핵심은 Message 전달 함수와 Aggregation 함수로 구성된 레이어 구조이다. 이 구조는 다양한 GNN 모델에서 공통적으로 사용되며, 각 모델의 차이는 주로 메시지 전달 방법과 집계 함수에서 발생한다.
1. GNN Layer
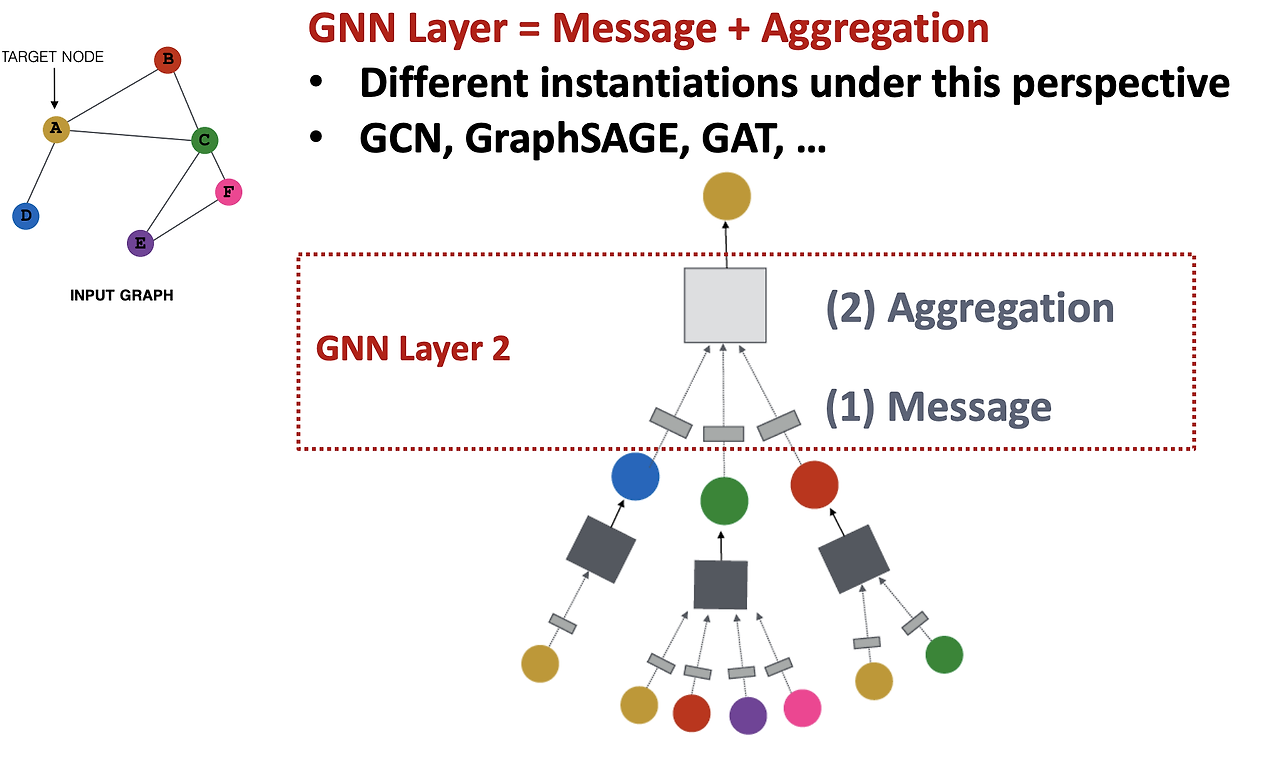
GNN의 기본 레이어는 다음 두 가지 요소로 구성된다.
- Message 함수
메시지 함수는 각 노드로부터 이웃 노드로 전달될 메시지를 생성하는 함수이다. 이는 주로 선형 변환으로 표현되며, 이전 레이어의 특성에 가중치 행렬 W를 곱하여 메시지를 생성한다.
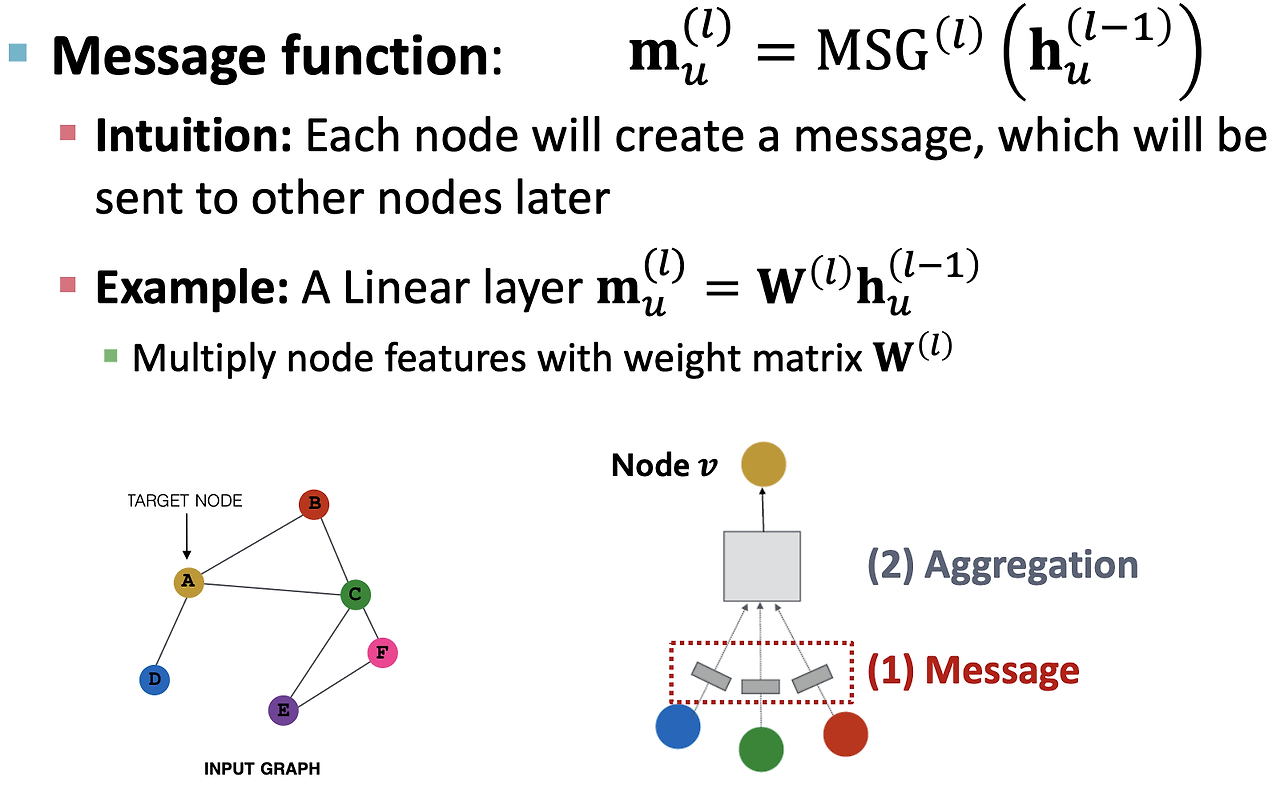
- Aggregation 함수
Aggregation 함수는 이웃 노드들의 메시지를 요약하여 각 노드의 임베딩을 업데이트하는 함수이다. 이를 통해 이웃 노드들의 정보를 집계하며, 주로 평균(mean), 합(sum), 최대 풀링(max-pooling) 등의 방법이 사용된다.
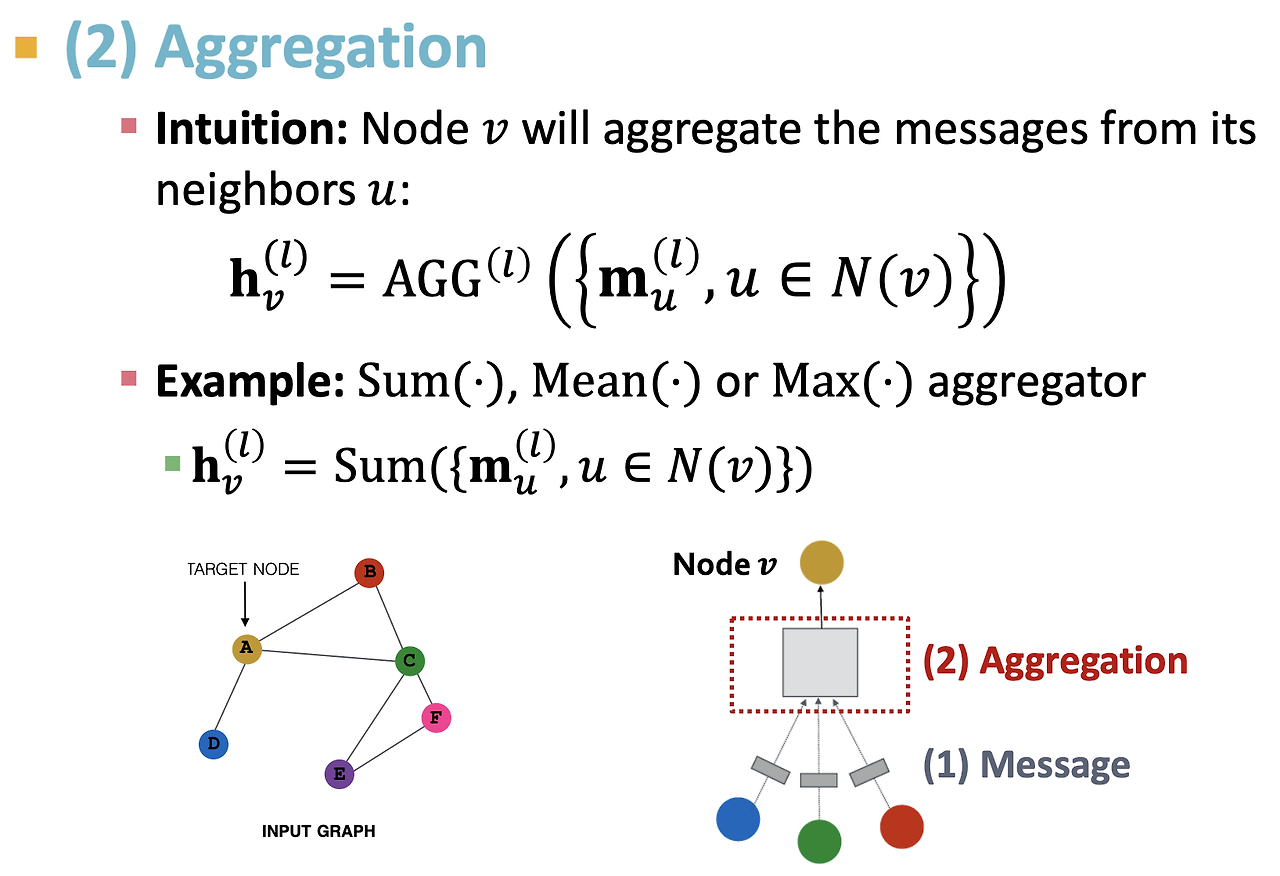
2. GNN Layer의 메시지 및 집계 과정
메시지 전달:
예를 들어, 노드 A의 이웃 노드가 B, C, D일 때, 이 노드들의 임베딩 벡터에 가중치 행렬을 곱한 값을 메시지로 생성한다.
집계 과정:
이후 이 메시지들을 평균, 합, 혹은 최대값을 사용하여 요약한 후, 노드 A의 임베딩을 업데이트한다. 이때 자기 자신(A 노드)에 대한 정보가 유실되지 않도록, 자기 자신에 대한 정보도 함께 집계한다.
문제점
만약 자기 자신에 대한 정보를 포함하지 않고 이웃 노드의 정보만 사용한다면, 각 노드가 가진 고유한 정보가 손실될 수 있다.
해결 방법
자기 자신에 대한 정보를 업데이트하는 행렬 B와 이웃 노드 정보를 업데이트하는 가중치 행렬 W를 통해 두 가지 정보를 모두 반영한 후 합친다.
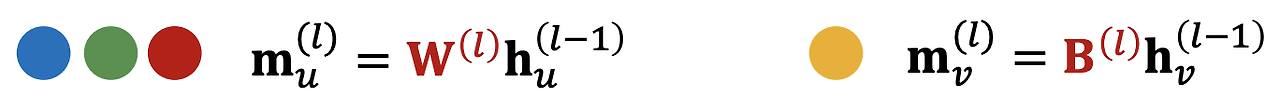
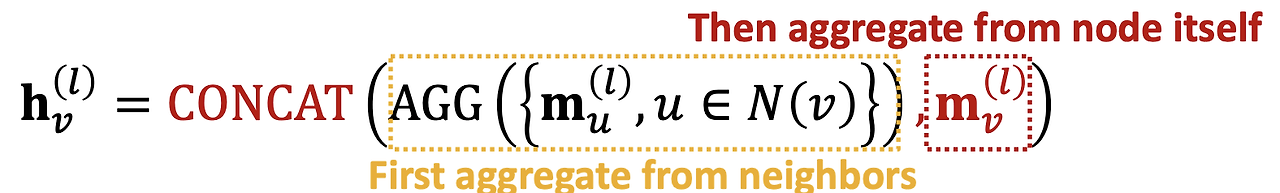
최종적인 기존의 GCN 레이어의 모습은 아래와 같다.
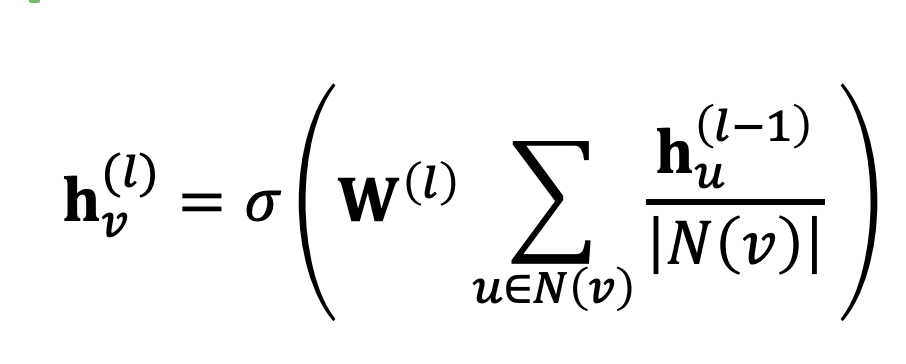
- 이웃 노드들의 임베딩을 먼저 평균 내고 (∑{𝑢∈𝑁(𝑣)} 𝐡𝑢^((𝑙−1))/|𝑁(𝑣)|), 그 결과에 가중치 행렬 𝐖^((𝑙))를 곱한다.
- 즉, 집계된 메시지에 한 번의 선형 변환을 수행하는 셈이다.
- 모든 이웃 노드들의 임베딩이 동일한 가중치 행렬에 의해 변환된다.
🏖️ 2. GNN Layer 종류
1. GCN (Graph Convolutional Network)
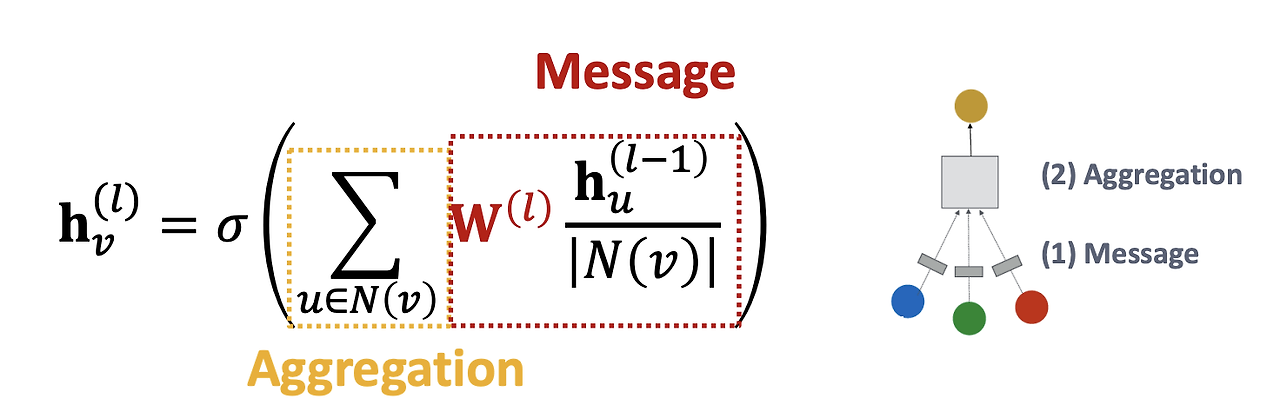
GCN은 이웃 노드의 임베딩을 평균 내고, 그 결과에 가중치 행렬 W를 곱하는 방식이다. 모든 이웃 노드들의 임베딩에 동일한 가중치 행렬이 적용되며, 노드의 특징은 이웃 노드들의 정보를 집계한 후 선형 변환을 통해 업데이트된다.
주요 특징
- 효율성: 이웃 노드들의 메시지를 한 번에 합치고 선형 변환을 수행하므로 계산 효율이 높다.
- 표현력: 각 이웃 노드의 정보를 세밀하게 반영하기보다는 모든 이웃의 정보를 평균하여 처리한다. 이는 표현력 측면에서는 다소 제한적일 수 있다.
2. Graph SAGE
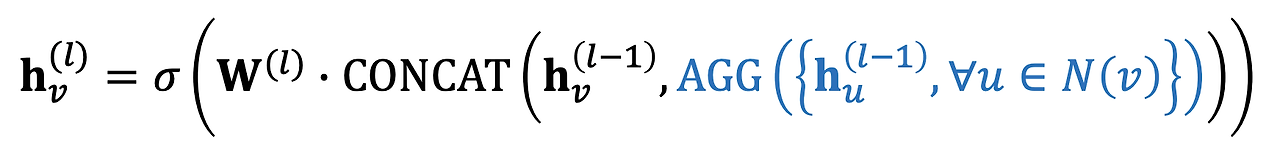
Graph SAGE는 GCN의 변형된 방식으로, 각 노드의 임베딩을 업데이트할 때 자기 자신의 정보를 포함한다. 이때 집계 함수로 Mean, Pool, LSTM 등을 자유롭게 사용할 수 있다.
집계 함수 종류
- Mean: 이웃 노드들의 임베딩을 단순 평균한 값을 사용한다.
- Pool: 각 이웃의 임베딩에 MLP(Multi-Layer Perceptron)를 적용하고, 변환된 임베딩 중 최대값을 선택하여 집계한다.
- LSTM: 이웃 노드 임베딩을 순차적으로 입력하여 LSTM을 통해 순서 정보를 반영하며 집계한다.
주요 특징
Graph SAGE는 이웃 노드 정보와 자기 자신의 정보를 함께 고려하여 임베딩을 업데이트하며, 다양한 집계 함수를 통해 유연한 집계 방식을 제공한다.

3. GAT (Graph Attention Network)

GAT는 이웃 노드의 중요도를 고려하는 Attention 메커니즘을 사용하는 GNN 모델이다. 각 이웃 노드의 임베딩에 동일한 가중치를 적용하는 대신, 각 이웃 노드의 중요도에 따라 가중치를 다르게 적용한다.
Attention 계수 계산
노드 A와 이웃 B, C, D 사이의 Attention 계수는 노드 임베딩에 가중치 행렬을 곱한 후 Attention 함수를 통해 계산된다. 이 계수는 각 이웃 노드가 A 노드의 임베딩 계산에 기여하는 정도를 나타낸다.
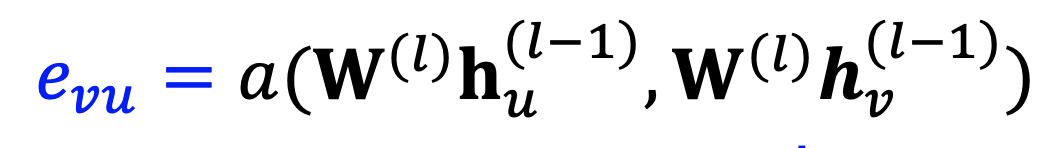
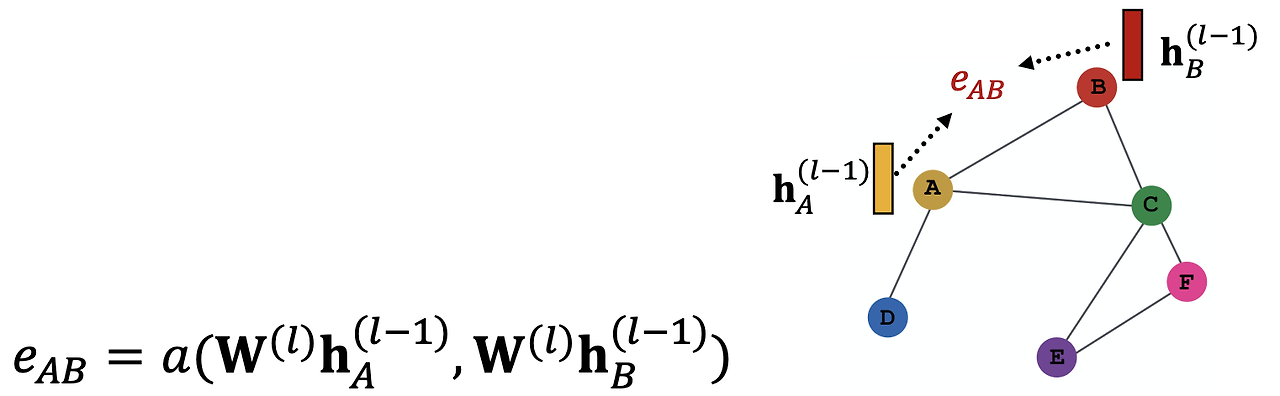
Multi-head Attention
GAT에서는 다양한 관점에서 노드 간의 중요도를 평가하기 위해 Multi-head Attention을 사용한다. 여러 개의 Attention 메커니즘을 병렬로 적용하여, 각 이웃 노드의 중요도를 다양한 방식으로 평가할 수 있다.
주요 특징
- 유연성: 이웃 노드의 중요도에 따라 가중치를 부여하므로, 더 중요한 노드의 정보가 더 많이 반영된다.
- 확장성: Multi-head Attention을 통해 다양한 관점에서 이웃 노드를 평가할 수 있다.
GGNN과 HGNN의 핵심 개념에 대해 설명을 추가해드리겠습니다.
4. GGNN (Graph Gated Neural Network)
GGNN은 순환 신경망(RNN)의 GRU(Gated Recurrent Unit)을 그래프에 적용한 모델로, 그래프 구조에서 message passing을 통해 노드 간의 정보를 주고받고, 이를 통해 노드 임베딩을 학습합니다.
주요 특징:
- Message Passing: 각 노드가 인접 노드들과 정보를 주고받는 과정을 통해 노드 임베딩을 업데이트합니다. 이는 그래프의 구조적 정보를 더 잘 반영할 수 있게 합니다.
- GRU 적용: GRU는 RNN의 일종으로, 노드의 정보가 업데이트될 때, 이전 상태와 새로운 정보를 함께 고려하여 중요한 정보를 유지하고 불필요한 정보를 제거하는 게이트 메커니즘을 사용합니다. 이로 인해 그래프의 상태가 동적으로 변하는 상황에서 유용합니다.
- 적합한 문제: GGNN은 시계열 또는 순차적인 그래프 데이터를 처리하거나, 노드 간의 복잡한 의존성을 학습할 때 효과적입니다.
5. HGNN (Hypergraph Neural Network)
HGNN은 하이퍼그래프를 기반으로 한 신경망으로, 하이퍼엣지를 사용하여 여러 노드 간의 복잡한 관계를 동시에 표현할 수 있습니다. 일반적인 그래프에서는 엣지가 두 노드만 연결하지만, 하이퍼그래프에서는 엣지가 여러 노드를 연결할 수 있습니다.
주요 특징:
- 하이퍼그래프 구조: 일반 그래프에서는 한 엣지가 두 개의 노드를 연결하지만, 하이퍼그래프는 한 엣지가 여러 개의 노드를 동시에 연결할 수 있습니다. 이로 인해 복잡한 다중 관계를 표현하는 데 적합합니다.
- 다중 모달 데이터: 다양한 유형의 데이터(예: 텍스트, 이미지, 시계열 등)를 함께 처리해야 하는 경우나, 복잡한 상관관계를 갖는 데이터를 다루는 문제에 적합합니다.
- 적합한 문제: 여러 노드들 사이의 복잡한 상호작용을 학습해야 하거나, 고차원적인 관계를 분석할 때 효과적입니다.
🏖️ 정리
GNN Layer의 기본 구성
- GNN 레이어는 Message 함수와 Aggregation 함수로 구성된다. 각 모델은 메시지 전달 및 집계 방식을 다르게 하여 다양한 그래프 구조에 맞는 임베딩을 학습할 수 있다.
GNN Layer 종류
- GCN: 이웃 노드 임베딩을 평균하여 가중치 행렬을 적용하는 방식. 계산 효율성이 높다.
- Graph SAGE: 자기 자신의 정보를 포함하여 임베딩을 업데이트하며, 다양한 집계 함수를 사용할 수 있다.
- GAT: Attention 메커니즘을 통해 이웃 노드의 중요도를 고려하여 임베딩을 계산한다. Multi-head Attention을 사용하여 표현력을 높인다.
GNN Layer의 설계는 문제의 특성에 맞게 선택할 수 있으며, 각 모델은 서로 다른 장점과 효율성을 제공한다.
