🏖️ 노드 임베딩(Node Embedding)
노드 임베딩은 그래프의 각 노드를 저차원 벡터로 표현하는 기법이다. 이는 그래프 데이터에서 노드의 관계와 구조를 벡터 공간에 반영하여 여러 머신러닝 태스크에서 활용할 수 있게 한다. 대표적으로 노드 분류(Node Classification), 링크 예측(Link Prediction), 그래프 분류(Graph Classification) 등 다양한 작업에 사용된다.
1. 전통적인 방식의 노드 임베딩
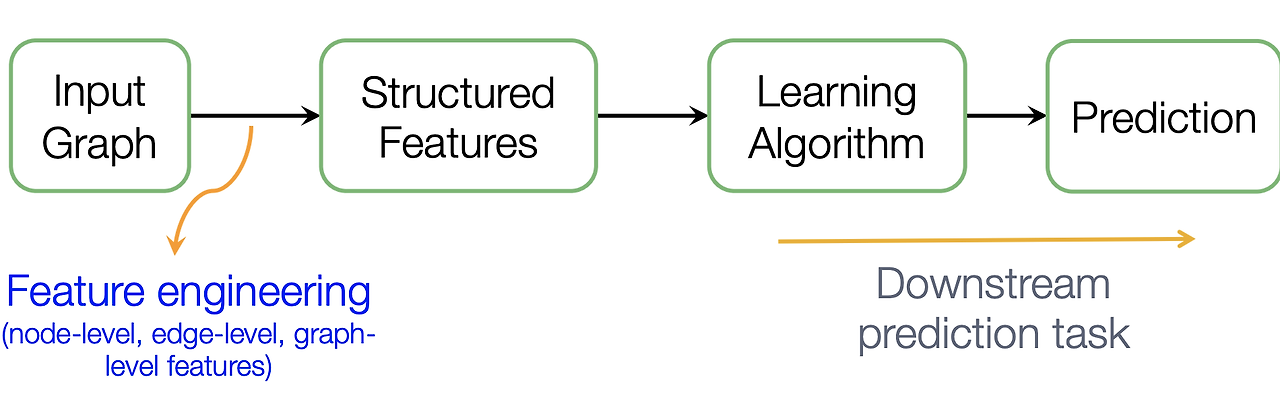
초기 머신러닝 모델에서는 Feature Engineering이 매우 중요한 역할을 했다. 노드 임베딩을 사용하기 전, 그래프의 각 노드를 특징(feature)으로 표현하기 위해서는 그래프의 구조적 특성이나 노드 간의 관계를 일일이 정의해야 했다. 이 방식은 주로 수작업으로 이루어졌으며, 모든 특성을 명시적으로 추출해야 했다.
- 특성 공학 (Feature Engineering):
각 노드에 대해 명시적으로 다양한 특성을 추출하고, 이를 모델에 적용하는 방식이다. 이 과정은 매우 복잡하고 많은 노력을 요구한다.
2. 그래프의 표현학습
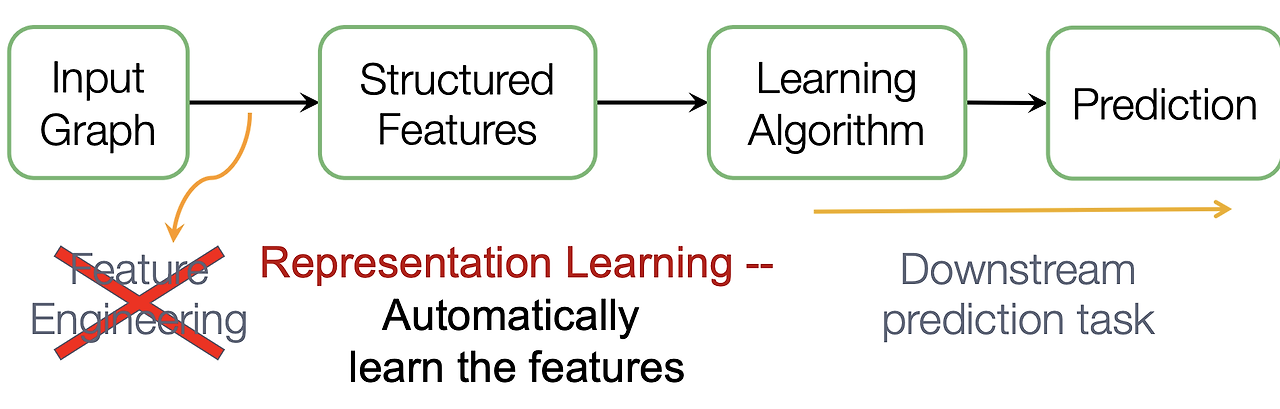
표현 학습(Representation Learning)의 목표는 그래프에서 유용한 특성을 자동으로 학습하는 것이다. 이를 통해, 기존의 수작업으로 이루어지던 특성 공학의 단점을 극복할 수 있다. 노드 임베딩은 이러한 표현 학습의 일환으로, 그래프에서 각 노드를 의미 있는 벡터로 변환하여 노드 간의 유사성이나 관계를 모델링할 수 있다.
- 그래프 표현 학습의 중요성:
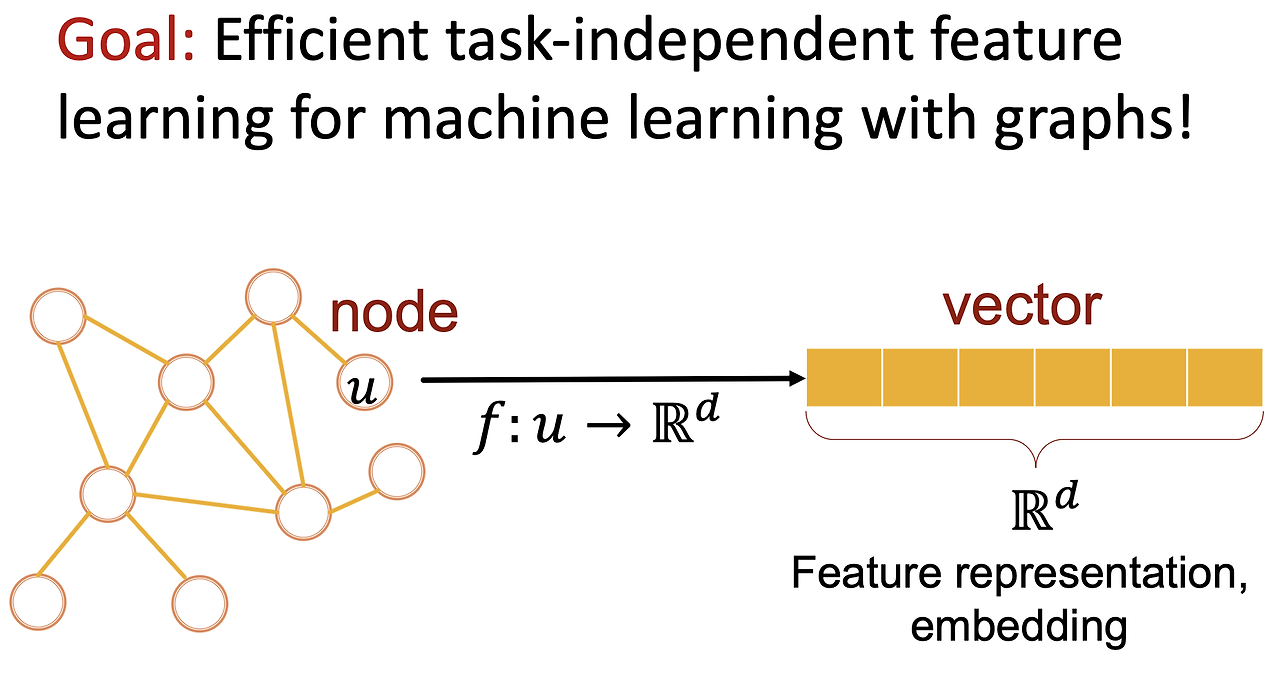
노드 임베딩을 사용하면 그래프의 복잡한 구조와 관계를 벡터 공간에서 효율적으로 표현할 수 있다. 이는 그래프 기반의 다양한 머신러닝 문제를 해결하는 데 매우 유용하다.

🏖️ 노드 임베딩: 인코더와 디코더
노드 임베딩의 핵심은 그래프에 있는 노드들을 저차원 벡터 공간으로 맵핑하는 것이다. 이는 인코더(Encoder)와 디코더(Decoder)라는 두 가지 주요 구성 요소를 통해 이루어진다.
1. 인코더 (Encoder)
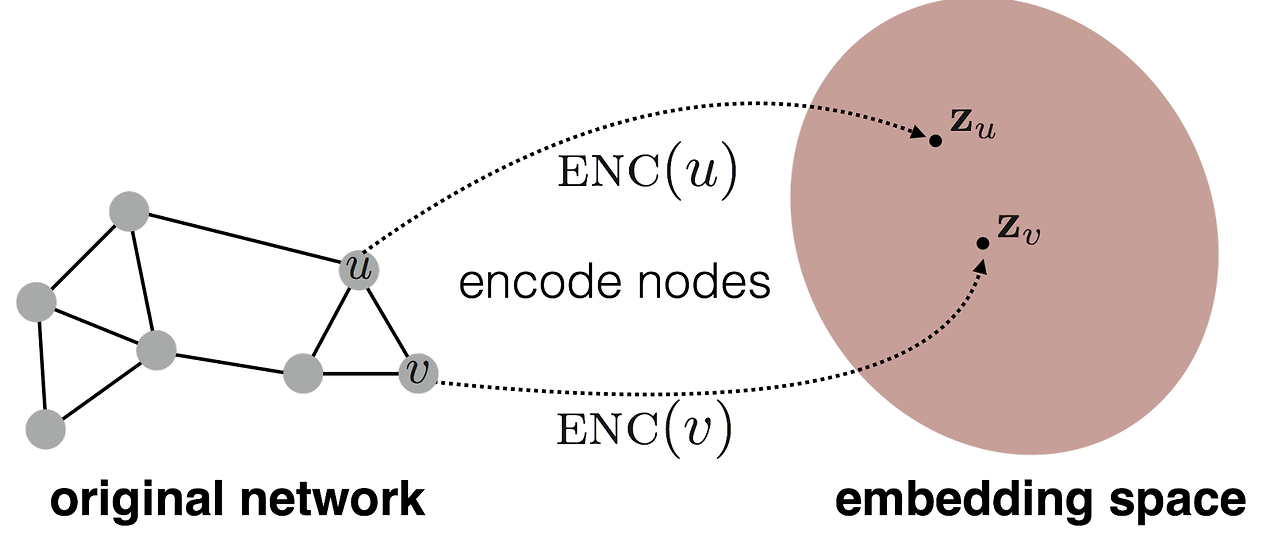
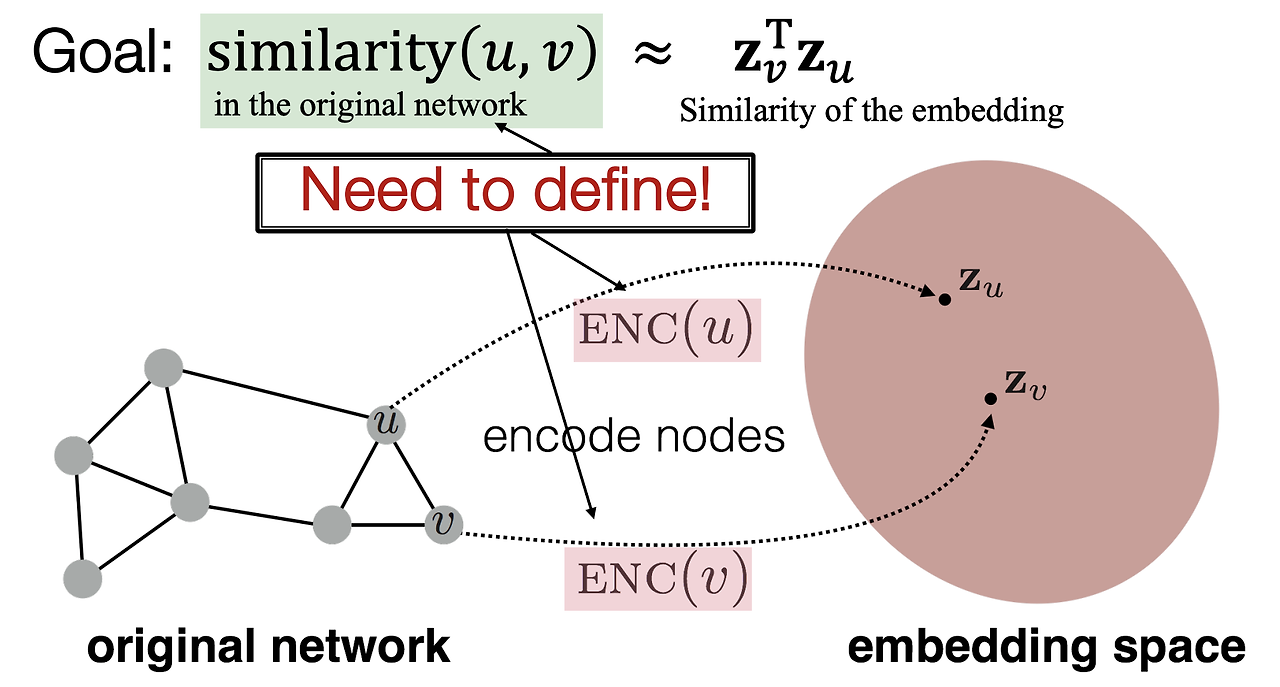
인코더의 역할은 원본 그래프에서 각 노드를 임베딩 공간인 Z 공간으로 맵핑하는 것이다. 하지만 단순히 노드를 벡터로 변환하는 것이 아니라, 노드 간의 유사성이 Z 공간에서 유지되도록 맵핑하는 것이 중요하다. 즉, 그래프 상에서 노드 간의 유사도를 반영한 벡터 공간을 형성하는 것이 목표이다.
- 인코딩 과정:
노드 (U)와 (V)가 원본 그래프에서 유사하다면, 이들 노드가 임베딩된 (Z(U))와 (Z(V)) 역시 가까운 벡터로 표현되어야 한다. - 유사도 측정:
그래프 상에서 노드 간의 유사도를 측정하는 다양한 방법을 사용할 수 있다. 이를 바탕으로 임베딩 공간에서의 유사도와 원본 그래프에서의 유사도를 최대한 비슷하게 만드는 것이 인코더의 목표이다.
2. 디코더 (Decoder)
디코더는 인코더가 만들어낸 임베딩 벡터를 바탕으로 노드 간의 유사도를 계산하는 역할을 한다. 이때 디코더는 주로 벡터 간의 내적(dot product)을 사용해 두 노드 간의 유사도를 계산한다.
- 유사도 점수 계산:
임베딩 벡터 (Z(U))와 (Z(V))의 내적을 통해 두 노드의 유사도를 측정할 수 있다. - 파라미터 최적화:
디코더의 목적은 원본 그래프에서의 노드 유사도와 임베딩 공간에서의 유사도가 최대한 비슷해지도록 파라미터를 최적화하는 것이다.
🏖️ 노드의 유사성을 측정하는 방법: Random Walks
Random Walks(랜덤 워크)는 노드 간의 유사성을 측정하는 비지도 학습 방법이다. 이 방법은 노드의 특징이나 라벨을 사용하지 않고, 그래프의 구조적 특성만을 기반으로 노드 간 유사성을 추정한다. 주요 아이디어는 한 노드에서 시작한 랜덤 워크가 다른 노드를 자주 방문하면, 두 노드가 유사하다고 간주하는 것이다.
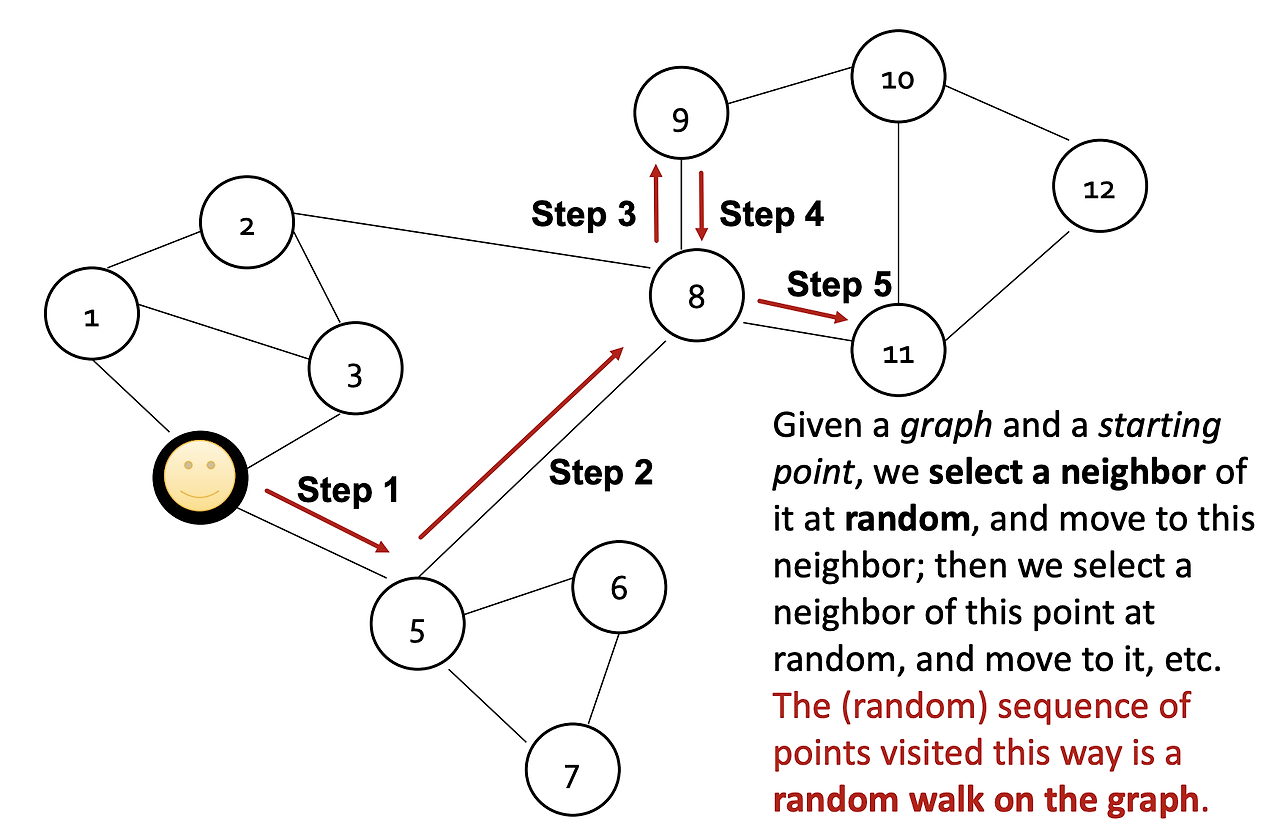
1. 랜덤 워크 시뮬레이션
랜덤 워크는 한 노드에서 시작해 그래프를 따라 이동하는 시뮬레이션이다. 랜덤 워크는 이웃 노드 중 하나를 임의로 선택해 이동하며, 이 과정을 반복한다. 이를 통해 그래프 상에서 서로 가까운 노드들이 더 자주 방문되는 경향을 파악할 수 있다.
예시
사용자 A에서 시작하는 랜덤 워크가 사용자 B를 자주 방문한다면, 사용자 A와 B는 유사하다고 판단할 수 있다. 반대로 사용자 C는 A에서 시작한 랜덤 워크에서 거의 방문되지 않는다면, A와 C는 유사도가 낮다고 볼 수 있다.
2. 방문 확률 모델링
랜덤 워크를 통해 얻은 정보는 각 노드의 임베딩을 학습하는 데 사용된다. 예를 들어, 노드 (Z_A)에서 시작한 랜덤 워크가 노드 (Z_B)를 방문할 확률을 (P(B|Z_A))로 모델링할 수 있다. 이 확률 값은 소프트맥스 함수(softmax function)를 사용해 계산된다.
- 소프트맥스 예시:
(P(B|Z_A) = 0.7), (P(C|Z_A) = 0.01)이라면, 사용자 A와 B가 더 유사하다는 의미가 된다.
3. 노드 임베딩 최적화
노드 임베딩의 학습 목표는 랜덤 워크에서 얻은 유사도를 반영하여 각 노드의 임베딩을 최적화하는 것이다. 이를 위해 확률적 경사 하강법(SGD)을 사용해 임베딩 벡터를 업데이트한다.
- 목적 함수:
노드 A에서 시작한 랜덤 워크에서 방문된 노드 B의 확률을 최대화하는 것이 목적이다. 예를 들어, 목적 함수는 ( \log P(B|Z_A) )와 ( \log P(C|Z_A) ) 등의 항을 최대화하는 방향으로 임베딩을 학습하게 된다.
랜덤 워크 기반의 노드 임베딩은 그래프의 로컬 정보와 글로벌 정보를 모두 반영하는 장점이 있다. 또한, 모든 노드 쌍이 아닌, 랜덤 워크에서 co-occurrence된 노드 쌍만을 사용하기 때문에 매우 효율적이다.
🏖️ 랜덤 워크 기반 임베딩 방법
랜덤 워크 기반 노드 임베딩을 구현하는 대표적인 알고리즘은 DeepWalk와 node2vec이다. 두 알고리즘은 랜덤 워크를 통해 노드 간의 관계를 모델링하고, 이를 기반으로 임베딩 벡터를 학습한다.
1. DeepWalk
DeepWalk는 그래프에서 랜덤 워크를 수행하여 노드의 시퀀스를 생성한 후, Skip-gram 모델을 이용해 노드 임베딩을 학습하는 알고리즘이다. 이는 텍스트 처리에서 사용되는 자연어 처리 기법을 그래프 데이터에 적용한 것이다.
예시
소셜 네트워크 그래프에서 DeepWalk를 사용하면, 사용자 간의 연결 관계를 반영한 임베딩 벡터를 얻을 수 있다. 이 벡터는 추천 시스템이나 링크 예측 등에서 사용될 수 있다.
<span style
="color:#1e90ff">2. node2vec
node2vec은 DeepWalk의 확장된 버전이다. DeepWalk에서는 랜덤 워크가 완전히 무작위로 이루어지지만, node2vec에서는 두 개의 파라미터 (p)와 (q)를 도입하여 랜덤 워크의 전략을 조절할 수 있다.
- p (Return Parameter):
이전에 방문한 노드로 돌아갈 확률을 조절한다. p값이 높을수록 이전 노드로 돌아갈 가능성이 낮아진다.
- q (In-out Parameter):
현재 노드와의 거리에 따라 다음 노드를 선택할 확률을 조절한다. q값이 높을수록 현재 노드와 가까운 노드를 선택할 가능성이 높다.
예시
학술 논문 인용 네트워크에서 node2vec을 적용하면, 논문 간의 인용 관계를 반영한 임베딩 벡터를 얻을 수 있다. 이를 통해 논문 추천, 인용 관계 예측 등의 작업을 수행할 수 있다.
🏖️ 정리
노드 임베딩은 그래프 상의 노드를 저차원 벡터로 변환하는 중요한 기법이다. 랜덤 워크 기반의 노드 임베딩은 그래프의 구조적 정보를 반영하여 효율적으로 노드 간의 유사성을 학습할 수 있다. 이를 통해 다양한 그래프 머신러닝 태스크에 활용할 수 있으며, DeepWalk와 node2vec은 이러한 임베딩 방법의 대표적인 알고리즘이다.
위와 같이 정리된 내용은 벨로그에 바로 적용할 수 있으며, 각 줄을 "이다", "있다"로 끝내어 가독성을 높였고, 요구하신 형식에 맞춰 색상 및 구분을 적용했습니다.
