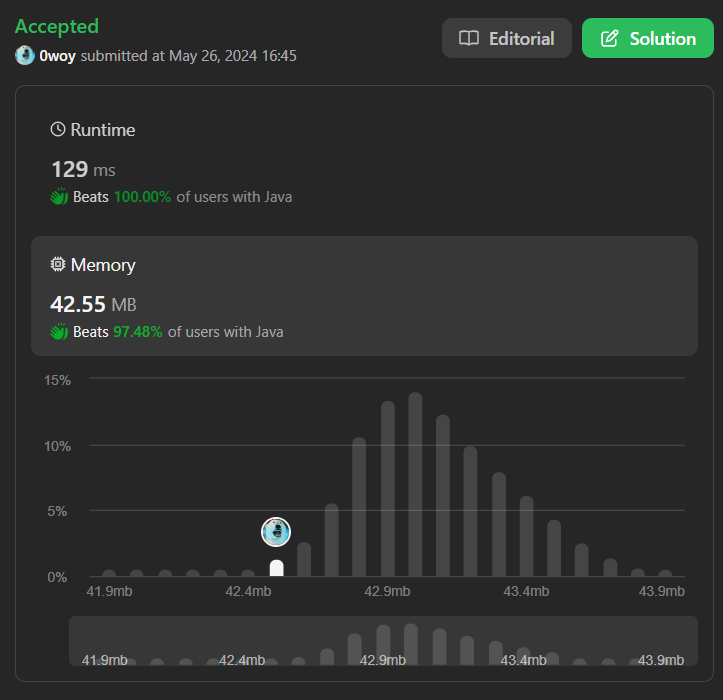
📜 문제
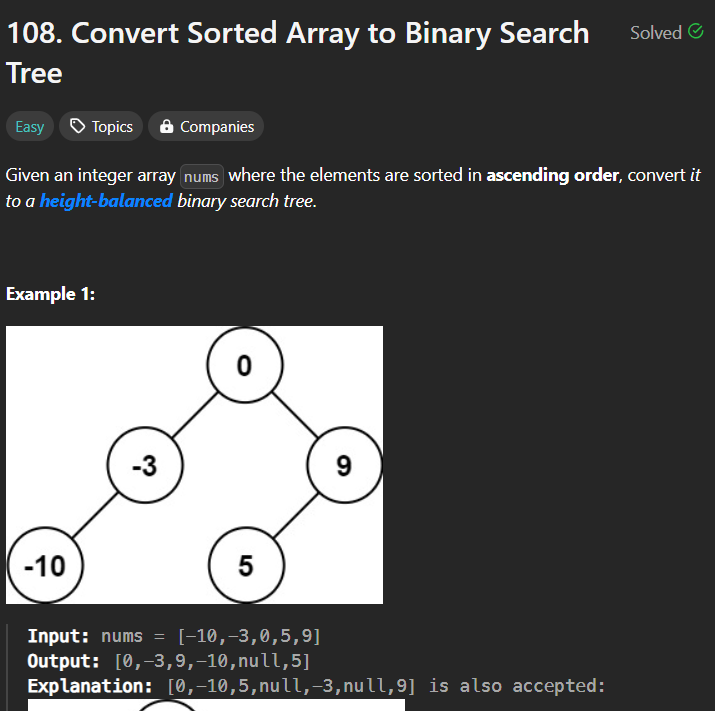
오름차순으로 정렬된 배열이 주어진다.
해당 배열을 height-balanced한 이진 트리로 변경하는 문제이다.
height-balanced?
모든 노드의 두 개의 서브트리의 깊이 차가 1을 초과하지 않아야 함.
보자마자 AVL 트리를 이용해 푸는 것 같은데,, 학부 때 상당히 귀찮았던 게 생각이 나서 다른 방법을 찾아보다가 그냥 AVL 트리를 만들어서 풀었다
❓ AVL Tree
이진 탐색 트리 중 하나로, 모든 노드의 균형을 유지하도록 설계된 자가 균형 이진 트리.
각 노드의 왼쪽 서브트리와 오른쪽 서브트리 높이 차이가 1을 넘지 않도록 유지함
최악의 경우에도 O(log n)의 시간 복잡로 삽입, 삭제 연산 수행
주요 개념
1. 균형 인수 (Balance Factor)
각 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이
-1, 0, 1값 중 하나로, 이 값을 벗어나면 균형을 잃은 것
- 회전 (Rotation)
트리가 균형을 잃을 때 트리 구조를 재조정하여 균형을 회복
LL, RR, LR, RL 회전
❓ 회전하는 경우
AVL 트리를 처음 본다면 회전하는 개념을 잘 모를 수 있다.
왜냐면 내가 학부 때 눈물 흘리면서 이해한 기억이 있기 때문..
(그래도 레드-블랙 트리에 비해 선녀였던 기억.....)
LL, RR, LR, RL 회전을 시행하는 경우를 그림으로 살펴보자
회전 이름은 균형이 깨진 노드를 기준으로 서브트리들의 위치를 통해 외웠다.
1. LL 회전
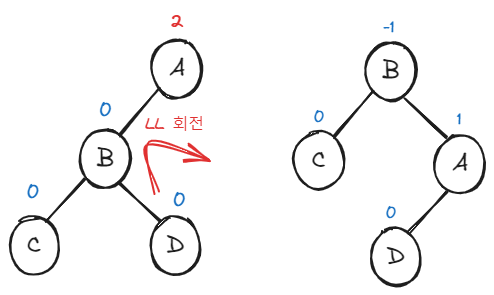
A 노드에서 높이 차가 2로 트리 재조정이 필요하다.
왼쪽 서브트리에 몰려서 LL 회전이라 외웠다.
D 삽입 전에 회전이 이루어져야 했지만,,
B가 양쪽 서브트리를 가진 채로 회전이 이루어 지는 과정을 보여주고 싶어서
이런 그림으로 준비해 봤습니다ㅎ
// LL 회전
public static TreeNode rotateRight(TreeNode parent){
TreeNode child = parent.left;
parent.left=child.right;
child.right = parent;
return child;
}오른쪽 방향으로 회전 하니까 함수 이름은 RotateRight 이다.
- parent 노드는 A이고, child 노드는 A의 왼쪽이므로 B이다.
- A의 왼쪽으로 B의 오른쪽 자식인 D를 이동해 주고,
- B의 오른쪽 자식으로 A를 지정해 준다.
LL 회전 끗!
2. RR 회전
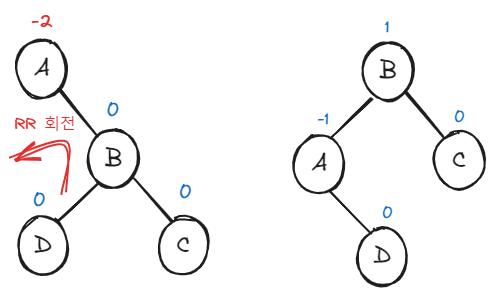
A 노드에서 높이 차가 -2로 트리 재조정이 필요하다.
이번엔 오른쪽 서브트리에 몰려 RR 회전이다 ㅎ
// RR 회전
public static TreeNode rotateLeft(TreeNode parent){
TreeNode child = parent.right;
parent.right=child.left;
child.left = parent;
return child;
}왼쪽 방향으로 회전 하니까 함수 이름은 RotateLeft 이다.
- parent 노드는 A이고, child 노드는 A의 오른쪽이므로 B이다.
- A의 오른쪽으로 B의 왼쪽 자식인 D를 이동해 주고,
- B의 왼쪽 자식으로 A를 지정해 준다.
RR 회전 끗!
3. LR 회전
요번에는 좀 복잡하다.
그래두 개안타. 그림으로 설명하면 쉽기 때문에..
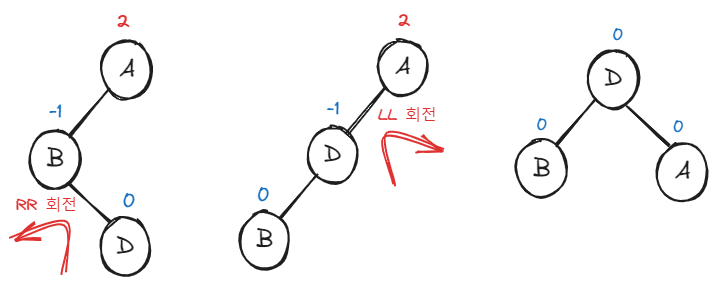
왼쪽, 오른쪽 순으로 노드가 있어서 균형을 잃었기 때문에 LR 회전이라고 외웠다.
먼저 B노드를 기준으로 RR 회전(RotateLeft)을 수행한다.
그 다음 LL 회전 설명할 때랑 똑같은 그림이 나온다.
이제 LL 회전을 갈겨주면 된다.
// LR 회전
if(balance>1 && key>node.left.val){
// RR 회전
node.left =rotateLeft(node.left);
// LL 회전
return rotateRight(node);
}회전이 2개가 이루어져서 복잡해 보이지만, 그림으로 보니까 쉽다! (가스라이팅)
4. RL 회전
LR 회전이랑 똑같다~
회전 순서가 반대일 뿐.
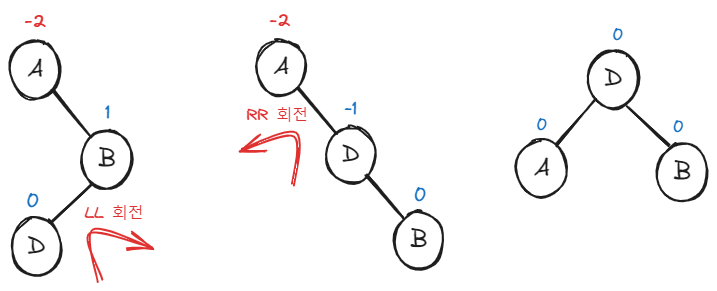
오른쪽, 왼쪽 순으로 노드가 있어서 균형을 잃었기 때문에 RL 회전이다.
먼저 B노드를 기준으로 LL 회전(RotateRight)을 수행한다.
그 다음엔 RR 회전을 갈겨준다.
// RL 회전
if(balance< -1 && key < node.right.val){
node.right = rotateRight(node.right);
return rotateLeft(node);
}요렇게 4가지 회전 하는 경우를 알아봤다.
✍ 부분 코드 설명
주어진 클래스
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution{
public TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = null;
for(int key : nums){
root = insert(root, key);
}
return root;
}
}반환 값이 TreeNode 이므로 root 노드를 생성 후, nums 배열 값을 차례대로 삽입한다.
삽입 함수 작성
public static TreeNode newNode(int key){
return new TreeNode(key);
}
public static TreeNode insert(TreeNode node, int key){
// node 생성 및 삽입
if(node==null) return newNode(key);
// key 값에 따라 단말노드까지 내려감
if(node.val > key){
node.left = insert(node.left, key);
}
else{
node.right = insert(node.right, key);
}
// 균형인수 확인
int balance = getBalance(node);
// RR 회전
if(balance>1 && key<node.left.val ){
return rotateRight(node);
}
// LL 회전
if(balance< -1 && key > node.right.val){
return rotateLeft(node);
}
// LR 회전
if(balance>1 && key>node.left.val){
node.left =rotateLeft(node.left);
return rotateRight(node);
}
// RL 회전
if(balance< -1 && key < node.right.val){
node.right = rotateRight(node.right);
return rotateLeft(node);
}
return node;
}- 삽입 시 key값에 맞게 단말 노드까지 내려간다.
- 노드를 삽입 후, 각 노드마다 균형인수를 확인한다.
- 균형을 잃었다면, 경우에 따른 회전을 진행한다.
- 갱신된 트리를 반환한다.
balance 는
왼쪽 서브트리 높이 - 오른쪽 서브트리 높이이다.
왼쪽 서브트리의 깊이가 오른쪽 보다 깊을 경우 양수,
오른쪽 서브트리가 더 깊은 경우 음수가 된다.
균형 인수 & 높이 구하기
// 높이 구하기
public static int getHeight(TreeNode node){
int height =0;
if (node == null) return 0;
// 왼쪽 서브트리, 오른쪽 서브트리 깊이 중 더 큰 값 + 1
height = 1+Math.max(getHeight(node.right), getHeight(node.left));
return height;
}
// 균형인수
public static int getBalance(TreeNode node){
// 노드가 비어있으면 0
if(node == null) return 0;
// 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
return getHeight(node.left)-getHeight(node.right);
}
회전
// LL 회전
public static TreeNode rotateRight(TreeNode parent){
TreeNode child = parent.left;
parent.left=child.right;
child.right = parent;
return child;
}
// RR 회전
public static TreeNode rotateLeft(TreeNode parent){
TreeNode child = parent.right;
parent.right=child.left;
child.left = parent;
return child;
}위에서 설명했으므로 패쓰!
🍳 전체 소스 코드
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public static TreeNode rotateRight(TreeNode parent){
TreeNode child = parent.left;
parent.left=child.right;
child.right = parent;
return child;
}
public static TreeNode rotateLeft(TreeNode parent){
TreeNode child = parent.right;
parent.right=child.left;
child.left = parent;
return child;
}
public static int getHeight(TreeNode node){
int height =0;
if (node == null) return 0;
height = 1+Math.max(getHeight(node.right), getHeight(node.left));
return height;
}
public static int getBalance(TreeNode node){
if(node == null) return 0;
return getHeight(node.left)-getHeight(node.right);
}
public static TreeNode newNode(int key){
return new TreeNode(key);
}
public static TreeNode insert(TreeNode node, int key){
if(node==null) return newNode(key);
if(node.val > key){
node.left = insert(node.left, key);
}
else{
node.right = insert(node.right, key);
}
int balance = getBalance(node);
// RR 회전
if(balance>1 && key<node.left.val ){
return rotateRight(node);
}
if(balance< -1 && key > node.right.val){
return rotateLeft(node);
}
// LR 회전
if(balance>1 && key>node.left.val){
node.left =rotateLeft(node.left);
return rotateRight(node);
}
if(balance< -1 && key < node.right.val){
node.right = rotateRight(node.right);
return rotateLeft(node);
}
return node;
}
public TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = null;
for(int key : nums){
root = insert(root, key);
}
return root;
}
}✨ 결과
AVL 트리는 오랜만인데, 재밌었다!