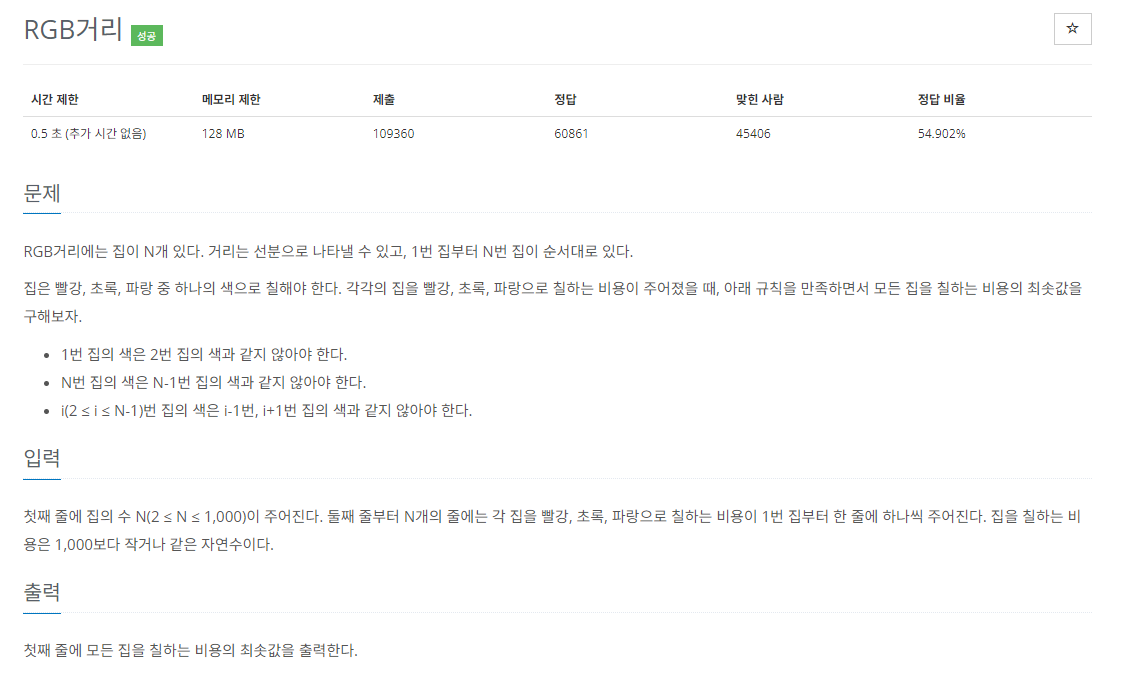
📜 문제
- N개의 집에 서로 이웃한 집과는 다른 색으로 칠함
- 각 줄 번호에 해당하는 집을 R G B 값으로 칠하는 비용이 주어짐
- 모든 집을 칠하는 최소 비용 구하기
현재 줄에서 최솟값만 취하면 되는 것 같지만, 그렇지 않다.
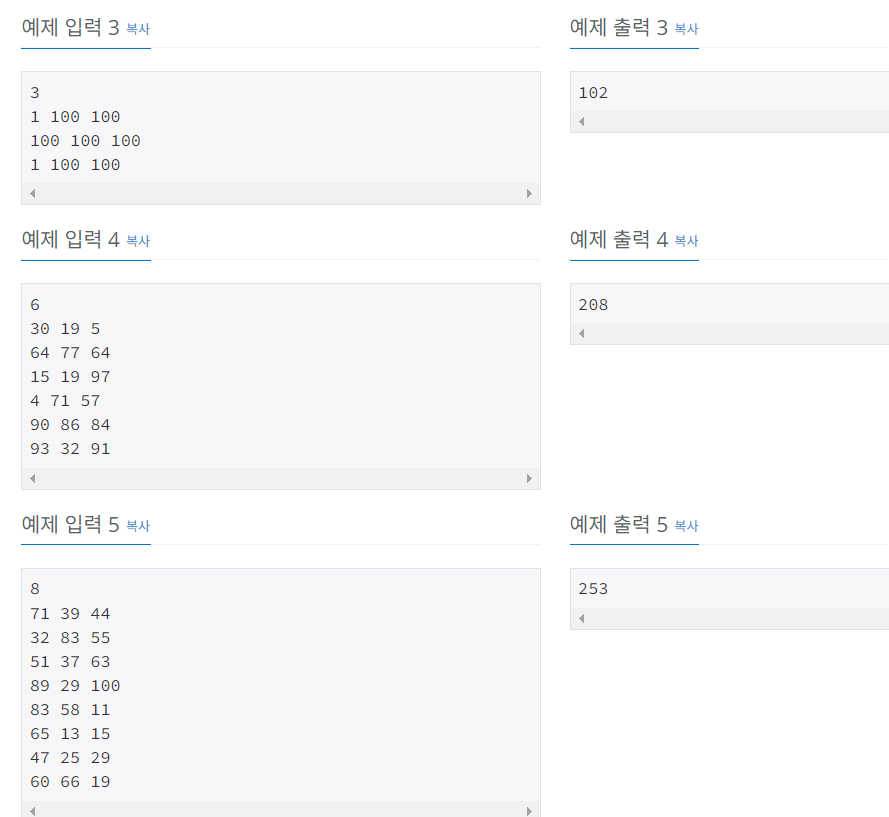
예제 5의 경우를 살펴보자.
| R | G | B |
|---|---|---|
| 71 | 39 | 44 |
| 32 | 83 | 55 |
| 51 | 37 | 63 |
| 89 | 29 | 100 |
| 83 | 56 | 11 |
| 65 | 13 | 15 |
| 47 | 25 | 29 |
| 69 | 66 | 19 |
최소값만 취하는 경우, 39+32+37+89+11+13+29+66 = 316이 된다.
하지만, 답은 39+32+63+29+11+13+47+19=253 이다.
그래서 나는 모든 경우의 수를 더하는 방법을 택했다.
- 모든 집을 칠하는 비용을 담은 2차원 배열 rgb를 만든다.
- n까지의 집을 칠하는 경우 최소값을 담을 2차원 배열 dp를 만든다.
- i번째 집을 R로 칠하는 경우의 최소값, G로 칠하는 경우 최솟값, B로 칠하는 경우의 최솟값을 갱신해 나간다.
즉, i번째 집을 R로 칠하는 경우는
dp[i][0] = rgb[i][0]+(dp[i-1][1], dp[i-1][2] 중 더 작은 값)이 된다.B, G로 칠하는 경우도 위와 동일하다.
ex) n=3
RGB 비용 테이블
| n | R | G | B |
|---|---|---|---|
| 1 | 71 | 39 | 44 |
| 2 | 32 | 83 | 55 |
| 3 | 51 | 37 | 63 |
DP 테이블
| n | R | G | B |
|---|---|---|---|
| 1 | 71 | 39 | 44 |
| 2 | 32+39=71 | 83+44=127 | 55+39=94 |
| 3 | 51+94=145 | 37+71=108 | 63+71=134 |
n이 3인 경우 G R G 순으로 칠한 108이 답이된다.
✍ 부분 코드 설명
점화식을 통해 최소 연산 횟수 구하기
dp[0][0] = rgb[0][0];
dp[0][1] = rgb[0][1];
dp[0][2] = rgb[0][2];
for(int i=1;i<n;i++){
for(int j=0;j<3;j++){
dp[i][j] =
rgb[i][j]+Math.min(dp[i-1][(j+1)%3], dp[i-1][(j+2)%3]);
}
}점화식을 이용해 dp 배열에 값을 저장한다.
최소 비용 구하기
int min = (dp[n-1][0]>dp[n-1][1])
?(dp[n-1][1]>dp[n-1][2]?dp[n-1][2]:dp[n-1][1])
:(dp[n-1][0]>dp[n-1][2]?dp[n-1][2]:dp[n-1][0]);
System.out.println(min);연산 과정을 통해 도출한 n번째 집까지 칠했을 때 가장 최솟값을 구한 후 출력한다.
🍳 전체 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int [][] dp = new int[n][3];
int [][] rgb = new int [n][3];
for(int i=0;i<n;i++){
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j=0;j<3;j++){
rgb[i][j] = Integer.parseInt(st.nextToken());
}
}
dp[0][0] = rgb[0][0];
dp[0][1] = rgb[0][1];
dp[0][2] = rgb[0][2];
for(int i=1;i<n;i++){
for(int j=0;j<3;j++){
dp[i][j] = rgb[i][j]+Math.min(dp[i-1][(j+1)%3], dp[i-1][(j+2)%3]);
}
}
int min = (dp[n-1][0]>dp[n-1][1])
?(dp[n-1][1]>dp[n-1][2]?dp[n-1][2]:dp[n-1][1])
:(dp[n-1][0]>dp[n-1][2]?dp[n-1][2]:dp[n-1][0]);
System.out.println(min);
}
}
✨ 결과
머리에서 생각나는 대로 점화식을 세우고 코드를 짜봤는데 이게 되네? 라는 생각이 들었다.
시간 제한이 0.5초라서 시간 초과 메세지가 뜰 줄 알았는데 정말 이게 됐다.
문제 풀이 과정을 작성할 때마다 다른 사람이 어떻게 해야 이해할 수 있을지 고민하면서 최대한 쉽게 작성하려고 노력하는데 잘 전달 됐으면 좋겠다.