📜 문제
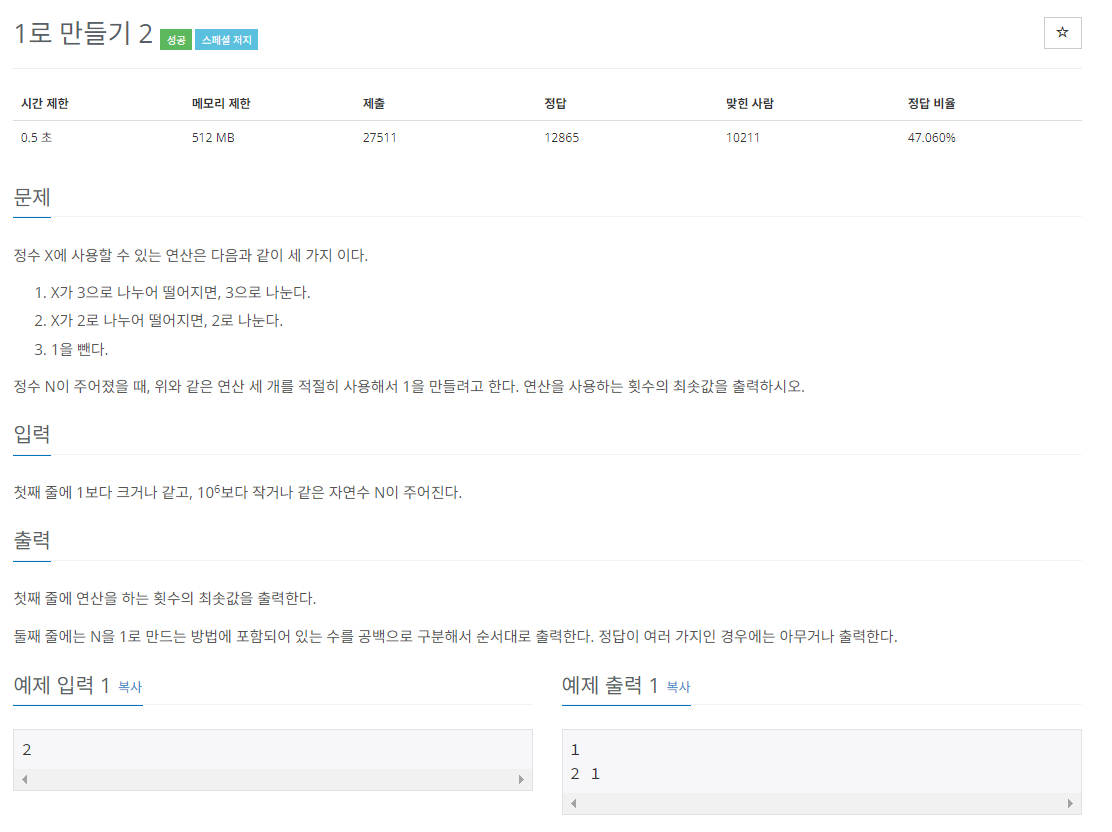
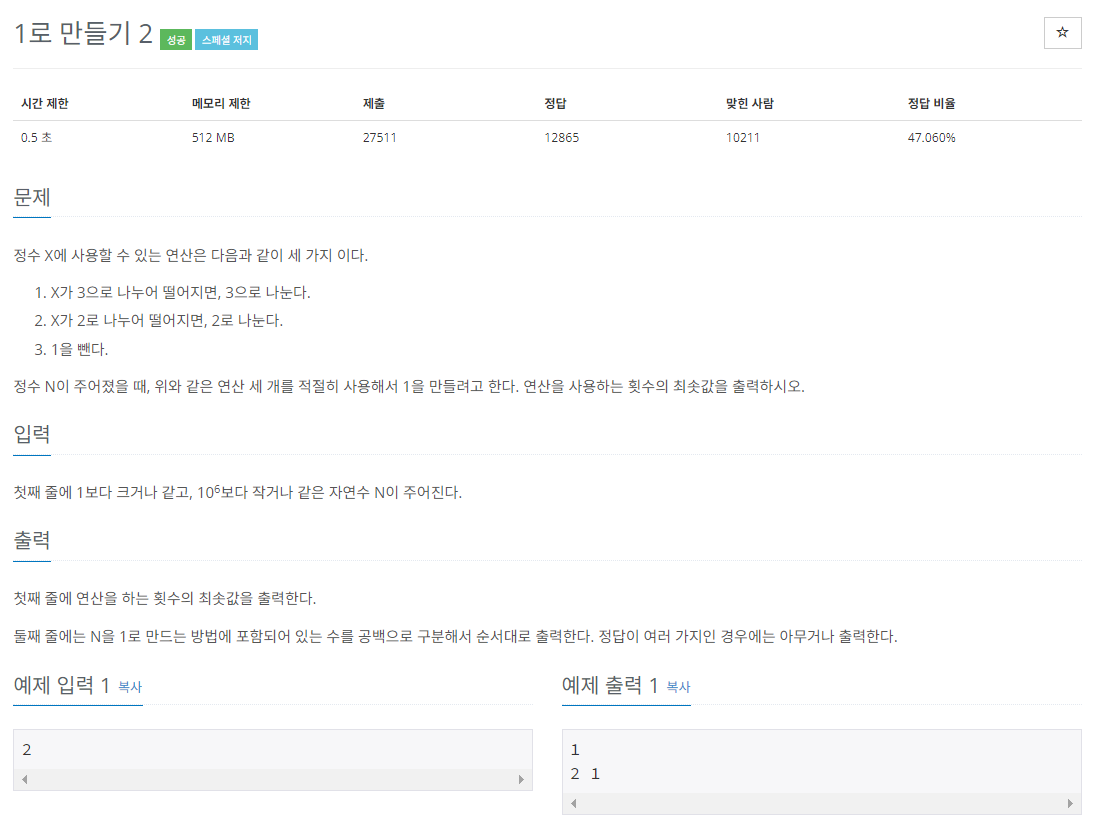
- 숫자 X를 입력 받고, 아래의 3가지 방법을 사용해 1로 만드는 연산의 최소 횟수 및 과정 출력.
방법
- 숫자가 3으로 나누어 떨어지면 3으로 나눔
- 숫자가 2로 나누어 떨어지면 2로 나눔
- 숫자에서 1을 뺌
숫자 X를 1로 만드는 과정을 10까지 만들어 보자
| 숫자 | 최소 연산 횟수 | 과정 |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 1 | 2 1 |
| 3 | 1 | 3 1 |
| 4 | 2 | 4 3 1 / 4 2 1 |
| 5 | 3 | 5 4 3 1 / 5 4 2 1 |
| 6 | 2 | 6 3 1 / 6 2 1 |
| 7 | 3 | 7 6 3 1 / 7 6 2 1 |
| 8 | 3 | 8 4 2 1 |
| 9 | 2 | 9 3 1 |
| 10 | 3 | 10 9 3 1 |
X는 3으로 나누어지는 수, 2로 나누어 떨어지는 수, 2와 3 모두 나누어 떨어지는 수, 2와 3 모두 나누어 떨어지지 않는 수 로 총 4가지 경우가 있다.
1) 2로 나누어 떨어지는 경우
EX) X = 8
8의 연산과정은8 4 2 1로 총 3번의 연산이 수행된다.
그런데,4 2 1연산은 X가 4인 경우의 연산과정과 동일하다.
즉, 최소 연산 횟수는dp[8] = dp[8/2]+1로 식을 세울 수 있다.EX) X = 4
그런데, 4의 경우 연산 과정이4 3 1또는4 2 1로 두 개가 나온다.
4 2 1연산의 경우 8의 예시와 동일한 방식이지만,4 3 1의 경우는 4가 3보다 +1이 크기때문에 3의 연산에서 1을 더한 값과 같다.
즉,dp[4] = dp[4-1]+1로도 식을 세울 수 있다.
2) 3으로 나누어 떨어지는 경우
EX) X = 9
9의 연산과정은9 3 1로 총 2번의 연산이 수행된다.
2로 나누어 떨어지는 식과 같이dp[9] = dp[9/3]+1로 최소 연산 횟수 식을 세울 수 있다.1) 과 마찬가지로 8의 연산과정에서 +1한 값이 9가 되므로,
dp[9] = dp[9-1]+1의 식도 세울 수 있다.
3) 2와 3 모두 나누어 떨어지는 경우
X가 2와 3 모두 나누어 떨어지는 경우는 1) 과 2) 두 가지 방법을 모두 사용할 수 있다.
dp[X/2]+1또는dp[X/3]+1값 중 더 작은 값을 취하면 된다.
4) 2와 3 모두 나누어 떨어지지 않는 경우
모두 나누어 떨어지지 않는 경우는 1을 빼는 연산만 사용할 수 있으므로,
dp[x] = dp[x-1]+1 의 식이 성립된다.
이미 dp[x-1]의 최소 연산 횟수는 구해져 있음.
✍ 부분 코드 설명
점화식을 통해 최소 연산 횟수 구하기
dp[1] =0;
dp[2] =1;
dp[3] =1;
for(int i=4;i<=n;i++){
int tmp = Integer.MAX_VALUE;
if(i%2==0) tmp = Math.min(dp[i/2], tmp);
if(i%3==0) tmp = Math.min(dp[i/3], tmp);
tmp = Math.min(dp[i-1],tmp);
dp[i] = tmp+1;
}
sb.append(dp[n]+"\n");dp 배열은 각 인덱스가 되는 숫자의 최소 연산 횟수를 저장하는 배열이다.
1, 2, 3의 경우 미리 초기화 한다.
a. tmp 변수를 선언하고 초기화 한다.
b. 2로 나누어 떨어지는 경우 dp[i/2]와 tmp 값 중 더 작은 값을 tmp에 저장한다.
c. 3으로 나누어 떨어지는 경우 dp[i/3]과 tmp 값 중 더 작은 값을 tmp에 저장한다.
d. 이전 값(dp[i-1]) tmp 값 중 더 작은 값을 tmp에 저장한다.
위 과정은 조건에 따라 tmp 값을 갱신 하면서 결과적으로 최소 연산 횟수를 구한다.
연산 과정 구하기
while (true){
sb.append(n+" ");
int tmp = Integer.MAX_VALUE;
int idx=-1;
if(n==1) break;
if(n%2==0){
if(dp[n/2]<tmp){
tmp = dp[n/2];
idx = n/2;
}
}
if(n%3==0){
if(dp[n/3]<tmp){
tmp = dp[n/3];
idx =n/3;
}
}
if(dp[n-1]<tmp) idx =n-1;
n = idx;
}연산 과정을 구하기 위한 코드이다.
- n이 1인 경우 연산이 종료되므로 반복문을 빠져 나간다.
- 최소 연산 횟수를 구하는 조건식과 동일하지만, idx 값이 연산 과정이 된다.
- 반복문 처음에 n 값을 sb에 저장한다.
🍳 전체 소스 코드
package Algorithm.DP;
import org.w3c.dom.ls.LSOutput;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class N_12852 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
int [] dp = new int [n+3];
dp[1] =0;
dp[2] =1;
dp[3]=1;
for(int i=4;i<=n;i++){
int tmp = Integer.MAX_VALUE;
if(i%2==0) tmp = Math.min(dp[i/2], tmp);
if(i%3==0) tmp = Math.min(dp[i/3], tmp);
tmp = Math.min(dp[i-1],tmp);
dp[i] = tmp+1;
}
sb.append(dp[n]+"\n");
while (true){
sb.append(n+" ");
int tmp = Integer.MAX_VALUE;
int idx=-1;
if(n==1) break;
if(n%2==0){
if(dp[n/2]<tmp){
tmp = dp[n/2];
idx = n/2;
}
}
if(n%3==0){
if(dp[n/3]<tmp){
tmp = dp[n/3];
idx =n/3;
}
}
if(dp[n-1]<tmp) idx =n-1;
n = idx;
}
System.out.println(sb);
}
}
✨ 결과
가장 최근 결과가 설명한 코드로 문제를 푼 결과이다.
두 번째 결과를 보면 메모리와 시간을 상당히 잡아 먹었는데, 이에 충격 먹고 다른 분의 코드를 참고 후 이해하여 정리해서 올렸다.
연산 횟수를 구하는 점화식을 도출하는 건 어렵지 않았는데 바보같이 연산 과정을 구하는 일을 많이 돌아갔다...
그래도 뿌듯한 점은 실버 1 문제를 풀었다는 것이다..
엊그제만 해도 실버 3도 많이 슬펐는데 뇌가 말랑말랑 해졌나 보다 히히.
🍰 비효율 코드
조건식 하나하나 작성하기
시간과 메모리를 많이 잡아 먹은 코드는 조건식을 하나하나 작성했다. 다시 봐도 왜 이렇게 풀었는지 모르겠다. 많이 힘들었나,,,,
switch (n){
case 1:
dp[1] =0;
sol[1]= "1";
break;
case 2:
dp[2]=1;
sol[2]="1 2";
break;
case 3:
dp[3]=1;
sol[3] ="1 3";
break;
}
if(n>3) {
dp[1] =0;
sol[1]= "1";
dp[2] =1;
sol[2]="1 2";
dp[3] =1;
sol[3] ="1 3";
for (int i = 4; i <= n; i++) {
if(i%3==0&&i%2!=0) {
if(dp[i/3]<dp[i-1]){
dp[i] = dp[i/3]+1;
sol[i] = sol[i/3]+" "+i;
}
else{
dp[i]=dp[i-1]+1;
sol[i]=sol[i-1]+" "+i;
}
}
else if(i%3==0&&i%2==0){
if(dp[i/3]<dp[i/2]){
dp[i] = dp[i/3]+1;
sol[i] = sol[i/3]+" "+i;
}
else{
dp[i]=dp[i/2]+1;
sol[i]=sol[i/2]+" "+i;
}
}
else if(i%2==0){
if(dp[i/2]<dp[i-1]){
dp[i] = dp[i/2]+1;
sol[i] = sol[i/2]+" "+i;
}
else{
dp[i]=dp[i-1]+1;
sol[i]=sol[i-1]+" "+i;
}
}
else{
dp[i]=dp[i-1]+1;
sol[i] = sol[i-1]+" "+i;
}
}
}
세상에서 가장 비효율적인 조건식이다.
내 문제가 여기서 드러나는데, else if가 없으면 세상이 무너진다고 생각한다.
그리고 반복문 하나로 모든 걸 끝내려고 한다.
본문에서 설명한 코드처럼 if만 사용해도 모든 조건식을 깔끔하게 확인할 수 있는데, 막상 조건을 따져야 하는 문제만 보면 하나하나 조건을 만들어준다.
연산과정 구한다고 String 배열 선언한 것도 상당히 괴랄하다.
급할 수록 돌아가라고 하지만 적당히 돌아가야지 나처럼 너무 돌아가면 안 된다