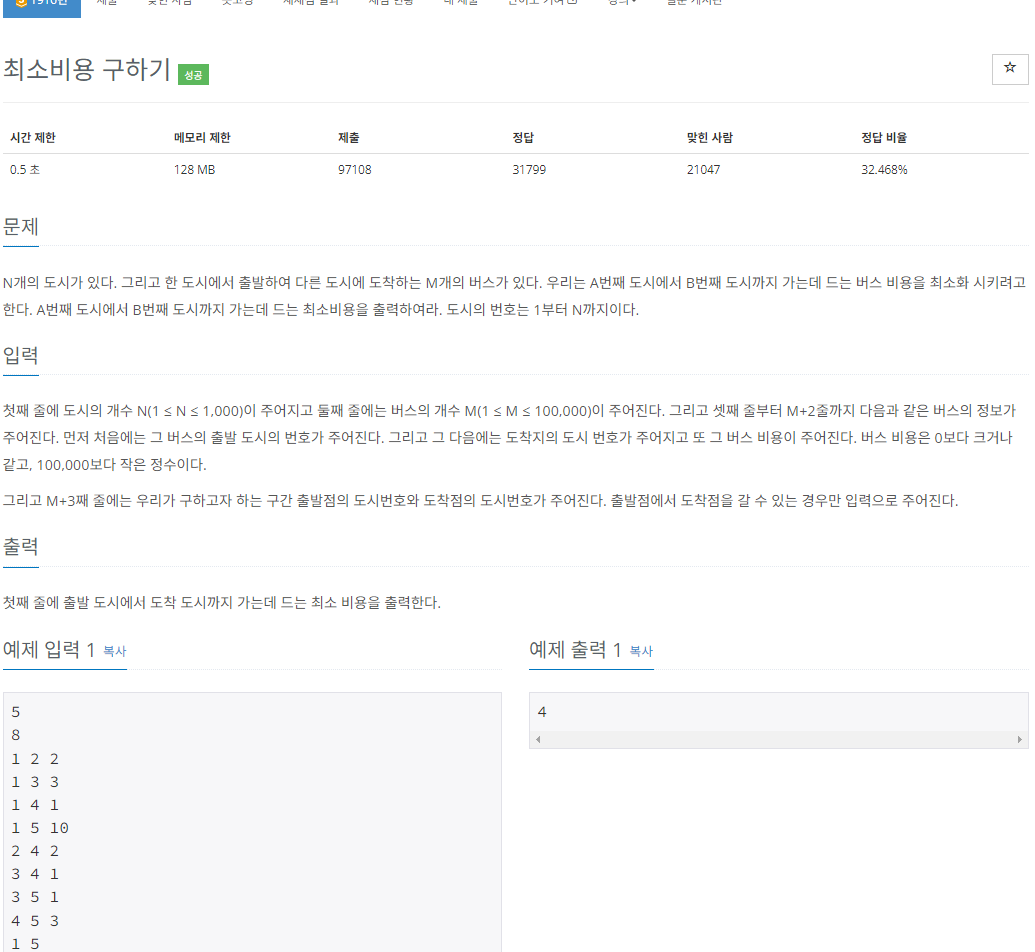
문제사항

골드 5단계 문제였다.

앞서 풀었던 [백준] 1753번 최단경로(JAVA)와 동일하게 다익스트라 알고리즘을 사용한 문제였다.

다익스트라 알고리즘에 대해 궁금하다면 위 포스팅을 참고하자.

사실 최단경로 문제는 최단거리 배열을 모두 출력하는 것이라면, 해당 문제는 출발 도시에서 도착 도시까지 가는데 드는 최소 비용을 구하는 것이므로 마지막 도착노드의 최소 비용(최단거리) 값을 출력하면 되기 때문에 유형은 똑같다고 볼 수 있다.

최단경로 문제를 풀 때는 방문 배열을 만들어서 노드의 방문 여부를 명시적으로 체크하였으나 이를 제외해도 충분히 코드 구현이 가능한 문제임을 깨달았다.

되려 방문 배열을 만들면 시간 초과가 뜬다는 것을 깨닫고, 방문 배열을 제거하고 D 배열만으로 방문 여부를 판단하였다.

이미 우선순위 큐에 최단거리 값을 가중치 값으로 넣어주기 때문에 충분히 판단이 가능한 것이다.

알고리즘 분류

그래프 (다익스트라)

코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());
        int M = Integer.parseInt(br.readLine());

        //인접 리스트
        ArrayList<Node>[] grape = new ArrayList[N + 1];
        //최단거리 배열
        int[] D = new int[N + 1];

        for (int i = 0; i <= N; i++) {
            grape[i] = new ArrayList<>();
            D[i] = Integer.MAX_VALUE;
        }

        StringTokenizer st;
        for (int i = 1; i <= M; i++) {
            st = new StringTokenizer(br.readLine());
            int A = Integer.parseInt(st.nextToken());
            int B = Integer.parseInt(st.nextToken());
            int C = Integer.parseInt(st.nextToken());
            grape[A].add(new Node(B, C));
        }

        st = new StringTokenizer(br.readLine());
        int start = Integer.parseInt(st.nextToken());
        int end = Integer.parseInt(st.nextToken());

        //다익스트라 -> 우선순위 큐
        PriorityQueue<Node> que = new PriorityQueue<>();
        //출발 도시 최단거리 0
        D[start] = 0;
        que.offer(new Node(start, 0));

        while (!que.isEmpty()) {
            Node now = que.poll();

            if (now.e > D[now.toNode]) continue;  // 이미 더 짧은 경로를 찾았다면 스킵

            for (Node next : grape[now.toNode]) {
                int newCost = D[now.toNode] + next.e;
                if (newCost < D[next.toNode]) {
                    D[next.toNode] = newCost;
                    que.offer(new Node(next.toNode, newCost)); //이미 우선순위 큐에 최단거리 값을 가중치 값으로 넣어주기 때문에 중복 검증 피할 수 있음
                }
            }
        }
        System.out.println(D[end]);
    }

    static class Node implements Comparable<Node> {
        int toNode;
        int e;
        @Override
        public int compareTo(Node node) { //가중치 비교 (작은 값)
            return this.e - node.e;
        }

        public Node(int toNode, int e) {
            this.toNode = toNode;
            this.e = e;
        }
    }
}