1. What is Logistic Regression

why) 왜 배우냐면용
→ Neural Net의 한 단위인 Neuron에서 Logistic Regression (이하 Log. R)이 사용됨.

▶️ use) Binary Classification에서 활용될 수 있다.
▶️ use) 곡선 형태의 함수가 필요한 경우 (즉 Lin. R 적용이 어려운 경우) Log. R을 사용한다.

Binary Classification(이진 분류)을 위해 neuron 하나에서 사용되는 모델

Linear R vs Log. R

Lin. R → 편평한 평면
Log. R → Lin. R에 sigmoid func.을 적용하여 S자로 굽어 있는 hyperplane을 모델링

2. How to do Logistic Regression

goal) Parameter인 W와 b를 $\hat{y}$이 ground truth (y) 에 가까워지도록 학습한다.

1) Forward Propagation

추청값 ($\hat y$)를 도출한다.

• Input: $\{(x^{(1)}, y^{(1)}), ... (x^{(m)},y^{(m)}) \}$ → training data m개
• Model: $\hat{y}=\sigma(w^Tx+b)$
  • Input: $x$
  • Parameter: $w, b$ (w: weight, b: bias)
  • Activation Function: $\sigma$
  • Output: $\hat{y}$

*Log. R = a(Lin. R) (Lin. R에 sigmoid function을 적용한 것)

2) Backward Propagation

Cost가 작아지도록, $W, b$를 gradient descent를 통해 조절한다.

2-1) Cost function

델타값 ($y - \hat{y}$)을 표현하는 함수

1) Loss function

• Sum of Squared Error $\frac{1}{2} (\hat y - y)^2$
  고전 ANN에서 loss를 정의하는 방법
  🥲 pb) non-convex, 多 local optima

• Cross-Entropy Loss $-(ylog\hat y +(1-y)log(1-\hat y))$

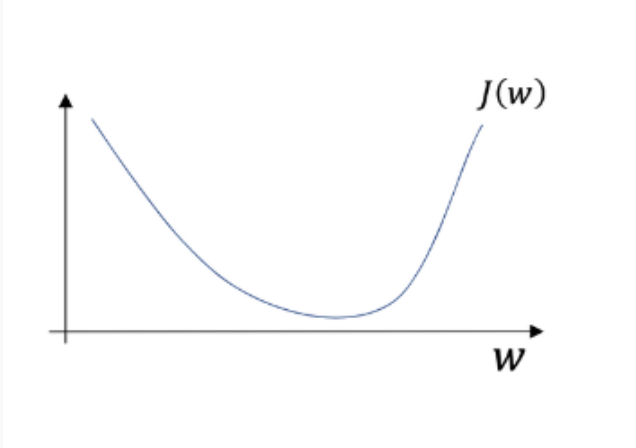
  Deep NN에서 사용되는 방법
  👍🏻 일반적으로 다른 손실 함수보다 높은 성능을 보인다.

  👍🏻 미분 가능하므로 Gradient Descent 사용이 가능하다.
  $L$ 이 0이 되는 것
  == 엔트로피의 기댓값이 최소화 되는 것
  == 추정값이 ground truth에 가까워지는 것

2) Cost function: 각 training data 들의 Loss의 평균

$J(w,b) = \frac{1}{m} \sum L(\hat y ^{(i)}, y^{(i)})$

2-2) Gradient Descent (경사 하강법)

cost function (J) 을 최소화하는 parameter를 찾기 위한 알고리즘

how) to do G.D
1. 초기 w 설정
2. gradient 계산
3. descent하는 방향으로 w 업데이트
4. convergence까지 반복

구현은 다음과 같다.
Repeat {
$w$ ← $w - \alpha \frac{dJ(w,b)}{dw}$
$b$ ← $b - \alpha \frac{dJ(w,b)}{db}$
}