1 Hierarchical Method

---

☑️ what) 종결 조건을 만족할 때까지 데이터를 나눈다.
cf) Partitioning Method(K-Means, K-Medoids...)는 몇 개로 나눌지 ($K$)에 대한 조건이 필요한 반면, 계층적 방법은 종결 조건을 필요로 한다.

1. AGNES, DIANA

계층적 클러스터링 방법으로 다음의 2가지가 있다.

	AGNES ; Bottom-Up Approach	DIANA ; Top-Down Approach
	AGglomerative NESting (계층적 군집화)	DIvisive ANAlysis
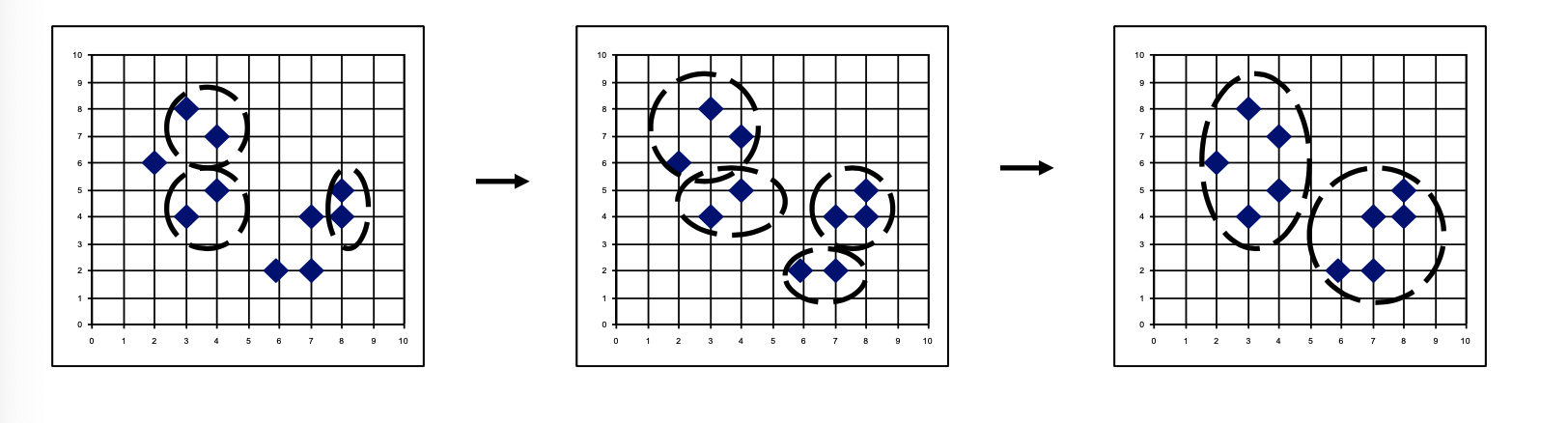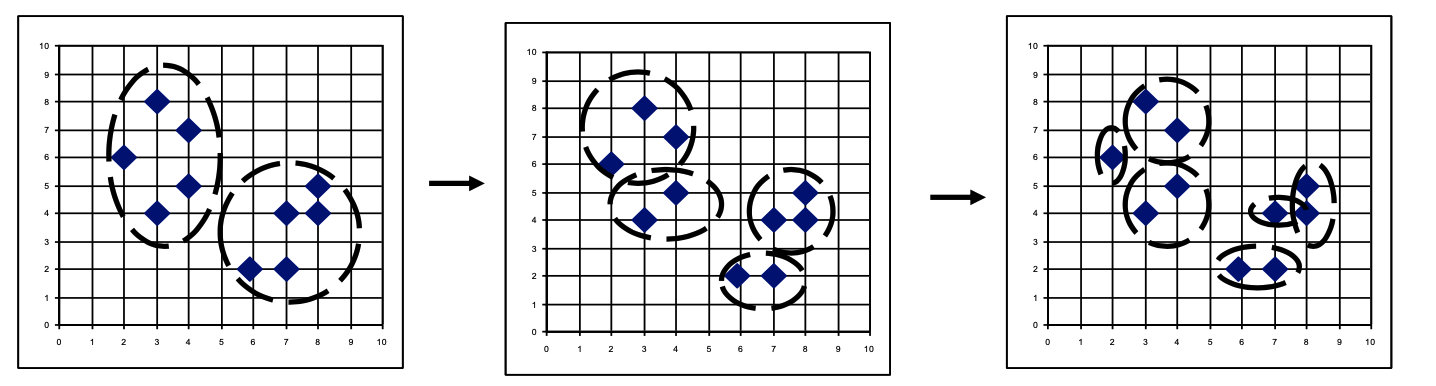Algorithm	i) single-link method로 클러스터 간 거리를 측정한다. ii) 가장 가까운 클러스터를 합친다. iii) 최종적으로 하나의 클러스가 된다. iv) Dendrogram에서 원하는 레벨을 고른다.	i) 가장 큰 클러스터를 2개 클러스터로 나눈다. ii) 최종적으로 모든 클러스터가 하나의 데이터를 포함한다.
1st step Complexity	$_nC_2 = \frac {n(n-1)}{2}$ : n개 중 2가지를 합쳐야 함	$2^{n-1} -1$ : n개의 데이터가 2개 클러스터 중 하나를 선택해야 함. -> sol) approximation 알고리즘 필요

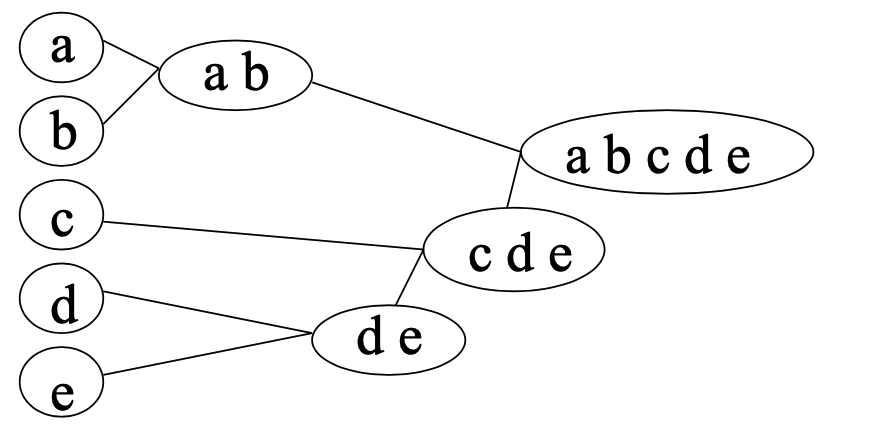
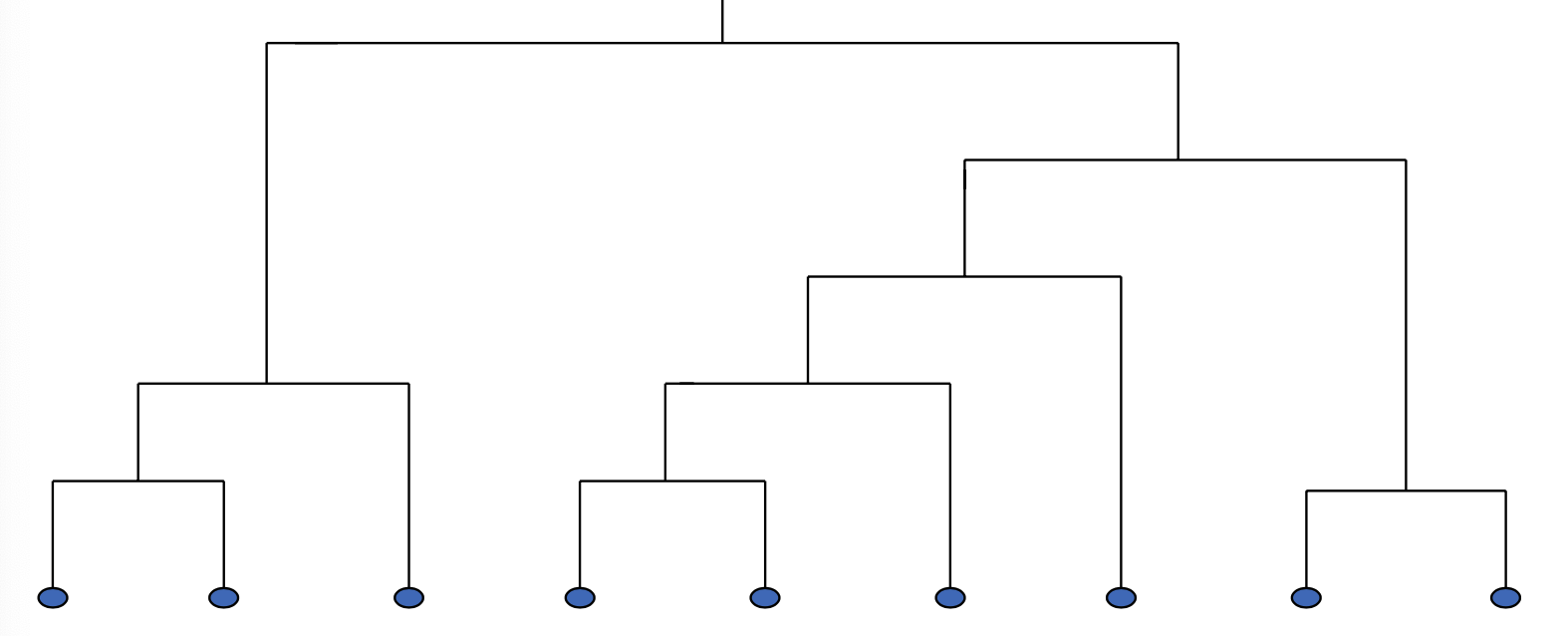
1) Dendrogram

☑️ what) 계층적으로 나누어진 여러 레벨의 클러스터 결과를 분해한 트리 모형의 그래프

2 Advanced Hierarchical Method (Distance + Hierarchical)

---

🥲 pb) 계층 클러스터링은 시간 복잡도가 $O(n^2)$로, 스케일이 어렵다.
→ sol) 거리 기반 클러스팅을 통합한 계층 모델 $\ni$ BIRCH, ROCK, CHAMELEON

1. BIRCH

Balanced Iterative Reducing and Clutering using Hierarchies

☑️ what) CF tree를 사용하여 계층적으로 클러스터링을 수행한다.

👍🏻 gd) Scales Linearly: 한 번의 DB 스캔 만으로 좋은 클러스터링을 찾을 수 있다.
🥲 pb) 숫자 데이터에만 적용 가능, 데이터의 순서에 영향을 받는다. (같은 데이터라도 순서에 따라 결과가 달라 可 )

how) algorithm
i) scan DB
ii) leaf 노드부터 클러스터링 알고리즘 적용. (옵션: refine the result)

1) CF (Clustering Feature)

☑️ what)	▶️ use)	👍🏻 gd)
주어진 클러스터의 통계 요약. (compact representation of data) $CF = (n, \vec {LS}, \vec {SS})$ $n$ : 클러스터의 데이터 개수 $LS$ : Linear Sum $SS$ : Square Sum	- centroid = $\frac {\vec {LS}}{n}$ - Radius - Diameter	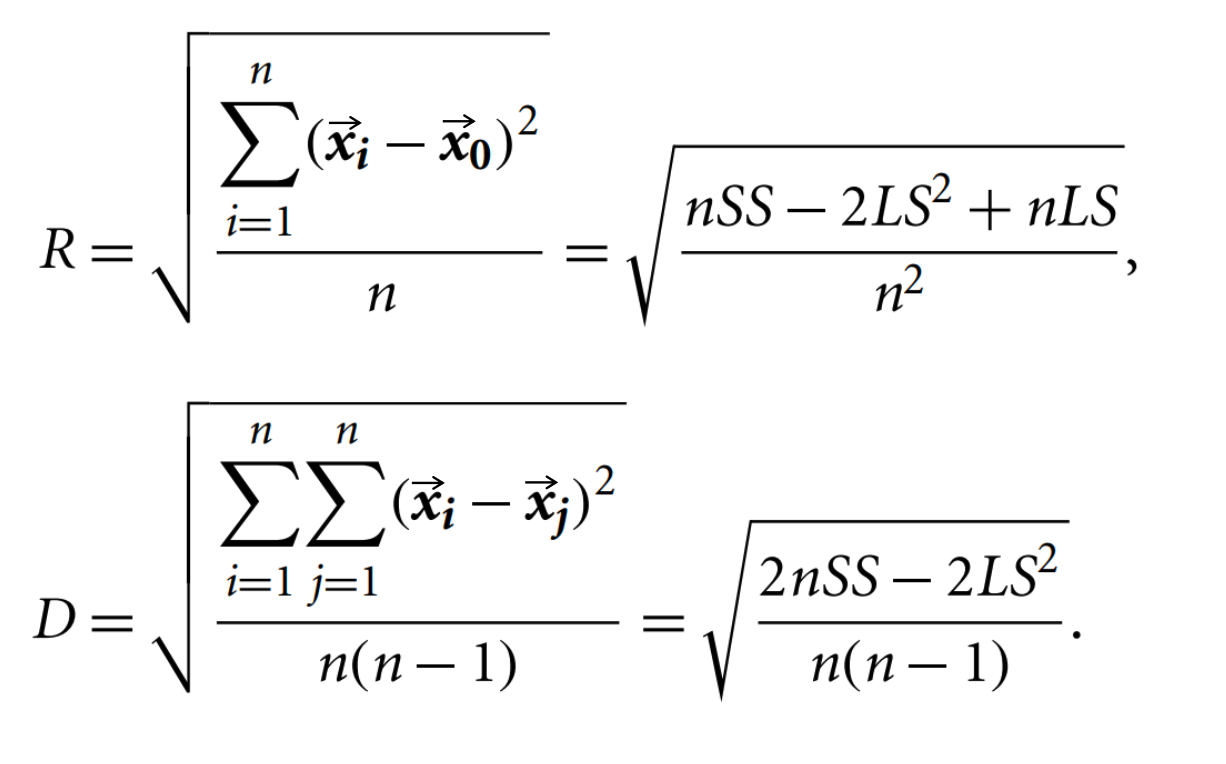radius, diameter를 쉽게 알 수 있다. Radius: avg(centroid와 포인트들의 거리) Diameter: avg(모든 페어 거리)

2) CF-Tree

☑️ what) height-balanced tree $\ni$ 계층적 클러스터링을 위한 CF

• Leaf Node $\ni$ sub-clusters + their CF
• Non-Leaf Node $\ni$ sum of CF of its children

• 실제 데이터가 포함되어 있지 않음에 주의. 그저 CF로 표방되는 메타데이터만 들어있다.
  → 👍🏻 gd) compact 하면서 계층적인 구조의 데이터 표현을 얻을 수 있다.
• Hyper-parameter of CF-tree
  • B, L (Branching Factor) ; 자식 노드의 최대 숫자 특정
    • L: max num of leaf
    • B: max num of non-leaf node
  • Threshold ; max radius (or diameter) of a cluster
    • cluster를 포함하는 leaf에만 적용된다.
    • cluster가 threshold 넘는 값을 가지면 splitted

2. CHAMELEON

☑️ what) 클러스터 간 유사성과 클러스터 내부 유사성이 모두 높은 두 클러스터를 병합한다.
👍🏻 gd) 크기와 모양이 다양하다.

how) algorithm
i) KNN graph를 그린다.
ii) Partition: KNN 그래프를 서브 클러스터로 분해한다.
iii) Merge: 서브 클러스터를 결합한다.

1) Partition

edge-cut (잘린 edge weight의 합)이 최소가 되도록 분해한다.
hMeTis library (METIS)가 사용된다.

2) Merging

다음의 기준에 따라 병합한다.

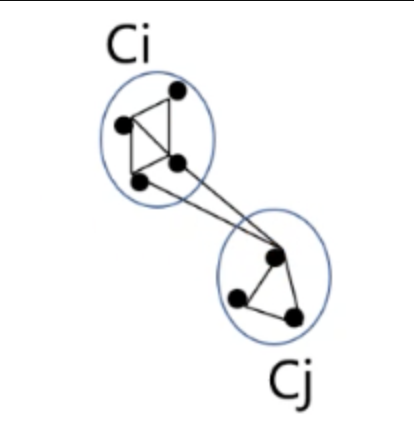
다음의 2가지를 고려한다.
1. RI: Relative Inter-Connectivity

e.g. $\frac {2}{\frac 1 2 (3 + 2)} = 0.8$
2. Relative Closeness