[Data Science] Clustering (2) Partitioning Method; K-Means, PAM(K-Medoids), K-modes, CLARA
강의-데이터사이언스
목록 보기
6/9
0 Partitioning Method
☑️ what) N개의 데이터를 K개의 클러스터로 나눈다.
클러스터의 representative (e.g. centroid, medoid)를 정하고, 다음 식의 클러스터별 총합이 최소가 되도록 나눈다.
🥲 pb) 가 hyper-parameter이다, non-convex 모양의 클러스터는 찾을 수 없다.
where
: the number of clusters (pre-defined)
: the number of data points in the m-th cluster
: a representative of the m-th cluster
: i-th data point in the m-th cluster
1 K-Means, PAM(K-Medoids), K-modes, CLARA
| K-Menas | PAM (Partitioning Around Medoid) ; K-Medoids | |
|---|---|---|
| ☑️ what) | Centroid를 클러스터의 기준점으로 하는 Pratitioning clustering method | Medoid를 클러스터의 기준점으로 하는 Pratitioning clustering method |
| cf) | centroid는 real data point가 아닌 logical center이다. | medois는 real data point이다. |
| Time Complexity | where t is a # of iteration. | PAM: CLARA: |
| 👍🏻 gd) | k, t << n 이므로 시간복잡도를 으로 상정할 수 있다. | more robust than k-means; outlier의 significant한 효과를 없앨 수 있다. |
| 🥲 pb) | local optimum에 수렴할 수도 있다. Noise, outlier를 다룰 수 없다. | 의 시간복잡도로, 스케일이 어렵다. -> sol) CLARA |
| Variation | K-modes for categorical-only data - data distance: 미스매치 페어 개수, where is - cluster distance: | CLARA (Clusrterin LARge Applications) i) 데이터셋을 샘플링한다. ii) PAM을 적용한다. iii) 전체 데이터를 샘플링 데이터셋의 medoid에 따라 클러스터링한다. - sample size 大 → accurary ↑ , time ↑ - sample size 小 → accuracy ↓ , time ↓ |
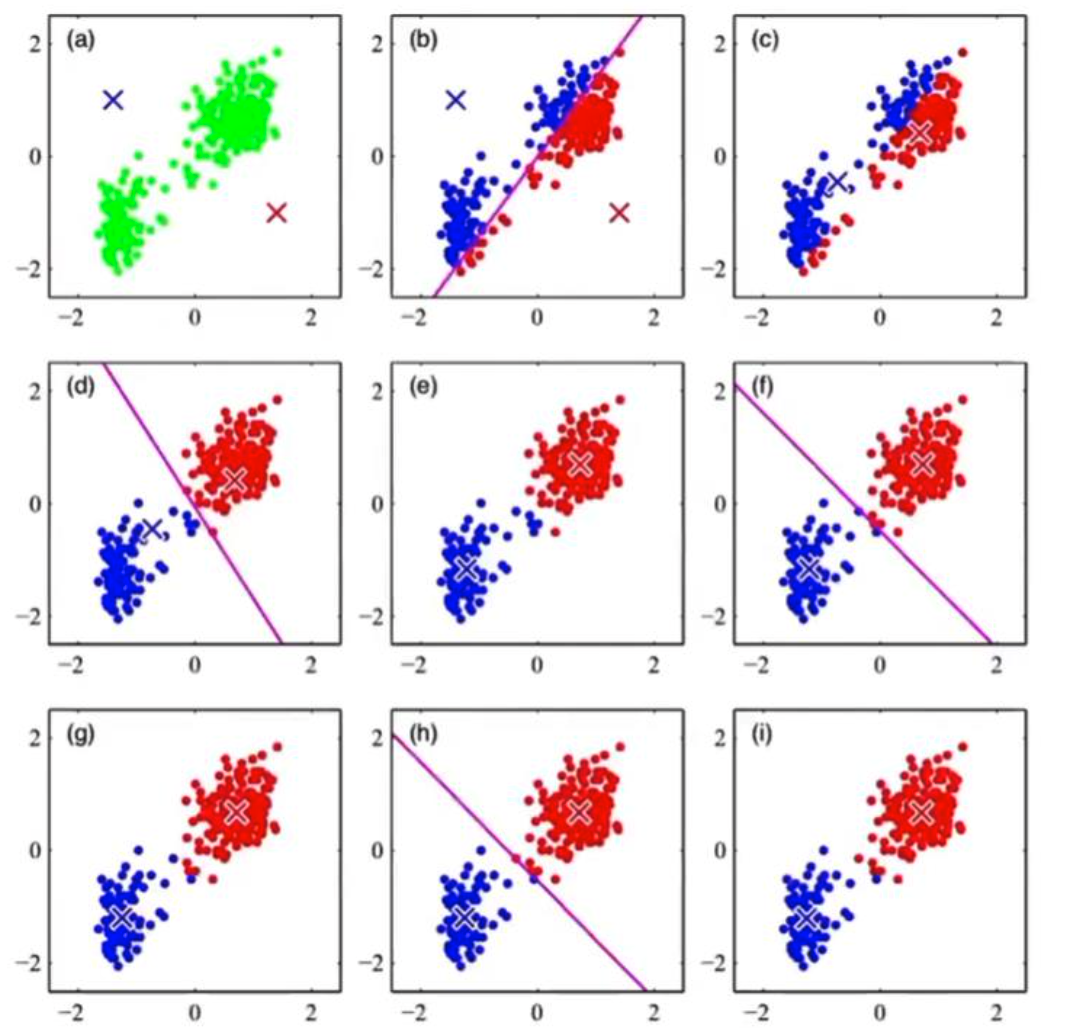
1. K-Means Algorithm
i) 개의 seed point를 무작위로 선택하고, 데이터를 클러스터링한다.
ii) 클러스터의 centroid를 계산하여, 새롭게 데이터를 클러스터링한다.
iii) 클러스터링의 변동이 없을 때까지 반복
2. PAM Algorithm
i) 개의 seed point를 무작위로 선택하고, 데이터를 클러스터링한다.
ii) Total Swapping cost 를 계산한다.
(작성 중)
