1 Data Objects

---

1. Data Set Type

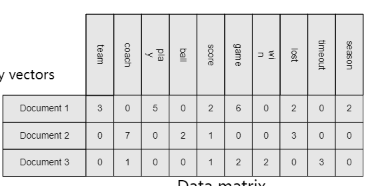
• Tabular $\ni$ Data Matrix, Table
  ex) a set of termm-frequence vectors, trx. data
  
• Graph and Network
  ex) Social Network, World Wide Web, Molecular Structure
• Time Series (ordered)
  ex) video data, temporal data, sequential data
• Etc
  ex) spatial data, image data, multimodal data (video + image)

2. Data Objects

• data set은 data object로 이루어진다.
• data는 특성을 가진다.
• data는 feature에 의해 표현된다.

1) Have Characteristics

• Dimensionality: # of features
  😢 pb) Curse of Dimensionality: 大 dim. -> data obj. 간의 meaninful distance 측정이 어렵다.
• Sparsity: # of vaule of features (희소성)
  😢 pb) Data Spasity Problem: 실세계에서 missing value가 많아서 분석이 어렵다.
• Resolution : 정보의 양, 정확도 (해상도)
• Distribution: Centrality and Dispersion

2) Described by Feature

== dimension, attribute, variable, etc

☑️ measurable property
➰ ex) customer id, name, address, etc

Types

• Nominal : 카테고리, 상태 등 ➰ ex) hair_color = {black, blond, brown, ...}
• Bianry : 2가지 상태
• Ordinal : 순서 O, magnitude not known ➰ ex) size = {xs, s, m, l, xl}
• Numeric: quantitive
  • Ratio-scaled : ratio가 의미 있는 경우 ➰ ex) weight -> 6kg = 2*(3kg)
  • Interval-scaled : diffrence가 의미 있는 경우 ➰ ex) temperature -> 2도, 4도는 2도 차이이다. (2배 차이 X, 2도 -> 4도의 순서 X)

2 Basic Statistics

---

☑️ Central Tendency, Variantion 을 알아본다.
❓ why) data의 더 나은 이해를 위해

1. Central Tendency: Mean, Median, Mode

Mean

• arithmetic mean
• Weighted arithmetic mean
• Trimmed mean
  😢 pb) Mean, outlier에 큰 영향을 받음
  -> sol) Trimmed Mean, Mean 대신에 Median사용

Median

👍🏻 gd) Extreme value (e.g. anomaly, outlier)의 영향 ↓
😢 pb) sortting하여 중앙값을 찾아야하므로 data가 동적인 상황에서는 적용이 어렵다
-> sol) Estimation via interpolation

Mode (최빈값)

👍🏻 gd) Extreme value effect ↓
▶️ use) discrete value에서 많이 사용된다.

Mean, Median, Mode 비교

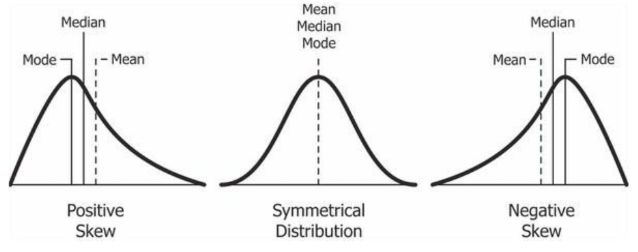
2. Dispersion of Data

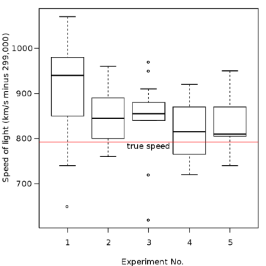
1) Boxplot: 5-number

• 5-number: min, $Q_1$, median, $Q_3$, max
  • Quartile: $Q_1$(25th percentile), $Q_3$ (75th percentile)
    $IQR = Q_3-Q_1$
• Boxplot: 5가지 숫자의 시각화
• Outlier: 주로, 1.5*IQR의 밖에 있는 value
  

2) 분산, 표준편차

Variance and Standard Deviation

• $\sigma^2 = \frac{1}{n} \sum_i (x_i-\mu)^2$
• $S^2 = \frac {1}{n-1} \sum_i (x_i - \tilde x)^2$

• 표본 표준편차에 (n-1)이 나눠지는 이유 -> degree of freedom: sample 표준편차가 모표준편차보다 작은 경향이 있다.

3) 정규 분포

Normal Distribution
rough 하게 data의 분포를 알 수 있다.

3 Visualization

---

1. Boxplot

	2. Histgram	3. quantile plot	4. q-q plot	5. Scatter plot
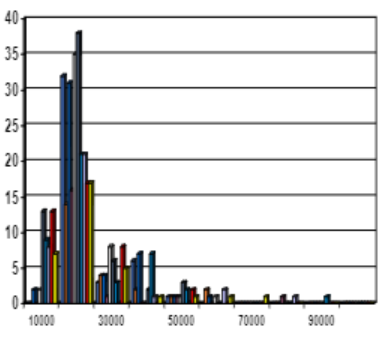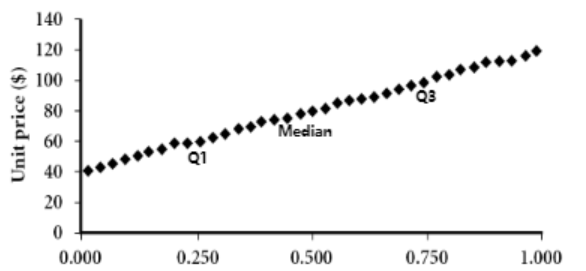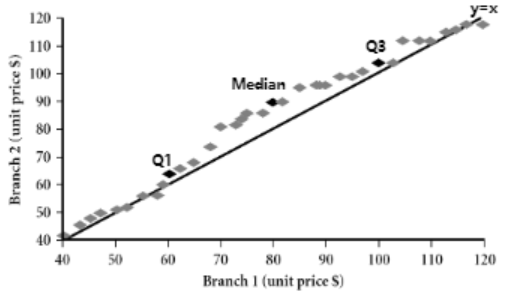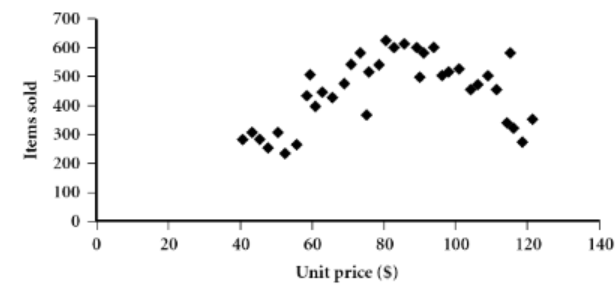☑️ what	데이터를 일정 간격으로 나누어 개수를 나타낸 그래프	오름차순 정렬된 데이터	2 dataset에 대해서, 1 common(shared, same) feature에 대해 비교	1 dataset에서, 2 feature에 대해서 비교
👍🏻 gd)	no overlap, no empty	overall behavior, unusual occurrence (rapid change, seperation)를 파악		cluster, outlier의 overview를 제공, 상관관계 (비례, 반비례)의 유무 파악
➰ ex)			테크노마트와 이마트의 smartphone price 비교	테크노마트에서의 smartphone price와 판매량의 상관관계

4 Similarity & Dissimiliarity

---

1. What is Similarity and Dissimilarity

• similarity: [0, 1], 얼마나 비슷한지
• dissimilarity : [0, $\infty$), 얼마나 다른지
  -Proximity

2. Proximity Measure

Nominal Features

• Simple matching

• Binary Feature로 변환하여 계산하기

bianry Features

• symmetric
• asymmetric

Numeric Features

1. 먼저 standardize/normalize를 수행해야 한다.
   why) 각 feature에 따라 scale이 다르기 때문이다.
2. distance 계산

• Minkowski Distance
  dissym.에 집중
• Cosine Similarity
  sym.에 집중

Ordinal Features

1. Normalize하여 numeric feature처럼 만든다.
2. distance를 계산 한다.

Mixed Type Features

weighted average