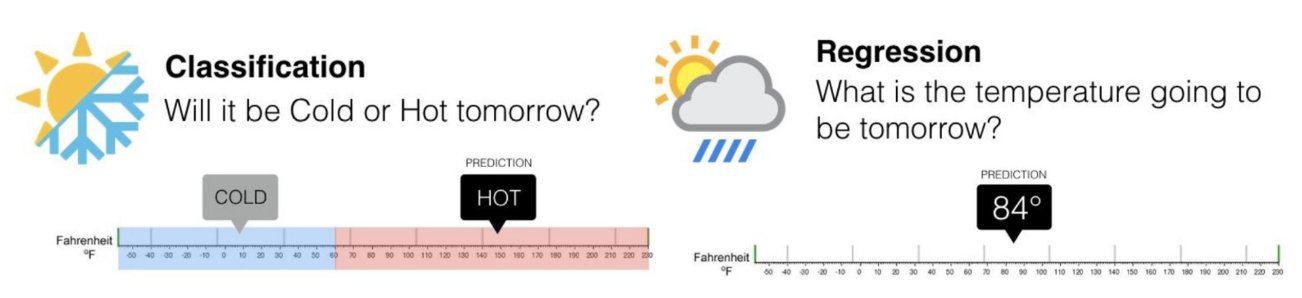
0 What is Classification

---

☑️ categorical class label을 예측하는 일 (Discrete value)
➰ ex) spam mail detection
cf) Regression -> continuous-value 예측

how) to do

1. Model Construction
   $<feat_1, feat_2, ..., feat_n, label>$
   labeled data로 학습한다.
2. Model Usage (Classification)
   $<feat_1, feat_2, ..., feat_n>$ -> $label$
   future, unknown sample을 분류한다.

cf) supervised vs. unsupervised

	Supervised Learning	Unsupervised Learning
data	labeled $<f_1,...,f_n,label>$	unlabeled $<f_1,...,f_n>$
		interested in how does data look like
ex)	classfication	clustering

Issues in Classification

1) Data Preparation

• Data Cleaning
  • noise, missing value, outlier, error, etc
• Relevance Analsys
  • useful feature 만을 추출하여야 한다.
  • correlation analysis 등을 활용할 수 있다.
• Data Transformation
  • Generalize
  • Normalize

2) Evaluation

• Accuracy
• Speed
  • Training time
  • Test time
• Robustness
• Scalability
• Interpretability
  

1 Decision Tree & Random Forest

---

intuitive & important

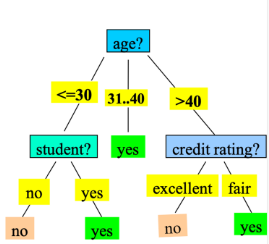
1. Decision Tree

모든 가능한 결정의 Graphical Representation

• Branch node → choice
• Leaf node → decision

1) Decision Tree Induction

☑️ Decision Tree 만드는 법

• recursive, top-down, divide-and-conquer
• greedy

start with empty tree
repeat {
	if no feature or no branch : break;
	else:
		select a feature
		make a tree
}

2) Homogeneous Feature Selection $\ni$ ID3, C4.5, CART

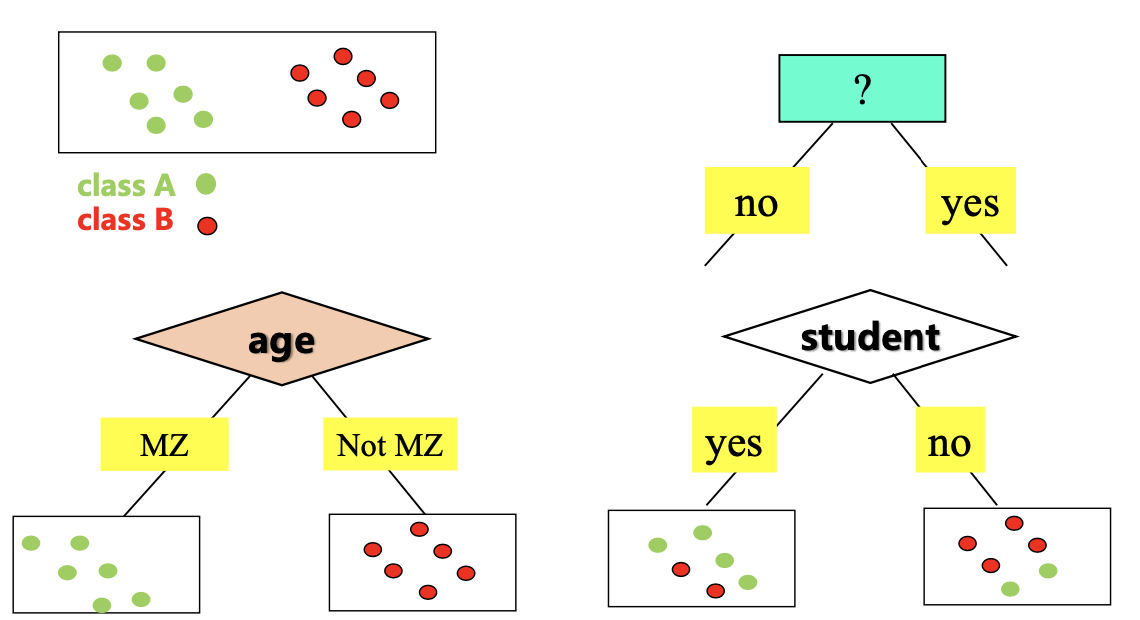
	Homogeneous	Heterogeneous
data	paritioned	mixed
Entropy (== Info(D))	小	大

ID3 : Entropy

(Iterative Dichotomiser 3)

☑️ Information Gain을 최대화하는 feature를 선택하여 분기한다.
$Gain(f) = Info(D) - Info_F(D)$

• where $f$ is a feature
• Before Entropy : whole dataset entropy
  $Info(D) = \sum_i (-p_ilog_2p_i)$
• After Entropy : weighted average of each entropy
  $Info_f(D) = \sum_i \frac{|D_i|}{|D|}Info(D_i)$

😢 pb) Bias problem: 多 value를 가진 feature의 $Gain$이 큰 경향이 있다.
❓ 더 많이 나뉠수록 well partitioned되는 것처럼 보이기 때문이다.
→ sol) C4.5

C4.5 : Gain Ratio

☑️ ID3의 bias problem을 penalty term 보완한 버전
$GainRatio(f) = Gain(f)/SplitInfo_f(D)$

• $SplitInfo_f(D) = \sum_i(-\frac{|D_i|}{|D|} log_2\frac{|D_i|}{|D|})$

CART

(Classification And Regression Trees)

☑️ MSE(Mean Squared Error)를 최소화하는 feature를 선택하여 분기한다.
$\Delta gini(A) = gini(D) - gini_A(D)$

• $gini(D) = 1-\sum p_i^2$
• $gini_A(D)=\frac {|D_1|}{|D|} gini(D_1) + \frac {|D_2|}{|D|} gini(D_2)$

2. pb&sol

pb) Overfitting -> sol) Tree Pruning, Random Forest

1) Tree Pruning

• Pre-prunning : Halt during construction of tree
  • goodness measure를 정의해야 한다.
  • threshold를 정의해야 한다.
• Post-prunning : Remove from a fully grown tree
  • 학습 전에 validation set을 준비한다.
  • node의 pruninng version이 not worse 하다면 그 node를 제거한다.

2) Random Forest

다음에서 설명

3. Random Forest

☑️ Decision Tree Ensemble을 활용하여 classification 하는 방법

how) to make

1. Decisiton Tree 학습
   1) 학습 데이터셋 Bootstrap Sampling: #(Data) 만큼 original dataset에서 random sampling (* data 중복 가능)
   2) Randomly select several features
   3) N번 반복
   
2. Aggregation
   -Majority voting : $\hat y_{Ensemble} = argmax_i(\sum \hat y = i), i\in {0, 1}$
   -Weighted Voting

2 Classification 방법들

---

1) Rule-Based Classification

☑️ IF-THEN rules에 기반하여 분류
▶️ use) domain expert에 의해 rule을 만들 수 있으므로 data가 적거나/없는 경우에 사용
😢 pb) conflict
-> sol) confilct resolution
1. size ordering: tough requirement부터 우선순위 (*tough == specific == 多 values)
2. class-based ordering: class에 순서를 부여
3. rule-based ordering: rule에 순서를 부여

2) Associative Classificaton

☑️ Rule Extraction from Association Rule Mining
min_sup, min_conf를 조절하여 rule들을 추출할 수 있다.
👍🏻 gd) 大 min_conf -> confident association을 추출할 수 있다.
😢 pb) 大 min_conf -> low coverage

😢 pb) rules are not mutually exclusive
-> sol) conflict resolution
cf) Rule Extraction from Decision Tree -> mutually exclusive

Coverage and Accuracy of rule R

$coverage(R) = \frac{\# (covered)}{|D|}$

$accuracy(R) = \frac{\# (correct)}{\#(covered)}$

3) Lazy Learners

Eager Learning vs. Lazy Learning

	Eager Learning	Lazy Learning
Learning	Before 분류	Wait til 분류
👍🏻 gd		much 小 time in training
😢 bd		more 大 time in 분류

ex) KNN (K-Nearest Neighbor)

☑️ 분류 알고리즘
1. 데이터 간의 distance 결정 방법을 정의한다.
2. K개의 distnace가 가까운 데이터 점들을 모은다.
3. K개로 분류를 수행한다. -> Majority Voting | Weighted Voting

3 Accuracy and Error Measures

---

1. 평가 measure

• 정확도 $Accuracy = \frac {True}{Total}$
• 민감도
  $Sensitivity(Recall) = \frac {TruePositive}{Positive}$
• 정확도
  $Preicision = \frac {TP}{TrueP+FP}$
• 특이도
  $Specificity = \frac {TN}{Negative}$
• F1-score $2*\frac {recall*precision}{recall+precision}$

2. 평가 방법

• Holdout method
  training/test partition을 random하게 k번 반복하여 average of accuracy를 측정
• Cross-Validation (k-fold cross validation)
  k개의 disjoint subset (D1, D2, ...., Dk) 으로 나누어서 각 subset을 test et, 나머지를 training set으로 사용한 모델의 accuracy 평균 측정
  k = 5, 10
  • Leave-one-out
    k = 1
  • Stratified cross-validation
    each fold distribution: same as original data dist.

4 Ensemble

---

k개 model의 결합 for aggregation of 多 opinions
1. Bagging
2. Boosting
3. Model Ensemble

1. Bagging

(Bootstrap AGgregation)

Bootstrap을 여러 개 smapling 하여 모델을 만들고 majority voting으로 classification을 수행한다.
ex) Random Forest, NN ensemble, ...\

2. Boosting: Bagging + Weight

1. Initial weights to 1/d (where d is $\#(data)$, $sum(weight)=1$)
2. Iteration
   1) Train $M_i$ with $B_i$
   2) Test $M_i$ with $T_i$
   3) Update Weight (misclassified는 높이고, 나머지는 줄인다.
3. 의사 결정 시에, 각 모델의 accuracy가 weight가 된다.