0 Basic Concepts and a Road Map

---

1. Frequent Pattern Mining

☑️ FP: dataset에서 자주 나타나는 패턴.
❓ why) Finding inherent patterns in huge data
➰ ex) subsequences in DNA, substructures in GULF, co-purchased items in ITEM

2. Basic Concepts

• $Support: P(X)$ (just frequency)
  • Probability that a trx contains $X$.
  • Minimum support: a threshold
• $Confidence: P(\frac {X \cup Y}{X})$
  • Conditional probability that a trx containing $X$ also contains $Y$.
  • Minimum confidence: a threshold

Frequent Pattern

$X \quad where \ \ sup_X > sup_{min}$

Association Rules

$X→Y \quad where \ \ sup_{XY} > sup_{min}\ ,\ conf_{X->Y} > conf_{min}$

Closed & Max

▶️ use) FP가 너무 많은 경우 == useless patterns가 많은 경우

• Closed Pattern

  • same support인 FP들 중
  • super pattern 無 인 FP

• Max Pattern

  • FP들 중
  • super pattern 無인 FP

1 FP mining Method

---

❓ data가 매우 많으므로 reasonable time에 결과를 내기 위해서는 Scalable(==efficient == speed-up) 한 알고리즘이 필요하다.

0. Downward Closure Property of FP

FP의 특성으로, FP mining은 이 특성에 기반한다.

• FP이면, 그 subset도 FP이다.
• FP가 아니면, 그 superset도 FP가 아니다. (contraposition)

• ${a, b, c}: FP → {a, b}: FP$
• ${a, b} : \neg FP → {a, b, c} : \neg FP$ (→ This can be used for pruning)

1. Apriori : Candidate Generation-and-Test Approach

☑️ Candidate Generation-and-Test Approach를 사용하는 FP mining Algorithm

❕ How

1. 1st scan DB: get 1-itemset FP
2. Repeat [k] (where k is length of itemset)
   1) [k + 1]-Candidate를 생성한다. (self-joining [k]-FP -> pruning1)
   2) 각 candidate가 FP인지 확인. (scan DB) (pruning2)
   3) no FP || no Candidate 면 종료

Pseudo-code

C_k = candidate set of size k
L_k = frequent set of size k
L_1 = {freqiemt items};
for k = 1; L_k != {}; k++ {
	generate C_k+1
    for trx in database:
    	count C_k+1
	L_k+1 = elements over min_sup in C_k+1
}
return union of L_k	

🥲 Pb)

1. 多 DB scan (disk IO 에바징,,)
2. 多 candidate, pruning에도 불구하고 (특히 k=1에서 많으면 k=2에서 반드시 많게 됨)
3. 多 workload (특히 candidate의 support counting)
   ex) 100개 item -> 100 scans, $2^{100}-1$ candidates

sol) general ideas

1. DB scan ↓
2. candidate 수 ↓
3. candidate support counting을 고도화

Sol) DIC, Partition, Sampling, DHP

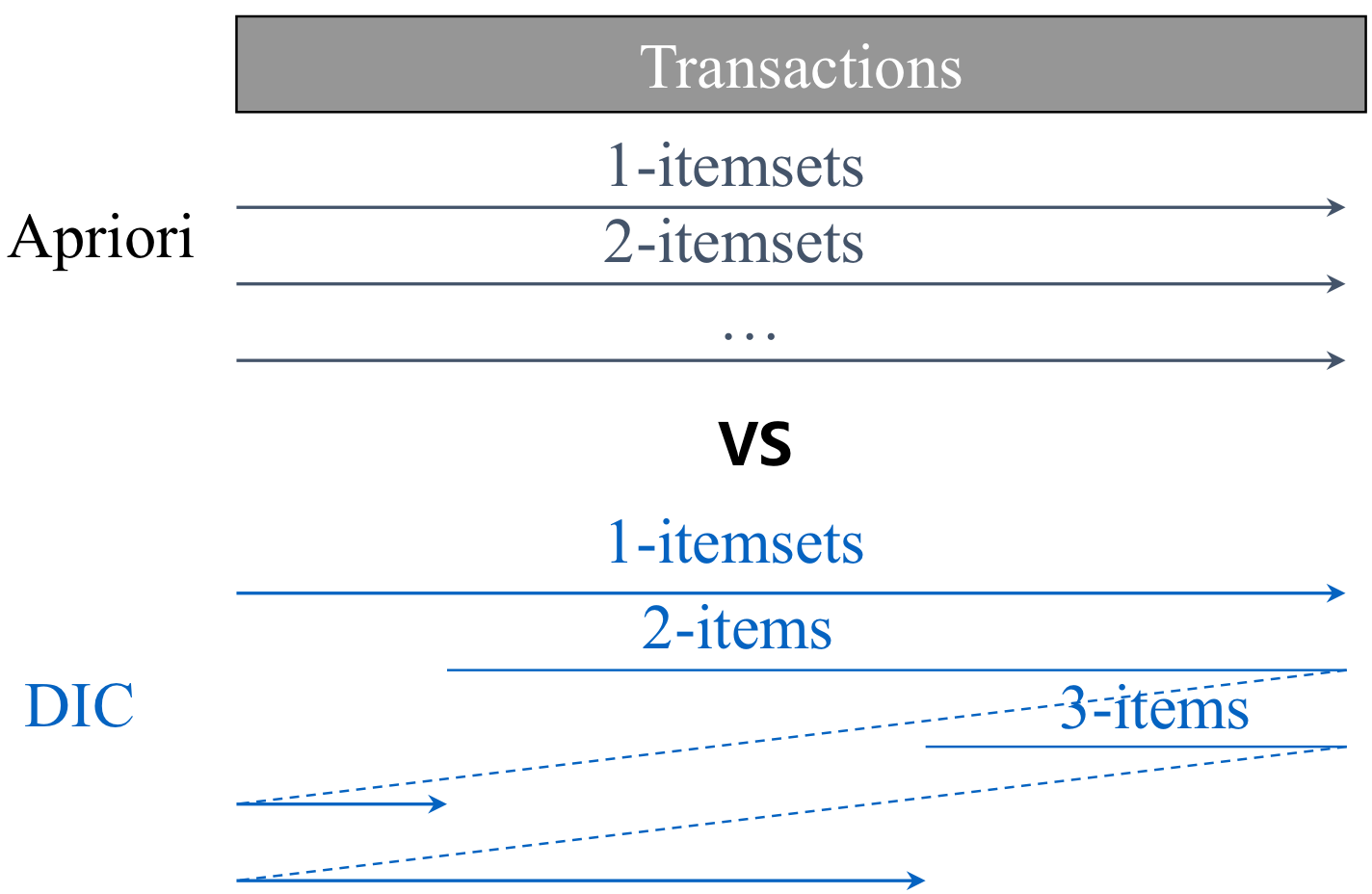
1. DIC (Dynamic)

(Dynamic Itemset Counting)

☑️ candidate-generation-and-test를 동적으로 수행하는 알고리즘
-> [k]에서 k-candidate만을 counting하지 않고, k+1-candidate도 생성하여, 생선한 즉시 support counting을 시작한다.
👍🏻 gd) DB scan ↓

2. Partition (2 scan)

☑️ DB을 분할하여 각 partition에서 apriori를 수행하는 알고리즘
👍🏻 gd) 2 DB scan
👍🏻 gd) guarantee ALL FP (❓global FP는 at least one partition에서 local FP가 된다.)

❕ how) algorithm
1) DB를 main memory에 fit하게 k개로 나눈다.
2) local FP를 구한다. → local_min_sup = min_sup/k
3) global FP인지 테스트한다.

3. Sampling

☑️ DB에서 random smapling으로 SDB(Sample DB)를 만들어 Apriori를 수행하는 알고리즘
👍🏻 gd) DB scan ↓, candidate 수 ↓

🥲 pb) not global FP 可, FP missed 可
-> sol) 2 more scan
1. Verify FP and its negative borders (NB: S에는 없으나, S에 모든 subset들이 있는 경우 + single items)
2. NB

4. DHP (Hashing)

(Direct Hashing and Pruning)

candidate를 해싱을 이용하여 pruning하며 Apriori를 수행하는 알고리즘
👍🏻 gd) candidate 수 ↓

how)
1. Hashing: [k] 각 trx에서 k+1-candidate를 만들고 해싱한다.
2. Pruning: 해싱 테이블에 기반하여 candidate를 pruning하고 test

2. FP-growth

☑️ Apriori의 main bottleneck인 candidate-genration-and-test 과정 없이 FP를 찾기 위해 고안된 FP mining 기법
👍🏻 gd) candidate generation & test 가 없다
👍🏻 gd) FP-tree가 compressed DB의 역할을 하여 데이터를 메모리 내에서 다룰 수 있다. -> 2 scan of DB (FP-tree 만드는 과정에서 2번)

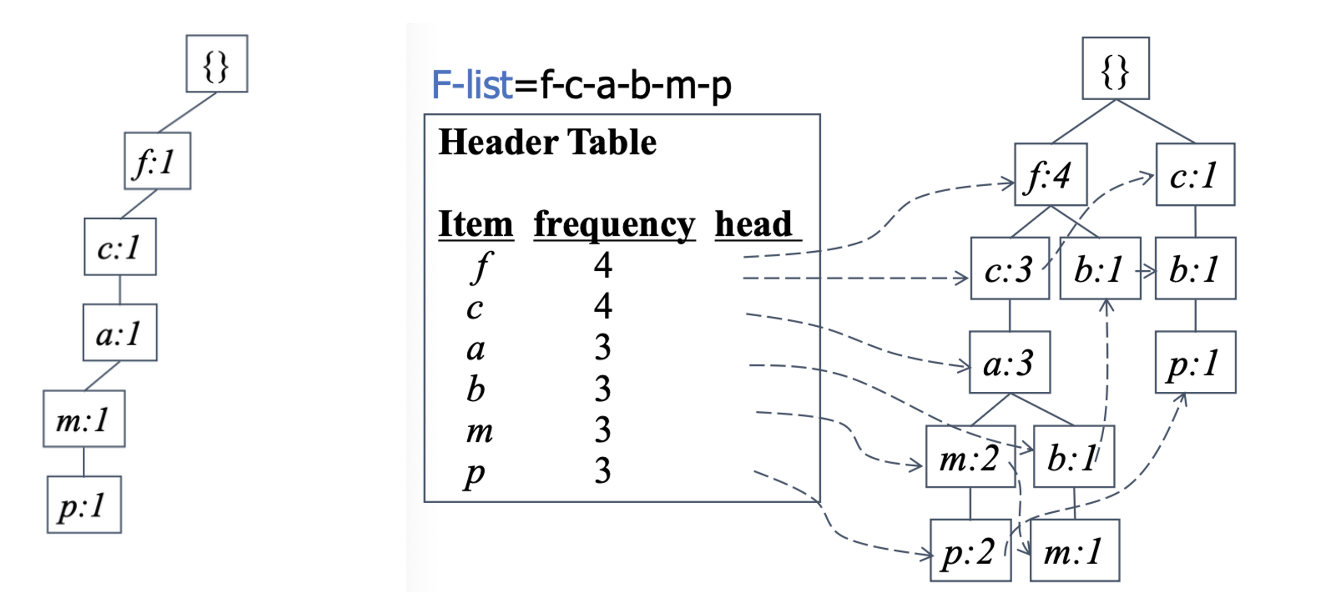
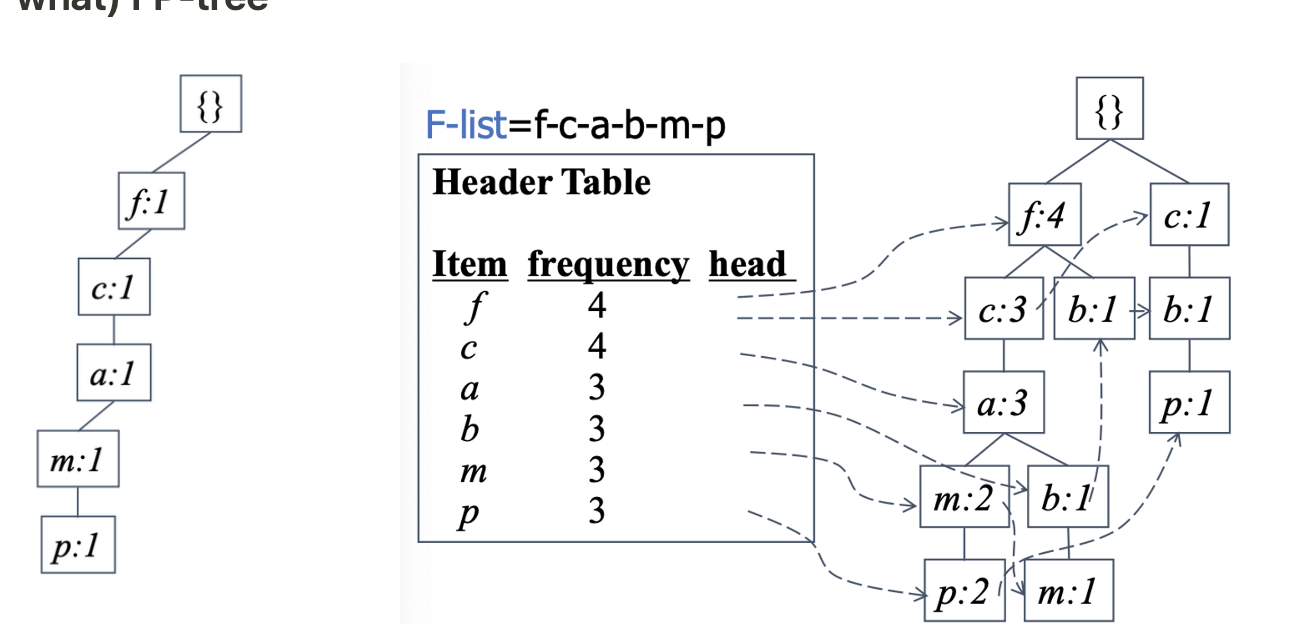
1) FP-tree

☑️ FP-Growth에서 사용되는 자료구조이다.

• 3 자료구조 : F-list, Header Table, FP-tree
  
  👍🏻 gd) Completeness : lossless info.를 가진다.
  👍🏻 gd) Compactness : infrequent item이 없어서 compact하므로 매모리에 올라올 수 있다, freq 할수록 더 위에 있으므로 공유될 가능성 ↑

how) to make

1. Scan DB, find frequent 1-itemsets
2. Make F-list: Sort 1-FP in frequencey descending order(strict order가 있어야 함)
3. Scan DB,
   1) F-list를 사용하여 각 trx를 배열한다.
   2) Construct FP-tree

2) How to find FP: divide-and-conquer

1. Divide → Target FP를 disjoint subset으로 partitioning
2. Conquer → each parition에서 F-list를 사용하여 conditional patt-base와 conditional FP-tree를 생성한다.
   1. conditional FP-tree가 single path, empty 멈춘다.
   2. branch가 있다면 recursion

3) cf) FP-Growth vs. Apriori

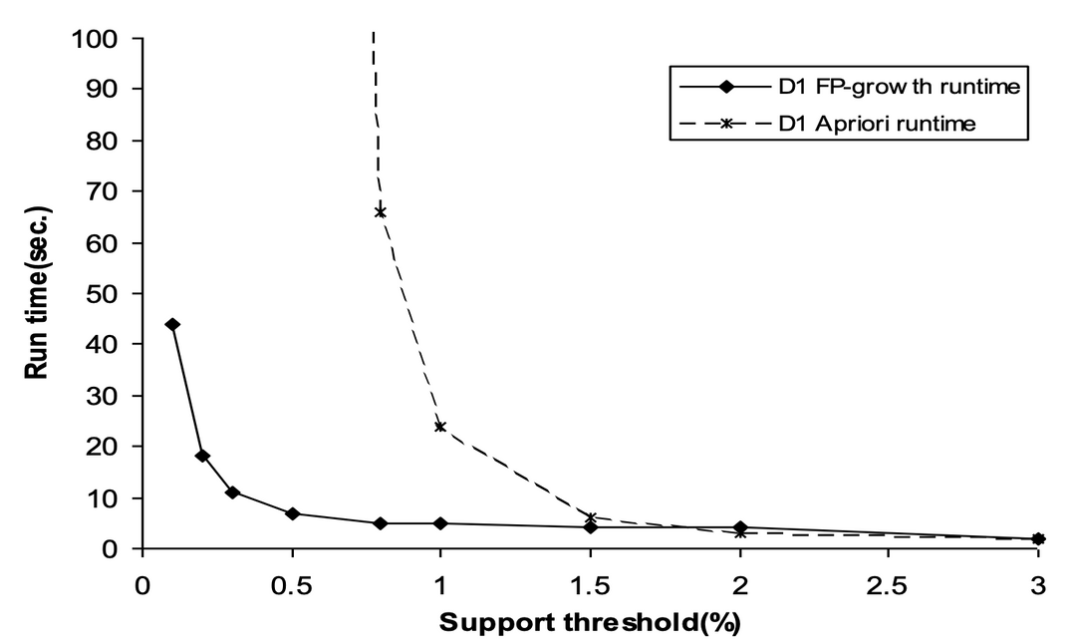
• 大 min_sup → Apriori에서 생성&테스트 candidate의 수가 절대적으로 적어지므로 두 알고리즘의 차이가 거의 없다.
• 小 min_sup → FP-Growth에서는 candidate generation and test가 없으므로 압도적으로 성능이 좋다.

3. Max Miner

Mining Max Patterns
$\forall$ FP X
only max-pattern O

1. 1-FP를 찾고 ascending order로 정렬한다.
2. 2-FP부터 potential max-pattern을 찾는다. by set-enumeration tree

👍🏻 gd) 2-FP부터 potential max-patt.을 검사하면 이후 단계에서 candidate의 수가 줄어든다. (BCDE O → BCD, BDE, CDE 체크할 필요 X)

4. CLOSET

Mining Closed Patterns
FP-growth 중에 closed pattern을 찾을 수 있다.

m-conditional base에서 closed patt. 찾기

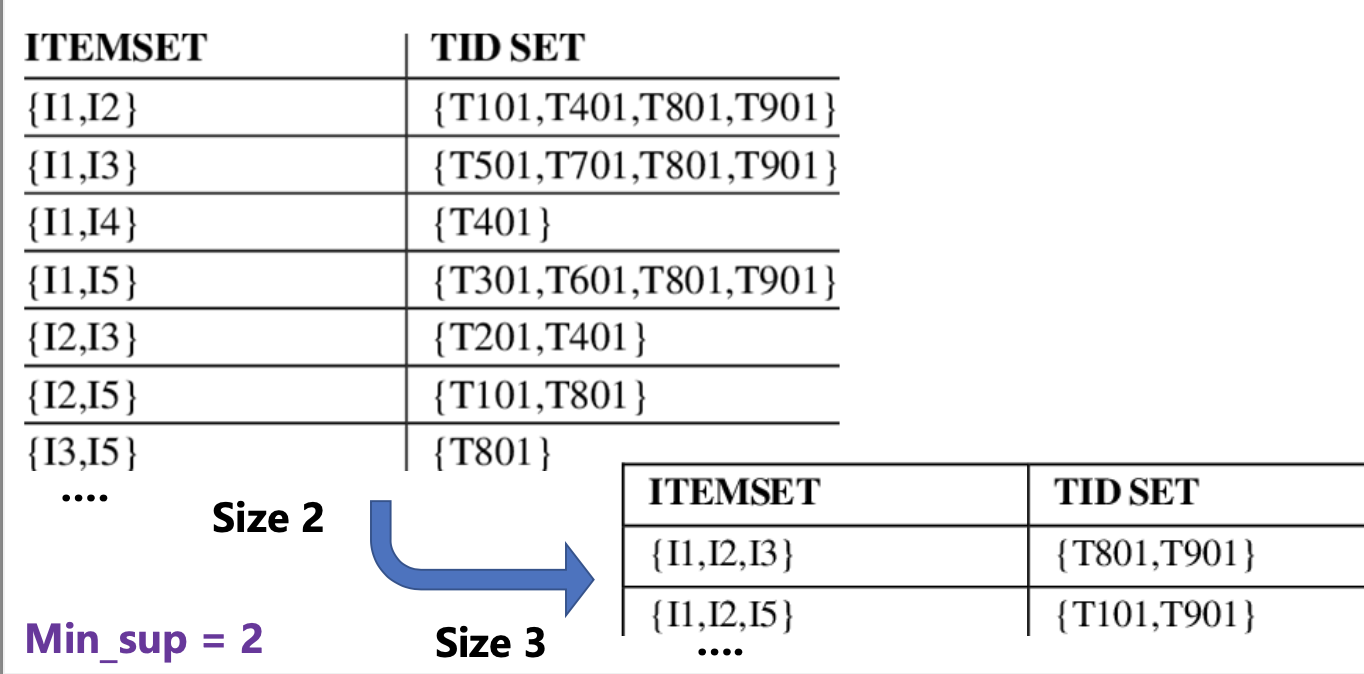
5. CHARM

(Closed itemset based High Utility Rare Itemset Mining)

Vertical format 을 활용하여 FP를 찾는다.
👍🏻 gd) 교집합 operation으로 candidate를 얻을 수 있다.
👍🏻 gd) length가 frequency이다

1. 1 FP itemset들을 vertical format으로 바꾼다.
2. k + 1 size의 FP itemset을 찾는다. (교집합 + APriori property)
   

2 Association Rules

---

1. Multi-Level Association Rules

Item은 hierarchies를 가지므로 flexible min_sup을 설정한다.
ex) milk (10%) $\ni$ 매일우유(6%), 서울우유(4%)
❓ 다른 계층에 같은 minimum support를 적용하는 것은 unfair
goal) 다른 계층의 같은 아이템들이 최대한 같게 FP에 포함되도록 (milk가 FP면 매일우유&서울우유도 FP가 되도록)

Redundancy Filtering

ancestor rule
descendant rule

descendant support가 ancester support에 의해 expected value이면 redundant

2. Multi-Dimensional Association

• single-dim. -> buy(milk) -> buy(bread)
• multi-dim.
  • inter-dim. -> age(19-25) ^ occupation(student) -> buy(coke)
  • hybrid-dim. -> age(19-25) ^ buy(popcorn) -> buy(coke)

3. Quantitative Association

Attribute(Feature) 유형

• Categorical -> finte, order X
• Quantitative -> numeric, order O

  numeric feature로부터 연관 규칙 찾기

1. Design the format of association rule.
2. Discretize the features
3. Make a grid
4. Calculate each cell

*adjacent cell이면 합칠 (cluster) 수 있다.

3 From Association Mining to Correlation Analysis

---

ex) play basketball -> eat cereal (0.4, 0.67)
🥲 pb) meaningful해 보이지만 사실 eat cereal은 75%이다.
-> sol) interstingness measure : lift
$lift = \frac {P(A \cap B)}{P(A)P(B)}$

• $lift > 1$ -> positive correlation
• $lift = 1$ -> independent
• $lift < 1$ -> negative correlation