Confusion_Matrics, precision, recall, precision_recall_curve

분류분석의 평가지표로 실제값과 예측값을 통하여 얼마나 잘 예측했는가를 평가할 수 있는 지표이다.

실습을 통하여 확인해 보겠습니다.

from sklearn.metrics import confusion_matrix, precision_score,recall_score ,accuracy_score
import numpy as np

y_test = list(np.zeros(405))+list(np.ones(45))
fakepred = list(np.zeros(420))+list(np.ones(30))

print(confusion_matrix(y_test,fakepred))
print(f'정확도: {accuracy_score(y_test,fakepred)}')
print(f'정밀도: {precision_score(y_test,fakepred)}')
print(f'재현율: {recall_score(y_test,fakepred)}'

[[405 0][ 15 30]]
정확도: 0.9666666666666667
정밀도: 1.0
재현율: 0.6666666666666666

precision_recall_curve

분류알고리즘은 바로 label값을 예측하는 것이아닌 그확률을 통하여 임계값 0.5를 기준으로 큰 레이블을 출력해준다

그러나 그 임계값을 변화함에 따라 precision값과 recall 값 사이에 trade_off 가 있으므로 적절한 임계값을 찾는것이 중요하다.

이 알고리즘을 사용하기 전에 sklearn안에 있는 Binarizer를 통하여 임계값을 변화함에 따라 결과값이 어떻게 변화는지 확인해 보겠습니다.

from sklearn.preprocessing import Binarizer
from sklearn.metrics import accuracy_score, precision_score, recall_score,confusion_matrix, f1_score

# Binarizer 의 threshold 설정값, 분류 결정 임계값임
# threshold 기준값보다 같거나 작으면 0을 크면 1을 반환
custom_threshold = 0.5

# predict_proba() 반환값의 두번째 컬럼 , 즉 positive클래스 컬럼 하나만 추출하여 Binarizer를 적용
pred_proba_1 = pred_proba[:,1].reshape(-1,1)

binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)


def get_clf_eval(y_test,pred):
    confusion = confusion_matrix(y_test,pred)
    accuracy = accuracy_score(y_test,pred)
    precision = precision_score(y_test,pred)
    recall = recall_score(y_test,pred)
    f1 = f1_score(y_test,pred)
    print('confusion matrix')
    print(confusion)
    print(f'정확도: {np.round(accuracy,4)},정밀도{np.round(precision,4)}, 재현율{np.round(recall,4)}, f1_Score{np.round(f1,4)}')
    
get_clf_eval(y_test,custom_predict)

confusion matrix
[[245 21][ 2 150]]
정확도: 0.945,정밀도0.8772, 재현율0.9868, f1_Score0.9288

적절한 임계값을 찾기 위한 for 구문

import numpy as np
from sklearn.preprocessing import Binarizer
from sklearn.metrics import accuracy_score, precision_score, recall_score,confusion_matrix

def get_clf_eval(y_test,pred):
    precision = precision_score(y_test,pred)
    recall = recall_score(y_test,pred)
    return (precision,recall)

threshold_arr = np.linspace(0,1,num=20,endpoint=False)
precision_list = []
recall_list = []

for i in threshold_arr:
    # threshold 객체내의 값을 차례로 iteration하면서 evaluation 실행
    binarizer = Binarizer(threshold=i).fit(pred_proba[:,1].reshape(-1,1))
    custom_predict = binarizer.transform(pred_proba[:,1].reshape(-1,1))
    precision,recall =  get_clf_eval(y_test,custom_predict)
    precision_list.append(precision)
    recall_list.append(recall)
print(precision_list)
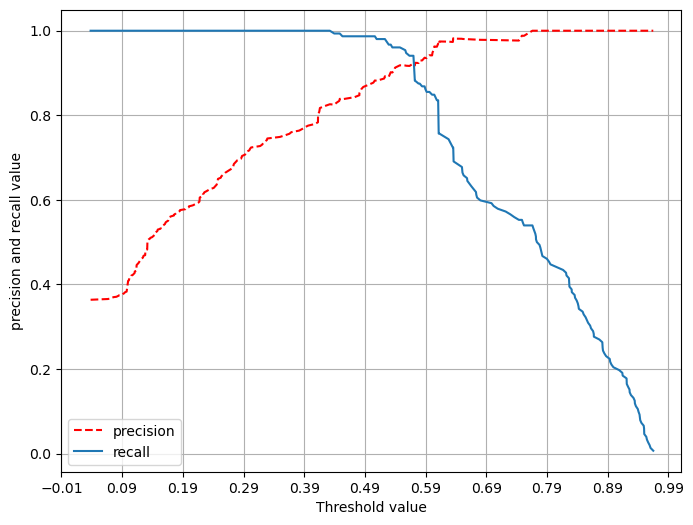
print(recall_list)

[0.36, 0.36, 0.40, 0.53, 0.58, 0.65, 0.72, 0.75, 0.77, 0.83, 0.87, 0.91, 0.94, 0.98, 0.97, 0.98, 1.0, 1.0, 1.0, 1.0][1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.98, 0.98, 0.95, 0.84, 0.66, 0.58, 0.54, 0.44, 0.32, 0.19, 0.05]

위의 결과를 통하여 절충관계를 확인 할 수 있다.
좀 더 가시성을 높이기 위하여 그래프를 통하여 확인 할 수 있다. sklearn에 있는 precision_recall_curve라이브러리는 precision,recall,thresholds를 출력물로 준다 이 출력값을 통하여 plot을 그려보겠습니다.

from sklearn.metrics import precision_recall_curve
from sklearn.linear_model import LogisticRegression

lr_clf = LogisticRegression()
lr_clf.fit(x_train,y_train)

# label이 1인 값의 두번째 열만 사용
pred_proba = lr_clf.predict_proba(x_test)[:,1]

precisions, recalls,thresholds = precision_recall_curve(y_test,pred_proba)
print('threshold 5 sample',thresholds[:5])
print('precision 5 sample',precisions[:5])
print('recall 5 sample',recalls[:5])

threshold 5 sample [0.03812389 0.05315255 0.06611711 0.07033047 0.07142196]
precision 5 sample [0.36363636 0.36450839 0.36538462 0.36626506 0.36714976]
recall 5 sample [1. 1. 1. 1. 1.]

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

def precision_recall_curve_plot(y_test,pred_proba):
    precisions, recalls,thresholds = precision_recall_curve(y_test,pred_proba)
    
    plt.figure(figsize=(8,6))
    threshold_index = thresholds.shape[0]
    plt.plot(thresholds,precisions[0:threshold_index],'r--',label='precision')
    plt.plot(thresholds,recalls[0:threshold_index],label='recall')
    
    start,end = plt.xlim()
    plt.xticks(np.around(np.arange(start,end,0.1),2))
    
    plt.xlabel('Threshold value')
    plt.ylabel('precision and recall value')
    plt.legend()
    plt.grid()
    plt.show()
    
precision_recall_curve_plot(y_test,pred_proba)