단순 선형 회귀
- 입력 특성에 대한 선형 함수를 만들어 예측을 하는 알고리즘
- 독립변수가 하나인 경우 특정 직선을 학습하는 것
- 선형 회귀 모델을 잘 한습시키려면 MSE(평균 제곱 오차)값을 최소화 하는 파라미터 선택
- 통계적 방식의 회귀 분석은 정규방정식을 사용하여 문제를 해결
- 머신러닝 모델에서는 경사하강법을 사용하여 위의 문제를 해결
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
data = pd.read_csv('./data/insurance.csv')
data
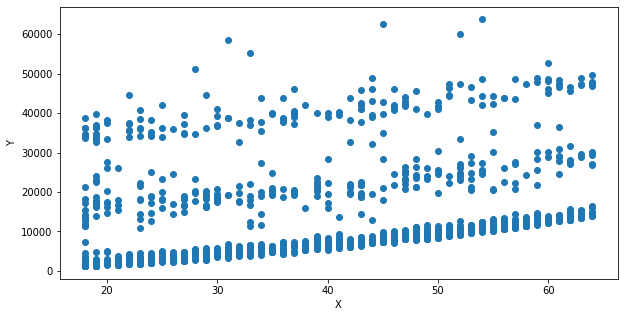
## 나이와 의료비용 사이의 선형임을 확인
x=data['age']
y=data['charges']
plt.figure(figsize=(10,5))
plt.scatter(x,y)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
LinearRegression()
- 매개변수
- fit_intercept
- 데이터의 타입은 bool 기본값은 True
- 선형 회귀 모델에 대한 절편을 계산할지 여부 결정
- normalize
- 데이터의 타입은 bool 기본값은 False
- True인 경우 X는 평균을 빼고 L2-norm으로 나누어 회귀 전에 정규화
- False인 경우 해당 정규화 X
- copy_x
- 데이터의 타입은 bool 기본값은 True
- True이면 X가 복사
- False이면 덮어씌운다
- n_jobs
- 데이터의 타입은 int 기본값은 None
- 계산 작업 횟수
- postive
- 데이터의 타입은 bool 기본값은 False
- True로 하면 계수가 양수
- 속성
- coef_
- 데이터의 타입은 array
- 선형 회귀 문제에 대한 추정된 계수
- rank_
- singular_
- intercept_
- 메서드 ( [] 안의 인자 값은 생략 가능 )
- fit(x, y, [smaple_weight])
- 모델 학습 메서드
- x : 학습 데이터, 2차원 array형태로 입력
- y : 타깃데이터
- sample_weight : 개별 데이터에 대한 가중치
- 선형 회귀 모델의 추정기를 오브젝트로 반환
- get_params([deep])
- 선형 회귀 모델의 매개변수를 출력
- deep : bool의 형태로 입력, 기본값은 True
- 값에 매칭되는 파라미터의 이름을 딕셔너리 형태로 반환
- pridict(x)
- 선형 모델을 사용해 예측
- x : 데이터 샘플
- 예측값을 array로 반환
- score(x, y, [sample_weight])
- 예측의 결정 계수를 반환
- x : 테스트 샘플 array로 입력
- y : x의 실제 값
- sample_weight : 개별 데이터에 대한 가중치
x=np.array(data['age'])
y=np.array(data['charges'])
x=x.reshape(1338 ,1)
# .reshape()으로 차원 맞추기
y=y.reshape(1338 ,1)
lr = LinearRegression()
## fit을 이용해 모델 학습
lr.fit(x,y)
print('선형 회귀 모델 결과')
print('절편', lr.intercept_, '계수', lr.coef_)
## 결정 계수가 8% 낮게 나온다
print(lr.score(x,y))
## 의료비용 예측
## 19세와 64세의 의료비용 예측 값
x_new=[[19],[64]]
y_hat=lr.predict(x_new)
print(y_hat)
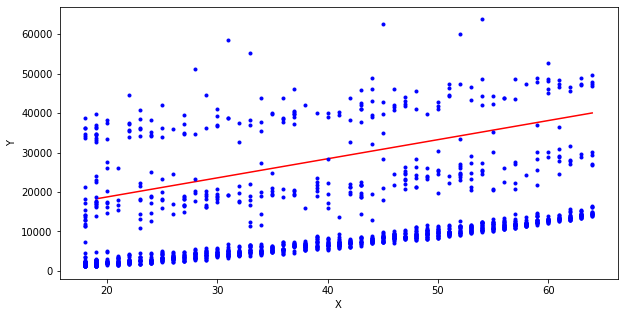
## 산점도 위에 회귀선을 그어 시각화
plt.figure(figsize=(10,5))
plt.plot(x_new, y_hat, '-r')
plt.plot(x, y, 'b.')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
경사 하강법
- 함수의 값이 낮아지는 방향으로 독립 변수의 값을 바꿔가면서 최종적으로 최소 함수값을 갖도록 하는 독립 변수값을 찾는 방식
import pandas as pd
import numpy as np
from sklearn.linear_model import SGDRegressor
data= pd.read_csv('./data/insurance.csv')
x=np.array(data['age'])
y=np.array(data['charges'])
x=x.reshape(1338 ,1)
# .reshape()으로 차원 맞추기
y=y.reshape(1338 ,1)
### max_iter : 훈련 데이터에 대한 최대 패스 수
sgd_reg =SGDRegressor(max_iter=1000, random_state=34)
sgd_reg.fit(x,y.ravel())
print('SGD 회귀 모델 결과')
print('절편', sgd_reg.intercept_, '계수', sgd_reg.coef_)
x_new=[[19],[64]]
y_hat=sgd_reg.predict(x_new)
print(y_hat)
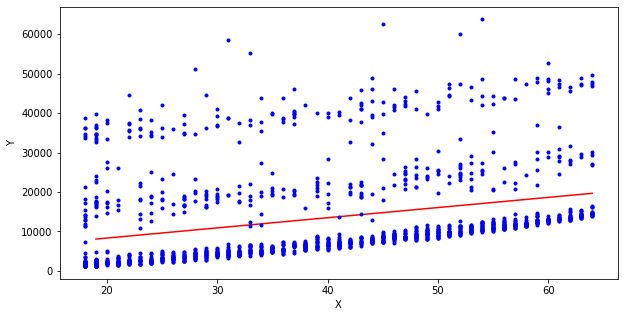
plt.figure(figsize=(10,5))
plt.plot(x_new, y_hat, '-r')
plt.plot(x, y, 'b.')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()