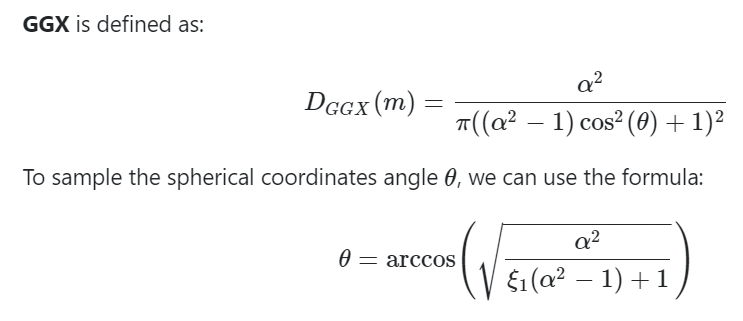Importance Sampling

이전 몬테카를로 적분 포스팅에서 다뤘던 몬테카를로 적분 식이다.
Importance Sampling은 이 식에서 $p(x_i)$를 어떻게 설정하면 더 적분값의 분산이 적어질지에 대한 방법론이다.

개념

일단 확률에 관한 이야기가 많이 나오니 개념부터 정리한다.

• 확률 변수(Random Variable): 랜덤 프로세스에 의해 나올수 있는 결과값(실수)
• 기댓값(Expectation Value): 랜덤 프로세스를 행했을때 마땅히 나오길 기대하는 값(평균)
• PDF(Probability Density Function): 확률변수가 가질수 있는 값을 가로축, 확률값을 세로축으로 가지는 함수, 모든 구간을 적분하면 무조건 1.
• 분산(Variance) : 랜덤 프로세스의 결과로 나오는 값이 기댓값과 벌어진 정도(양의 실수)

Importance Sampling이란?

아주 간단히 한줄 정리도 가능하다.
Importance Sampling은 몬테카를로 추정량

의(몬테카를로 추정량 자체를 확률변수로 봤을때 몬테카를로 추정량의 기댓값은 실제적분값임) 분산을 줄이기 위해서 $p(x_i)$를 '잘' 선택해보는 방법이다.

원함수$f(x_i)$를 알아도 $p(x_i)$를 구하기 어려운 이유

이 부분이 이해하기 어려웠다. 처음에는 그냥 대충 원함수를 $p(x_i)$로 쓰면 되는거 아닌가? 라는 생각으로 가득했었다. 하지만 아니다. 예시를 들면서 설명하겠다.
$y = x^2$이라는 2차원 식을 [0,2]범위로 몬테카를로 적분을 한다고 쳐보자

Importance Sampling적용을 안한 경우

Importance Sampling 적용을 안한다는 것은 곧 Uniform Distibution을 PDF로 사용한다는 뜻이다. 즉

P(x_i) = 0.5

로 두고 계산하면 된다. PDF로 0.5를 사용하면, N이 작을때는 적분값이 오차가 크지만 N이 커질수록(샘플링을 많이 할수록) 실제 적분값에 점근하게된다.

Importance Sampling적용을 한 경우

Importance Sampling을 적용하기 위해서는 $p(x_i)$를 원함수 $f(x_i)$와 비슷하게 생긴 함수로 채택하면된다. 하지만 PDF는 구간을 적분하면 1이라는 규칙이 있기 때문에

P(x_i) = cx^2

으로 두어야 한다. 여기서 이 c값을 계산하는건 아주 간단하다.
cx^2을 [0,2]에서 정적분해서 1이라는 방정식을 세우면 c값이 3/8으로 구해진다.
그리고 이렇게 구한 $p(x_i)$를 이용해서 샘플링을하면 분산이 0이고 평균이 정확한 적분값인 아주 이상적인 결과가 나온다. 샘플링을 1번만해도 정확한 결과가 나온다.
그런데, 이상한점이 있다. 아주 자연스럽게 $f(x)$의 적분을 구하기 위해 $f(x)$의 적분을 이용해 버렸다는 것이다. 보통 몬테카를로 적분은 렌더링 방정식같이 미적분학을 이용한 적분이 불가능한 case의 적분법이니까 상수 c를 구하는 건 말도 안되는 소리라는 것을 이해할 수 있다.

실제 렌더링 방정식에서의 Importance Sampling

https://computergraphics.stackexchange.com/questions/4979/what-is-importance-sampling
렌더링 방정식은 다음 꼴이다.

적분 연산자 내부에 3개의 함수가 곱해져있다. 이 3개의 함수를 모두 반영한 PDF는 찾기가 쉽지않다. 그러나, 각각을 반영한 PDF는 계산으로 찾아낼수가 있고 실제로 많은 Ray Tracer에서 사용중이다.
예를 들어,

이런 식으로 반구 공간에서의 특정 $\theta$값을 샘플링 하는 방법을 채택할수가 있는것이다.