백준 14865 곡선자르기 (Platinum 5)

전략

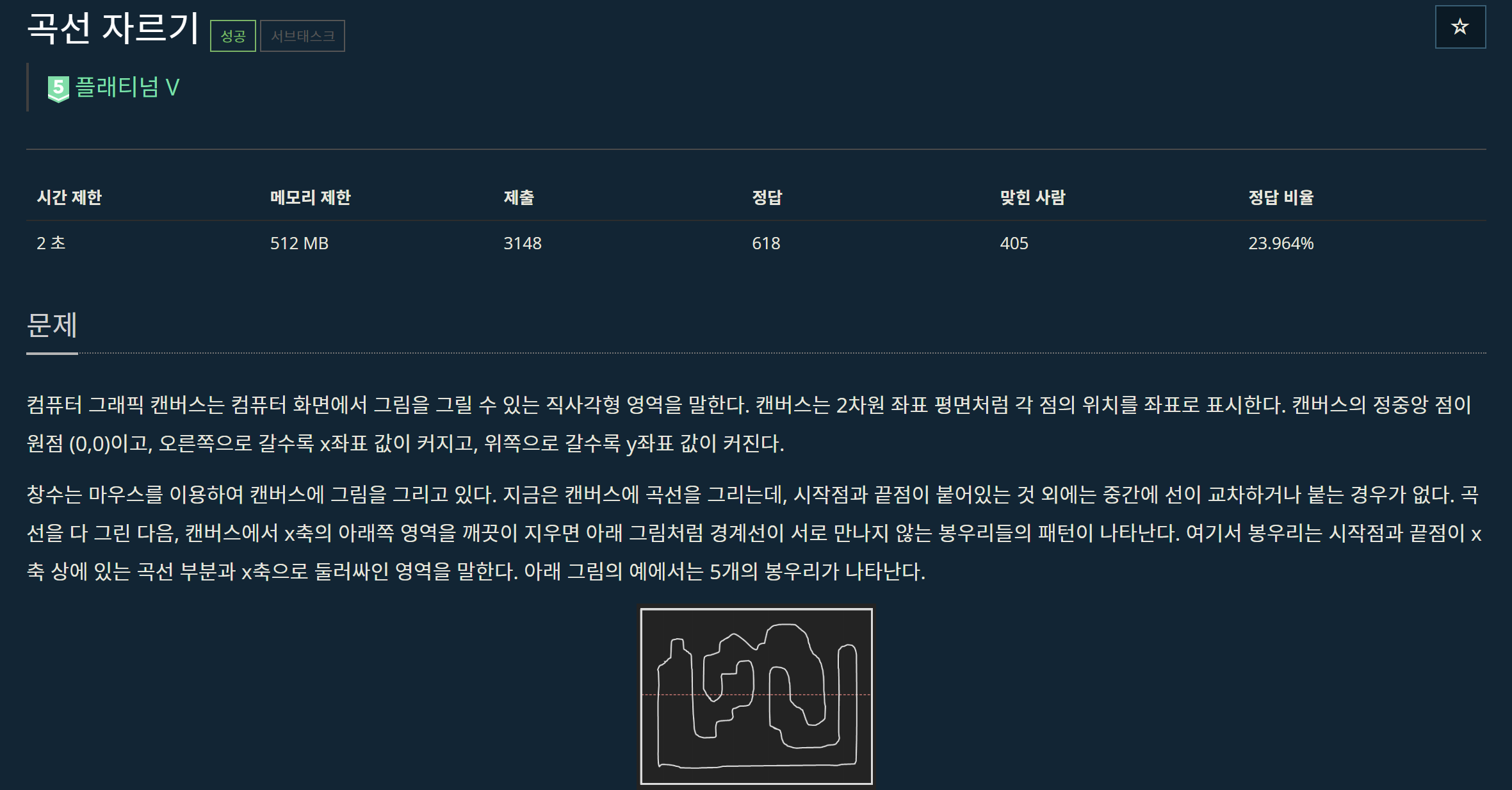
• y = 0인 지점을 기준으로 자르기 떄문에 아래쪽 부분은 신경 쓸 필요가 없다. & 봉우리는 y축 윗쪽에서 생성되고 절댓값이 바뀌는 지점이 시작점 그 직선을 따라 역시 절댓값이 바뀌는 지점이 끝나는 지점이다

• 문제에서 어떤 지점에서 부터 시작하는지 정해져있지 않음 유일하게 정해진 것은 제일 왼쪽 봉우리는 윗쪽으로 올라가는 방향이라는 점

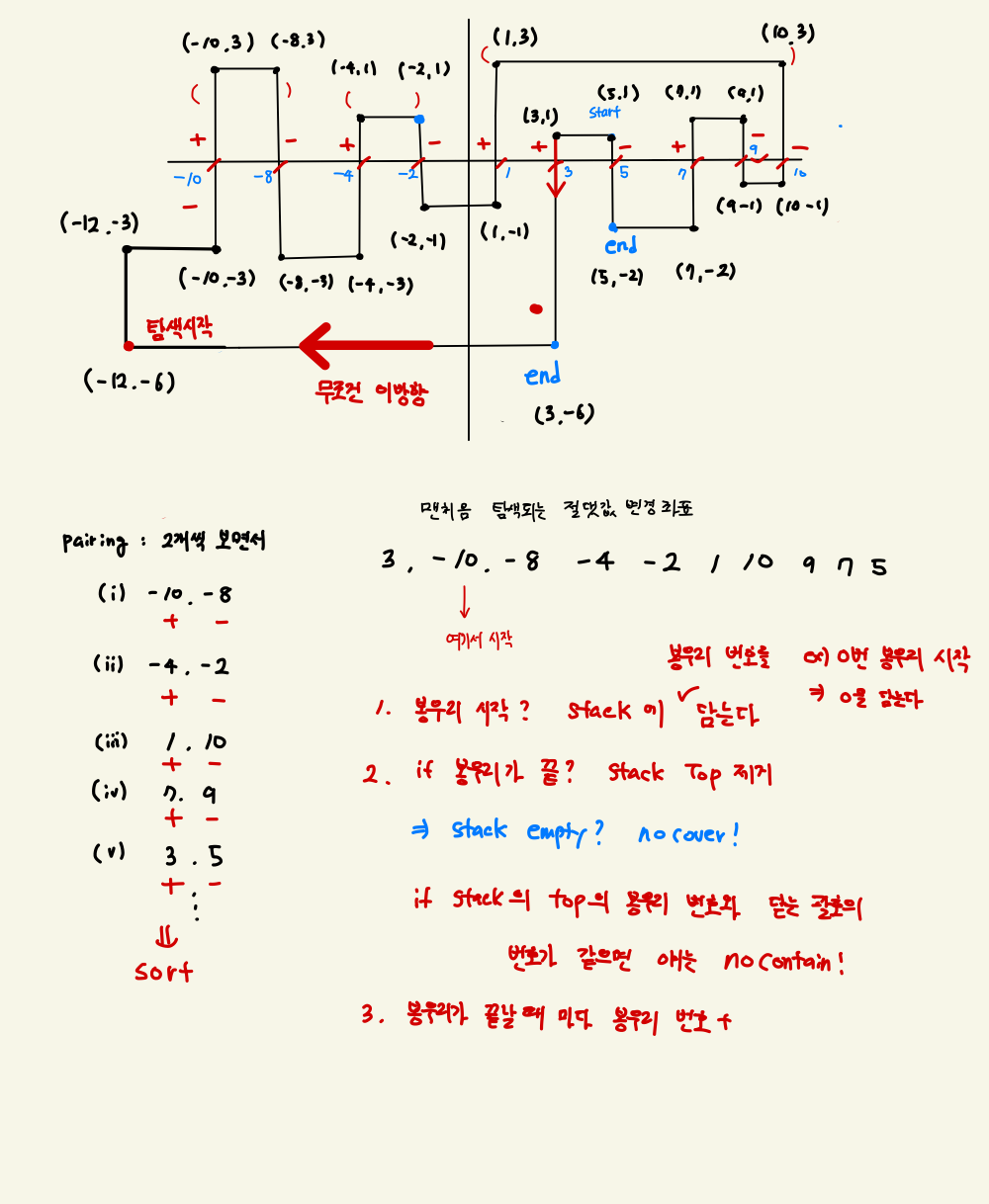
• 입력으로 주어지는 좌표는 서로 연결되어 있기 때문에 문제 조건에 맞는 방향성을 유지하기 위해서 가장 왼쪽 아래에 있는 점부터 시작한다면 가장 먼저 만나는 절댓값의 좌표는 처음 봉우리가 시작되는 좌표이다

• 왼쪽 제일 아래에 있는 좌표부터 시작 index+1씩 늘려가면서 탐색할 좌표와 방향을 고정한다. => 모듈러 연산으로 overflow막기

• 여기서 부턴 2개씩 쌍을 지어서 봉우리의 시작점과 끝이 된다. 왜 why? 연결된 좌표를 줬으니까. 그럼 가장 처음 시작이 음수에서 양수로 넘어가는 값이고 양수로 올라왔을 때 그 다음 절대값이 바뀌는 좌표는 무조건 양수에서 음수로 가는 봉우리다.

• 봉우리 들의 시작점 & 끝점의 모임에서 x값이 작은 값을 시작점 큰 값을 끝 점으로 잡을 거기 때문에 2개씩 페어링 된 x좌표중 x값이 작은 것을 시작점 (isStart = true)를 줘서 구별하게 함

• 모은 봉우리의 시작 & 끝 점들을 정렬한다 만약 서로 다른 봉우리일 떄 1번 봉우리가 끝나기 전에 2번 봉우리가 시작한다면 즉 isStart가 연속해서 나온다면 1번 봉우리가 2번 봉우리를 무조건 포함한다

• 마치 괄호 매칭과 비슷하게 봉우리 객체를 스택에 넣고 isStart를 통해 포함하는 봉우리와 포함되지 않는 봉우리를 구별해서 따로 카운트 해주면 되는 문제

요약 그림

정답코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Stack;

//꼭짓점 클래스
class Point {
	int x;
	int y;
	Point(int x, int y) {
		this.x = x;
		this.y = y;
	}
}

//봉우리 클래스 
class Peak implements Comparable<Peak> {

	int start;
	boolean isStart;

	public Peak(int start, boolean isStart) {
		super();
		this.start = start;
		this.isStart = isStart;
	}

	@Override
	public int compareTo(Peak o) {

		// x값 기준으로 정렬하기
		return this.start - o.start;
	}

}

public class CutCurve {
	static String[] in;
	static int NoContain = 0;
	static int NoCover = 0;

	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int N = Integer.parseInt(br.readLine());
		ArrayList<Point> pointAry = new ArrayList<>();
		ArrayList<Peak> peakAry = new ArrayList<>();
		int StartX = Integer.MAX_VALUE;
		int StartY = Integer.MAX_VALUE;
		int x, y, index = 0;

		for (int i = 0; i < N; i++) {
			in = br.readLine().split(" ");
			x = Integer.parseInt(in[0]);
			y = Integer.parseInt(in[1]);

			// 가장 왼쪽 아래부터 시작한다
			if (x < StartX && y < 0) {
				StartX = x;
				StartY = y;
				index = i;
			}

			Point p = new Point(x, y);
			pointAry.add(p);
		}

		int prevX = StartX;
		int prevY = StartY;
		int len = pointAry.size();

		// 왼쪽 제일 아래부터 탐색한다. but 중간에 있을 수도 있으니까 모듈러 연산 이용
		for (int i = 0; i < len; i++) {
			Point nowPoint = pointAry.get((index + i) % len);

			// 이전 y가 음수 현재 y가 양수일 때 -> 시작하는 봉우리
			if (prevY < 0 && nowPoint.y > 0) {

				// 이전 관통 선분이 봉우리 끝이면 지금 관통 선분은 무조건 봉우리 시작부분이다
				prevX = nowPoint.x;
				prevY = nowPoint.y;
			}

			// 봉우리가 끝나는 지점일 때 업데이트 해준다
			else if (prevY > 0 && nowPoint.y < 0) {
				int minX = Math.min(prevX, nowPoint.x);
				int maxX = Math.max(prevX, nowPoint.x);

				prevX = nowPoint.x;
				prevY = nowPoint.y;

				Peak left = new Peak(minX, true);
				Peak right = new Peak(maxX, false);
				peakAry.add(left);
				peakAry.add(right);
			}
		}

		// 커지는 순서로 봉우리를 정렬한다
		Collections.sort(peakAry);

		// 봉우리를 담는 스택
		Stack<Integer> peakStack = new Stack<>();
		int lenAry = peakAry.size();
		int numPeak = 0;

		for (int i = 0; i < lenAry; i++) {
			boolean check = peakAry.get(i).isStart;

			// 만약 봉우리가 시작하는 변이라면 스택에 담는다
			if (check == true) {
				peakStack.add(numPeak);
			}

			// 만약 봉우리가 끝나는 변이라면
			else {
				// stack의 가장 윗부분을 빼주고
				int left = peakStack.pop();

				// 만약 스택이 비워져 있다면 얘는 noCover이다
				if (peakStack.isEmpty()) {
					NoCover++;
				}

				// 만약 스택이 차있고 왼쪽 괄호 바로 다음에 오른쪽 괄호가 오는 경우는 NoContain (( )경우
				// 포함은 되어있지만 포함하지는 않는다
				if (left == numPeak) {
					NoContain++;
				}

				// 아닌 경우엔 포함되어 있으면서 포함도 한다
				// 시작하는 봉우리를 만날 때 마다 봉우리 갯수를 늘려준다
				numPeak++;
			}

		}

		System.out.println(NoCover + " " + NoContain);
	}

}