백준 2887 행성 터널 (Platinum 5)

전략

https://www.acmicpc.net/problem/4386

위 링크에 있는 별자리 만들기와 유사한 문제지만 좌표의 범위와 연결하는 조건이 다른 문제

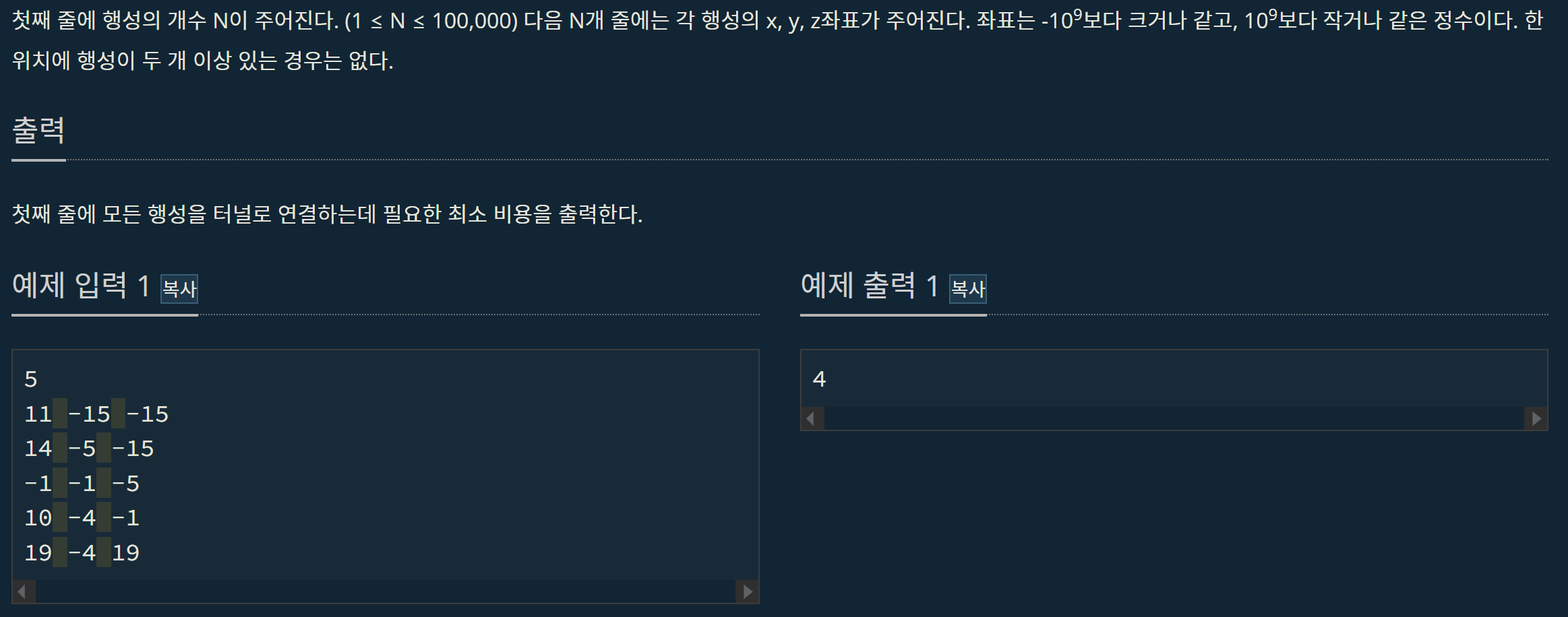
• 각각의 행성을 좌표에 따라 모든 행성을 연결하는 최소 길이를 구하는 문제

  • 최소 신장 트리 문제로 크루스칼 알고리즘을 적용해야하는 문제

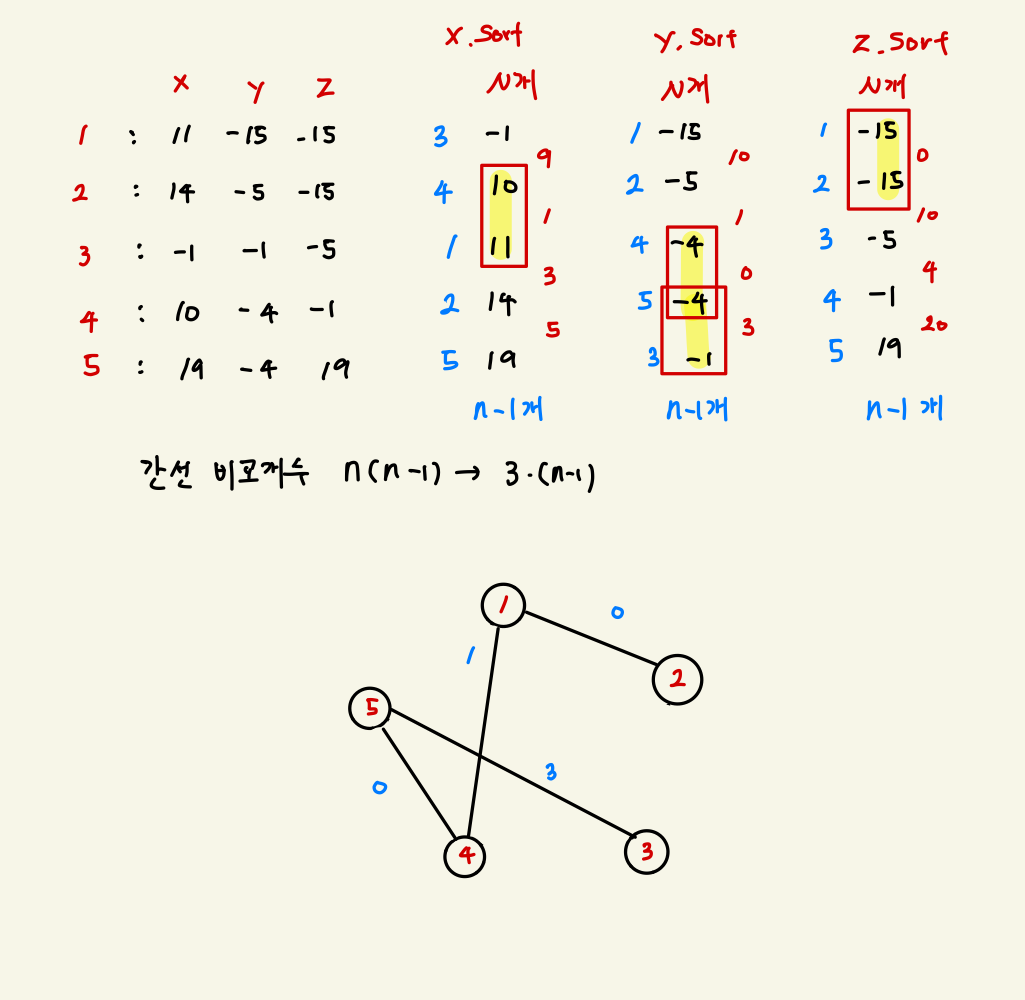
• Update Rule은 x, y, z 좌표중에 min값으로 거리가 결정된다

• 만약에 모든 N개의 별에 대해서 다른 별들과의 거리를 다 구해서 정렬한 후 MST를 찾고자 하면 O(N^2)이 나와서 시간초과가 발생한다.

• 사용한 아이디어: 어차피 x,y,z 중 가장 작은 값이 연결되니까 별 번호만 기억하고 x,y,z를 분리해서 각각 거리가 최소인 별들끼리 연결하자. 만약에 x,y,z의 차이가 다른 경우 어차피 나중엔 별 정보와 간선 무게만 저장되기 때문에 굳이 x,y,z를 구별할 필요가 없다

• 즉 N(N-1)번 비교해야하는 거에서 3(N-1)번만 비교하면 되는 문제

• 이후에 총 합을 구하는 알고리즘은 기본적인 크루스칼 알고리즘을 사용한 MST를 구하는 문제와 동일하다

정답코드

package algorithms;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.StringTokenizer;

class StarInfo implements Comparable<StarInfo> {

	int starNum;
	int value;

	public StarInfo(int starNum, int value) {
		this.starNum = starNum;
		this.value = value;
	}

	@Override
	public int compareTo(StarInfo o) {
		return this.value - o.value;
	}
}

class StarEdge implements Comparable<StarEdge> {
	int start;
	int end;
	int Value;

	public StarEdge(int start, int end, int Value) {
		this.start = start;
		this.end = end;
		this.Value = Value;
	}

	@Override
	public int compareTo(StarEdge o) {
		return this.Value - o.Value;
	}
}

public class PlanetTunnel {

	static int[] parent;
	static int N;
	static ArrayList<StarInfo> tempXList;
	static ArrayList<StarInfo> tempYList;
	static ArrayList<StarInfo> tempZList;
	static ArrayList<StarEdge> StarEdgeInfo;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		N = Integer.parseInt(st.nextToken());

		tempXList = new ArrayList<>();
		tempYList = new ArrayList<>();
		tempZList = new ArrayList<>();
		StarEdgeInfo = new ArrayList<>();
		parent = new int[N];

		// 루트노드 초기화
		for (int i = 0; i < N; i++) {
			parent[i] = i;
		}
		
		//별 번호 i와 각각에 해당하는 x값, y값, z값에 대응하는 객체를 만들기 
		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine());
			int xVal = Integer.parseInt(st.nextToken());
			int yVal = Integer.parseInt(st.nextToken());
			int zVal = Integer.parseInt(st.nextToken());

			StarInfo x = new StarInfo(i, xVal);
			StarInfo y = new StarInfo(i, yVal);
			StarInfo z = new StarInfo(i, zVal);

			tempXList.add(x);
			tempYList.add(y);
			tempZList.add(z);
		}

		// 좌표 별로 정렬
		Collections.sort(tempXList);
		Collections.sort(tempYList);
		Collections.sort(tempZList);

		int prev = tempXList.get(0).starNum;
		int prevGrid = tempXList.get(0).value;

		//x값이 작은 것 부터 정렬된 자료로 부터 인접한 별들끼리의 거리를 구해서 전체 리스트에 넣는다 
		for (int i = 1; i < N; i++) {
			int next = tempXList.get(i).starNum;
			int nextGrid = tempXList.get(i).value;
			int weight = nextGrid - prevGrid;

			StarEdge star = new StarEdge(prev, next, weight);
			StarEdgeInfo.add(star);
			prev = next;
			prevGrid = nextGrid;
		}

		prev = tempYList.get(0).starNum;
		prevGrid = tempYList.get(0).value;
		
		//y값이 작은 것 부터 정렬된 자료로 부터 인접한 별들끼리의 거리를 구해서 전체 리스트에 넣는다 
		for (int i = 1; i < N; i++) {
			int next = tempYList.get(i).starNum;
			int nextGrid = tempYList.get(i).value;
			int weight = nextGrid - prevGrid;

			StarEdge star = new StarEdge(prev, next, weight);
			StarEdgeInfo.add(star);

			prev = next;
			prevGrid = nextGrid;
		}

		prev = tempZList.get(0).starNum;
		prevGrid = tempZList.get(0).value;

		//z값이 작은 것 부터 정렬된 자료로 부터 인접한 별들끼리의 거리를 구해서 전체 리스트에 넣는다 
		for (int i = 1; i < N; i++) {
			int next = tempZList.get(i).starNum;
			int nextGrid = tempZList.get(i).value;
			int weight = nextGrid - prevGrid;

			StarEdge star = new StarEdge(prev, next, weight);
			StarEdgeInfo.add(star);
			prev = next;
			prevGrid = nextGrid;
		}
		
		//각각의 간선 weight를 가진 점들을 정렬한다
		Collections.sort(StarEdgeInfo);
		
		//간선의 크기가 작은 것 부터 이미 연결된 집합인지 확인
		//만약 연결되지 않았다면 union해주고 간선의 총합을 더해준다 
		int cnt = 0;
		int total = 0;
		for (int i = 0; i < StarEdgeInfo.size(); i++) {
			StarEdge star = StarEdgeInfo.get(i);
			// 둘이 연결 된 적 없다면
			if (!equals(find(star.start), find(star.end))) {
				union(star.start, star.end);
				total += star.Value;
				cnt++;
			}
			if(cnt == N-1)break;
		}

		System.out.println(total);
	}

	// a,b의 대소관계에 따라서 부모노드를 바꿔준다
	public static void union(int a, int b) {
		// 최상위 부모 찾기
		int x = find(a);
		int y = find(b);

		if (x < y) {
			parent[y] = x;
		} else {
			parent[x] = y;
		}
	}

	// a와 b의 부모가 같은지 확인
	public static boolean equals(int a, int b) {
		int x = find(a);
		int y = find(b);
		return x == y;
	}

	// a의 부모노드를 찾는 연산
	public static int find(int a) {
		if (parent[a] == a)
			return a;
		return parent[a] = find(parent[a]);
	}
}