백준 16566 카드게임(Platinum5)

전략

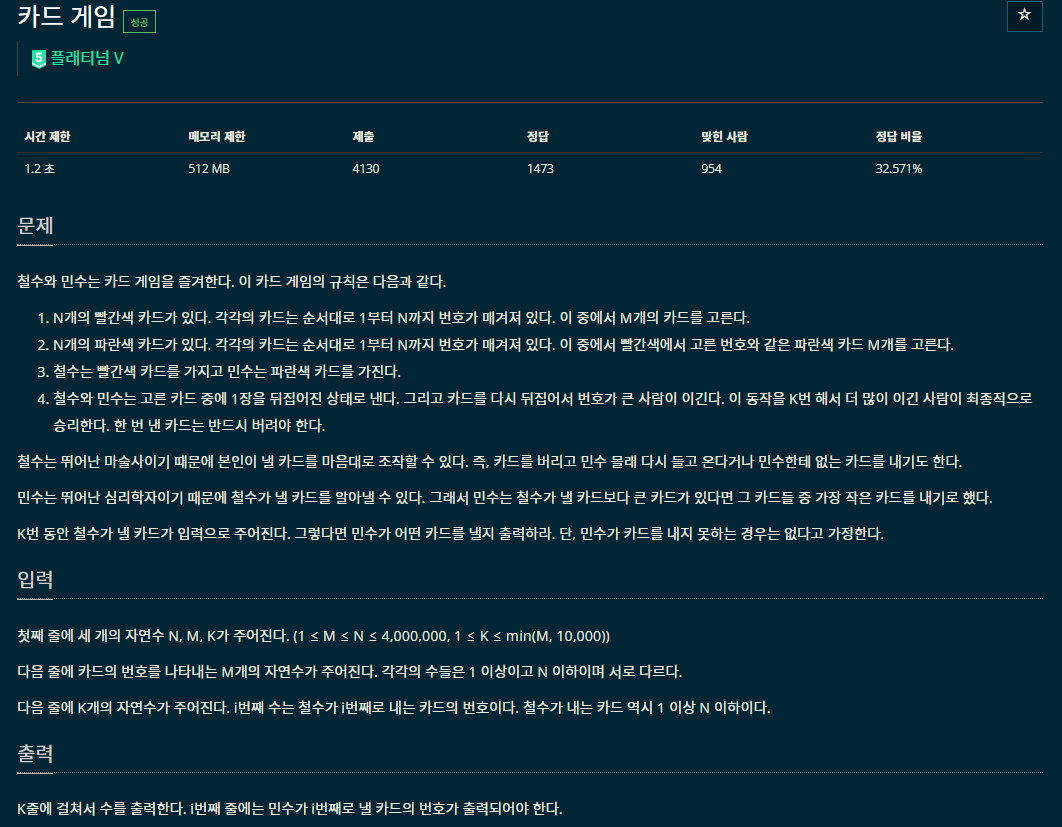
• 철수와 민수는 같은 카드 번호를 가지고 있고 철수는 이미 내버린 카드도, 민수가 없는 카드도 낼 수 있기 때문에 모든 카드의 조합을 낼 수 있다(중복 가능)

• 민수는 철수가 낸 카드보다 큰 숫자들 중에 가장 작은 원소를 내야한다.

• 여기서 N,M = 4*10^6 이고 게임횟수가 10^4이기 때문에 O(MK)으로 코드를 작성하게 되면 시간초과가 발생한다 -> 최대 O(KlogM)의 코드가 되도록 작성해야함

1. 뽑은 M개의 카드를 쌩정렬이 아니라 Counting sort를 이용하여 O(M)에 정렬하여 0~N 개의 false로 초기화된 배열에 뽑은 카드는 true 표시를 해준다

2. 한번 더 순회하면서 true이면 그 카드의 인덱스를 순서대로 담아주면 M개의 카드를 2*M으로 정렬이 가능하다.

3. 철수가 낸 카드 번호에 대해서 이분탐색으로 민수가 낼 수 있는 카드를 구한다 KlogM에 가능

4. 만약 이걸 일반 배열에 대해서 수행한다면 값을 삭제하고 배열을 재조정하는 과정에서 M의 시간이 들기 때문에 총 KMlogM으로 시간초과가 발생한다

5. 그에 대한 해결방안으로 유니온-파인드를 이용한다. 만약 철수의 카드에 대해서 뽑을 카드를 정했다면 그 카드와 그 다음 인덱스에 있는 카드를 유니온 해준다

6. 이때 큰 쪽으로 노드를 합쳐줘야 이전 인덱스로 find 요청이 들어왔을 때 노드를 타고 제일 끝에 있는(인덱스가 가장 큰) 노드 값으로 들어온다

정답코드

package algo2;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class CardGame {
	static int N;
	static int M;
	static int K;
	static int[] baseCard;
	static boolean[] pickedCard;
	static int[] cardList;
	static int[] parent;
	static StringBuilder sb = new StringBuilder();
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		K = Integer.parseInt(st.nextToken());
		
		//N개의 카드 중에서 어떤 M개의 카드가 뽑혔는지 확인하는 부울 배열
		pickedCard = new boolean[N+1];
		//뽑은 M개의 카드들이 저장되어있는 리스트
		cardList = new int[M];
		//철수가 뽑은 카드들
		baseCard = new int[K];
		//부모노드 초기화 
		parent = new int[M];
		
		for(int i = 0; i < M; i++) {
			parent[i] = i;
		}
		
		
		st = new StringTokenizer(br.readLine());
		for(int i = 0; i < M; i++) {
			int now = Integer.parseInt(st.nextToken());
			pickedCard[now] = true;
		}
		
		st = new StringTokenizer(br.readLine());
		for(int i = 0; i < K; i++) {
			int now = Integer.parseInt(st.nextToken());
			baseCard[i] = now;
		}
		
		//O(M)을 이용한 counting sort
		int c = 0;
		for(int i = 0; i < N+1; i++) {
			if(pickedCard[i]==true) {
				cardList[c] = i;
				c++;
			}
		}
		
        //정렬된 카드리스트에서 시작한다
		for(int i = 0; i < K; i++) {
			int nowCard = baseCard[i];
			int idx = binarySearch(nowCard); //해당카드가 있는 index 찾기
			idx = find(idx); //현재 idx의 루트 노드 찾기
			
			sb.append(cardList[idx]);
			sb.append('\n');
			
            //맨 끝에 인덱스 제외하고 현재 고른 idx 정보와 idx+1를 유니온
			if(idx!=M-1)union(idx, idx+1);
		}

		System.out.println(sb);
	}
	
	//이분탐색으로 값 찾기 
	public static int binarySearch(int target) {
		
		int left = 0;
		int right = M - 1;
		int mid;
		
		while(left<right) {
			mid = (left+right)/2;
			if(cardList[mid]<target)left = mid+1;
			else if(cardList[mid]>target)right = mid;
			//값을 찾은 경우 그 인덱스의 다음 값을 넘겨준다
            //why 4가 나왔을 때 4가 아닌 그 다음 인덱스 카드를 내야함 
			else return mid+1;
		}
		//똑같은 카드가 없으면 해당 인덱스 리턴하면 그 카드보다 한 단계 큰 카드
		return left;
	}
	
    //a,b의 대소관계에 따라서 부모노드를 바꿔준다 
    public static void union(int a, int b) {
        // 최상위 부모 찾기
        int x = find(a);
        int y = find(b);
        
        //여기서 index가 큰 쪽으로 부모를 합쳐줘야 한다
        if (x > y) {
            parent[y] = x;
        } else {
            parent[x] = y;
        }
    }
    
    //a의 부모노드를 찾는 연산 
    public static int find(int a) {
        if (parent[a] == a)
            return a;
        return parent[a] = find(parent[a]);
    }

}