Convex Hull

난1렙이요·2024년 10월 23일

알고리즘

목록 보기

10/15

Convex Hull

convex hull은 좌표평면과 도형에 관련한 문제이다. 좌표평면에서 여러가지 점들이 있을 때, 이 점들을 모두 포함하면서 크기(블록)가 제일 작은 도형을 만드는 문제이다.
이 문제는 점들을 정렬하는 과정이 필요하기에 $O(nlogn)$ 보다 빠를 수 없다.

점들이 이렇게 위치해있다고 하자. 이 때 Convex Hull은 제일 바깥쪽에 있는 점들을 모아 연결한 도형이다.

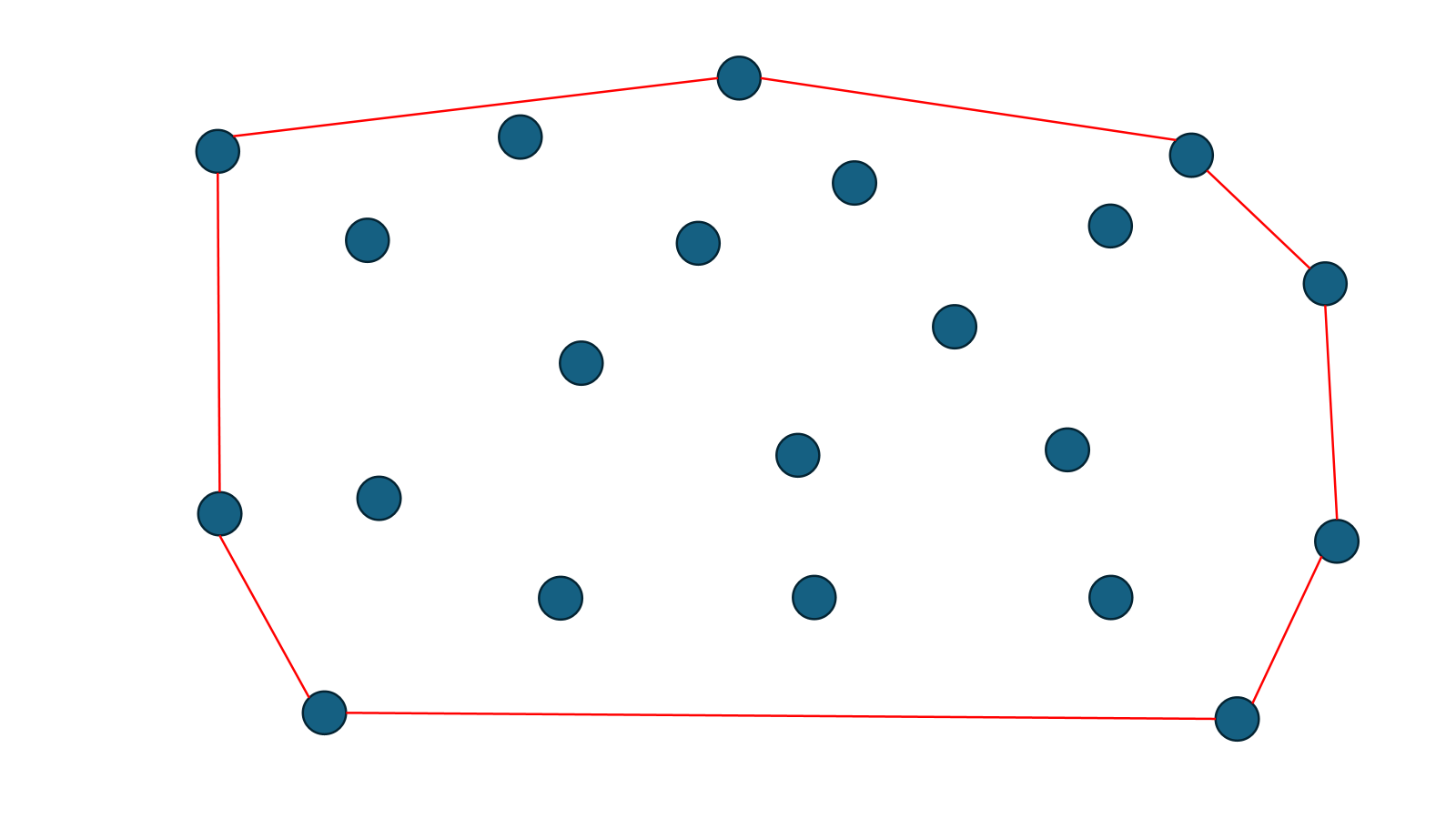
그러므로 이러한 모양이 된다.

Convex Hull을 파악하기 전 알아두면 좋은 요소가 있는데, CCW이다.

CCW(Counter-Clock-Wise)

CCW는 점 3개를 연결하여 좌회전하는지, 우회전하는지를 파악하는 방법이다.

3점의 위치가 주어진다.
각각은 $p,q,r$ 이다.
$p$ 에서 $q$ 를 거쳐 $r$ 로 갈 때, 좌회전을 하는지 우회전을 하는지를 판별할 수 있는가?
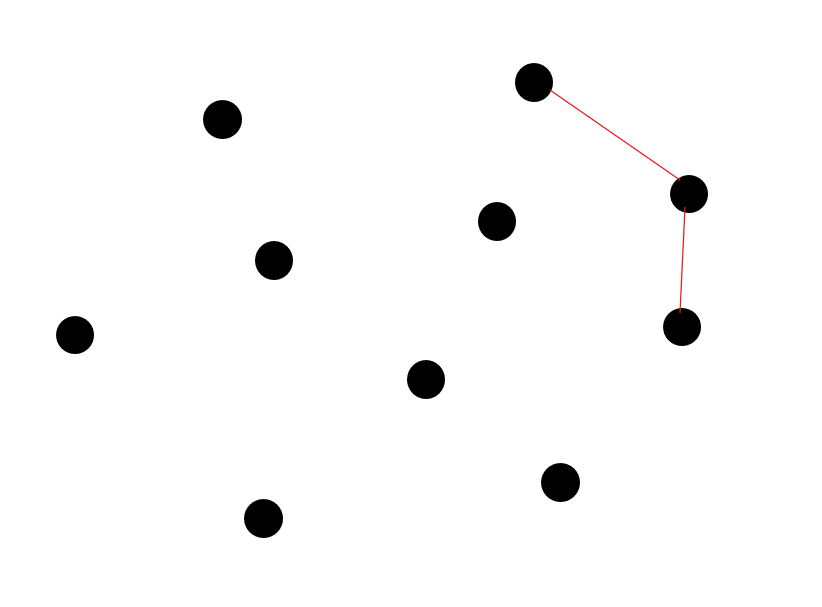
$\frac{y_{2}-y_{1}}{x_{2}-x_{1}} > \frac{y_{3}-y_{2}}{x_{3}-x_{2}}$ 면 우회전
$\frac{y_{2}-y_{1}}{x_{2}-x_{1}} < \frac{y_{3}-y_{2}}{x_{3}-x_{2}}$ 면 좌회전

Brute-Force-Ish

$O(n^3)$ 의 방법. 모든 점에 대해서 $p,q,r$ 을 지정해서 좌회전인지 우회전인지 확인함.

점 $p$ 와 $q$ 에 대해서 어떠한 점 $r$ 을 뽑고 CCW를 했을 때 모두 우회전이므로 $p-q$ 는 Convex Hull의 경계선에 있다.

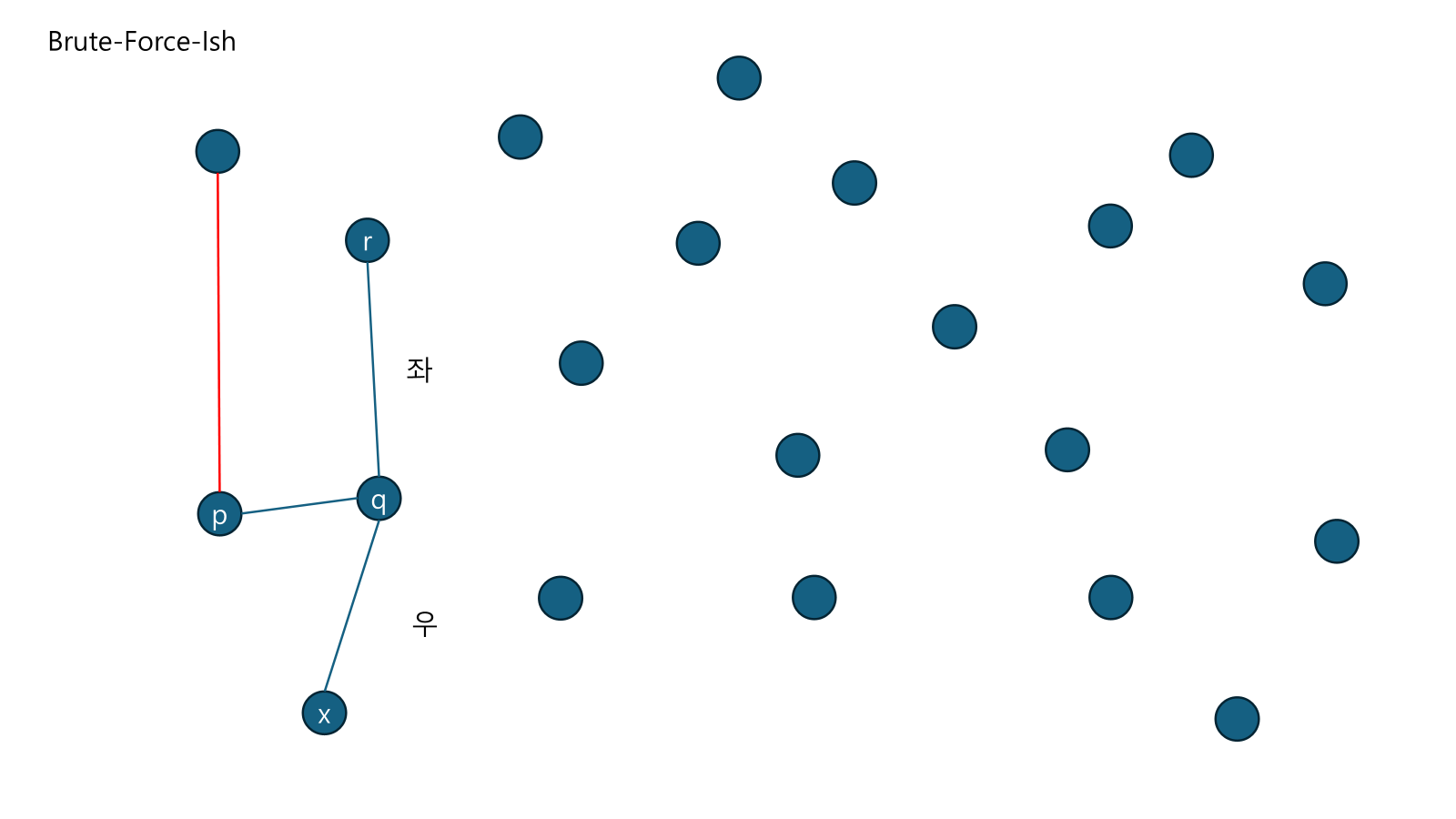
점 $p$ 와 $q$ 에 대해서 $r$ 을 뽑고 CCW를 했을 때는 좌회전이고, $x$ 를 뽑고 CCW를 했을 때는 우회전이므로 Convex Hull의 경계선에 있지 않다.

점 $p$ 를 뽑음
점 $q$ 를 뽑음
점 $p$ 와 $q$ 를 뺀 모든 나머지 점 $r$ 에 대해서 CCW를 함
- 맨 처음에 한 CCW의 상태를 $S_1$ 라 함
- 만약 $S_i \neq S_1$ 면 break함.
- 모든 $S_i$ 가 $S_1$ 이면 $p$ 와 $q$ 를 Convex Hull의 경계선에 추가시킴
모든 점에 대해서 반복
모든 점에 대해서 반복을 완료했으면 종료

점 $p$ 는 $n$ 번 뽑으며, 점 $q$ 는 $n-1$ 번 뽑음. 점 $r$ 은 최대 $n-2$ 번 뽑으므로 $O(n^3)$ 이 걸림.

Package wrapping

$O(n^2)$ 의 방법.

Convex Hull의 경계선에 포함되어 있는게 보장되는 점 (ex.제일 오른쪽에 있는 점 )하나를 $p$ 로 잡음.
$p$ 의 바로 옆에 있는 점을 $q$ 로 잡음
$p,q$ 가 아닌 모든 임의의 점 $r$ 과 CCW를 수행
- 맨 처음에 한 CCW의 상태를 $S_1$ 라 함
- 만약 $S_i \neq S_1$ 면 break함.
- 모든 $S_i$ 가 $S_1$ 이면 $p$ 와 $q$ 를 Convex Hull의 경계선에 추가시킴
- 점 $q$ 를 점 $p$ 로 바꿈
만약 옆에 있는 점 $q$ 가 CCW의 한 방향을 모두 만족하지 않는다면 $q$ 의 옆에 있는 점을 $q$ 로 바꾸고 다시 알고리즘을 수행
반복
처음에 들어온 점이 다시 들어오면 알고리즘 종료

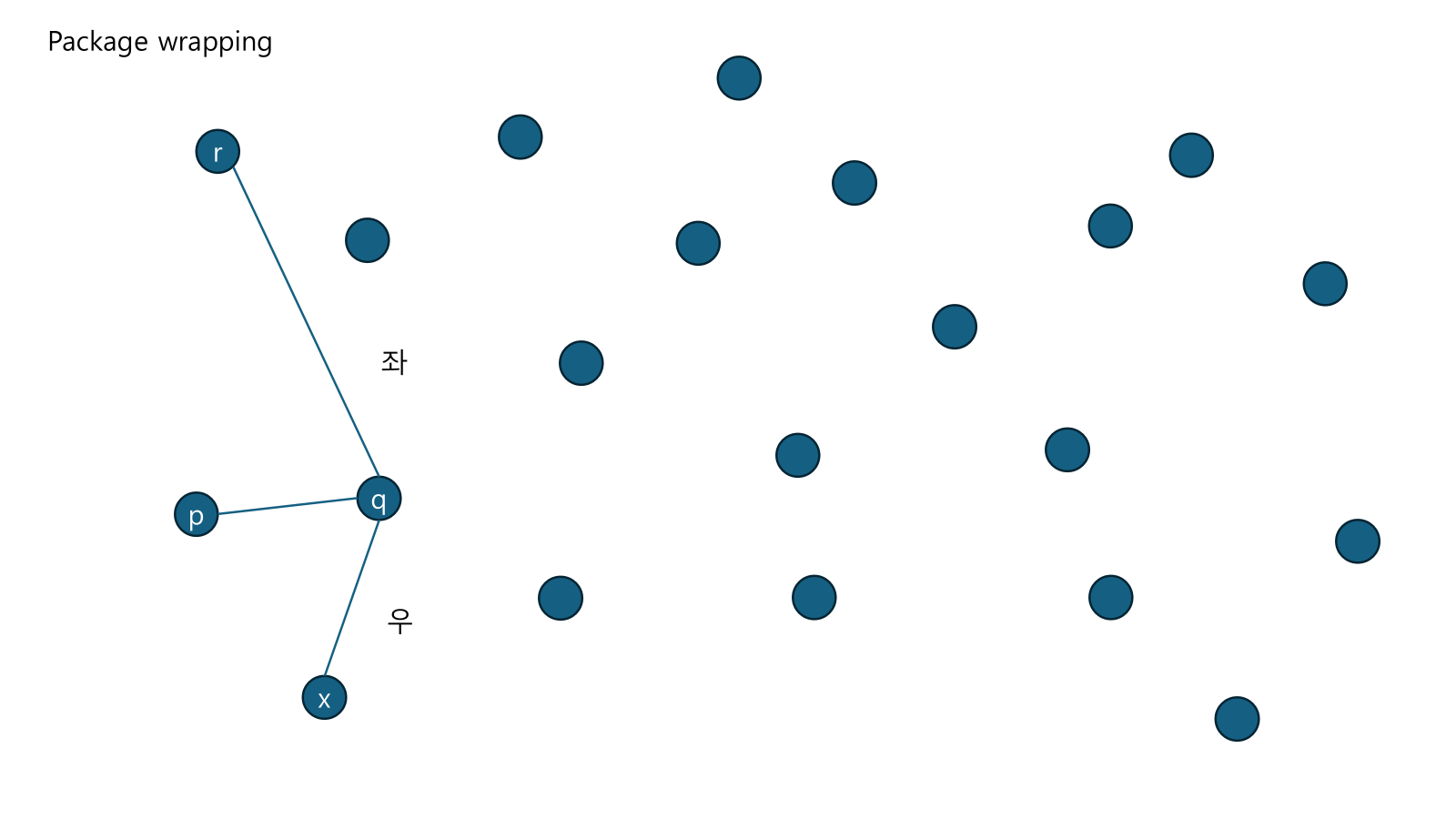
$p$ 의 바로 위에 있는 점 $q$ 가 조건을 만족하지 않음. 이런 경우 $q$ 의 위쪽 점을 $q$ 로 바꾸며 이어감

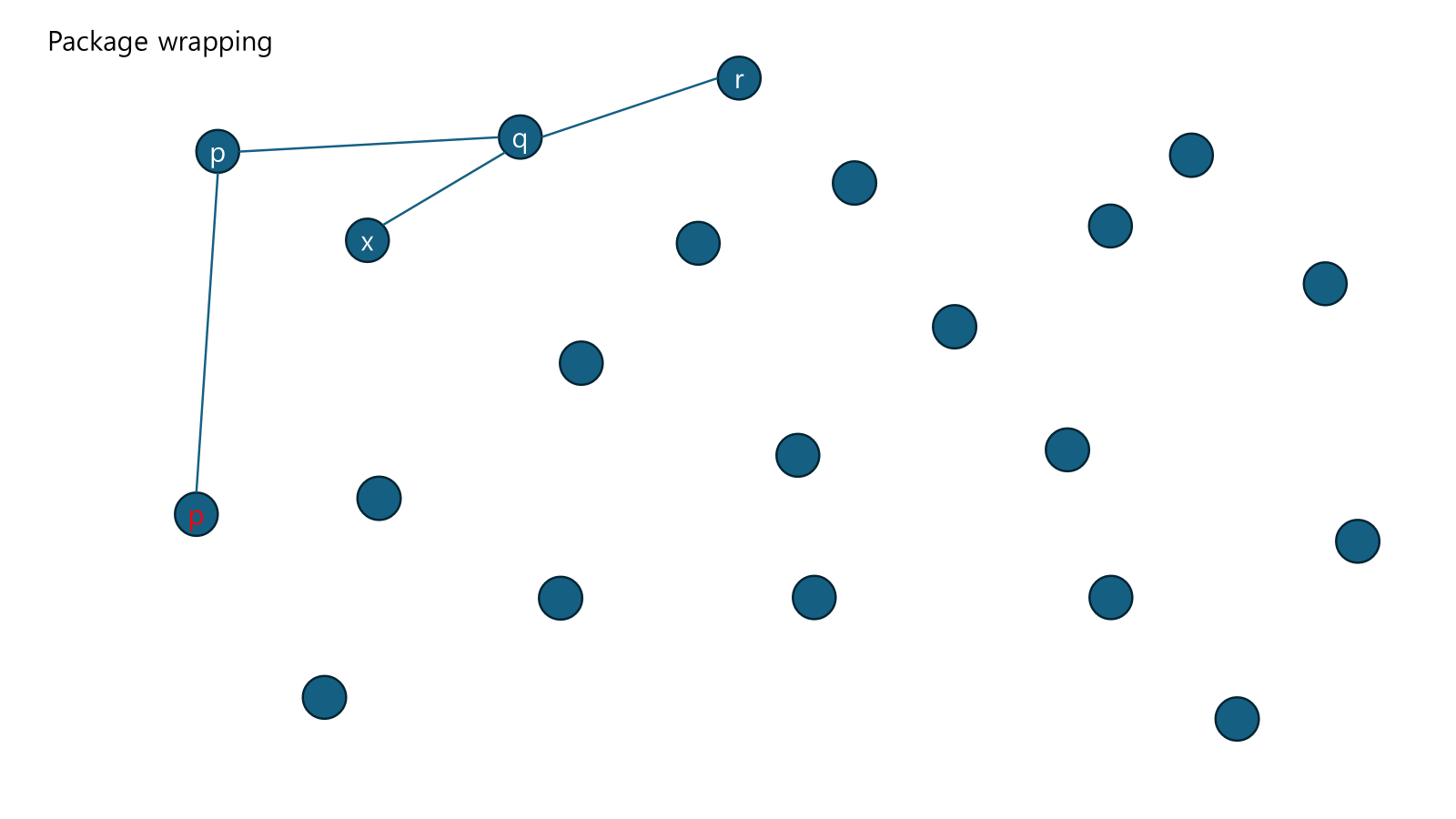
만족하는 $q$ 를 찾았으면 $q$ 를 $p$ 로 바꾸고 알고리즘이 종료할 때 까지 수행함.

Graham Scan

$O(nlogn)$ 의 방법. 각도를 기준으로 정렬하고 Stack에 점들을 넣어 만드는 방법이다.

점 하나를 잡음
각도를 작은 것부터 정렬함 $O(nlogn)$
들어올 점 x에 대해서 이미 도형에 포함된 점 x-1과 x-2를 기준으로 CCW를 함.
- 만약 우회전(좌회전)이면 x-1을 pop하고
- 만약 좌회전(우회전)이면 x를 push함
Convex Hull이 만들어질 때까지 반복

우회전과 좌회전은 바꾸어도 차이가 없지만, 한 방향으로 탐색하기로 결정했으면 계속 그 방향으로 해야함.

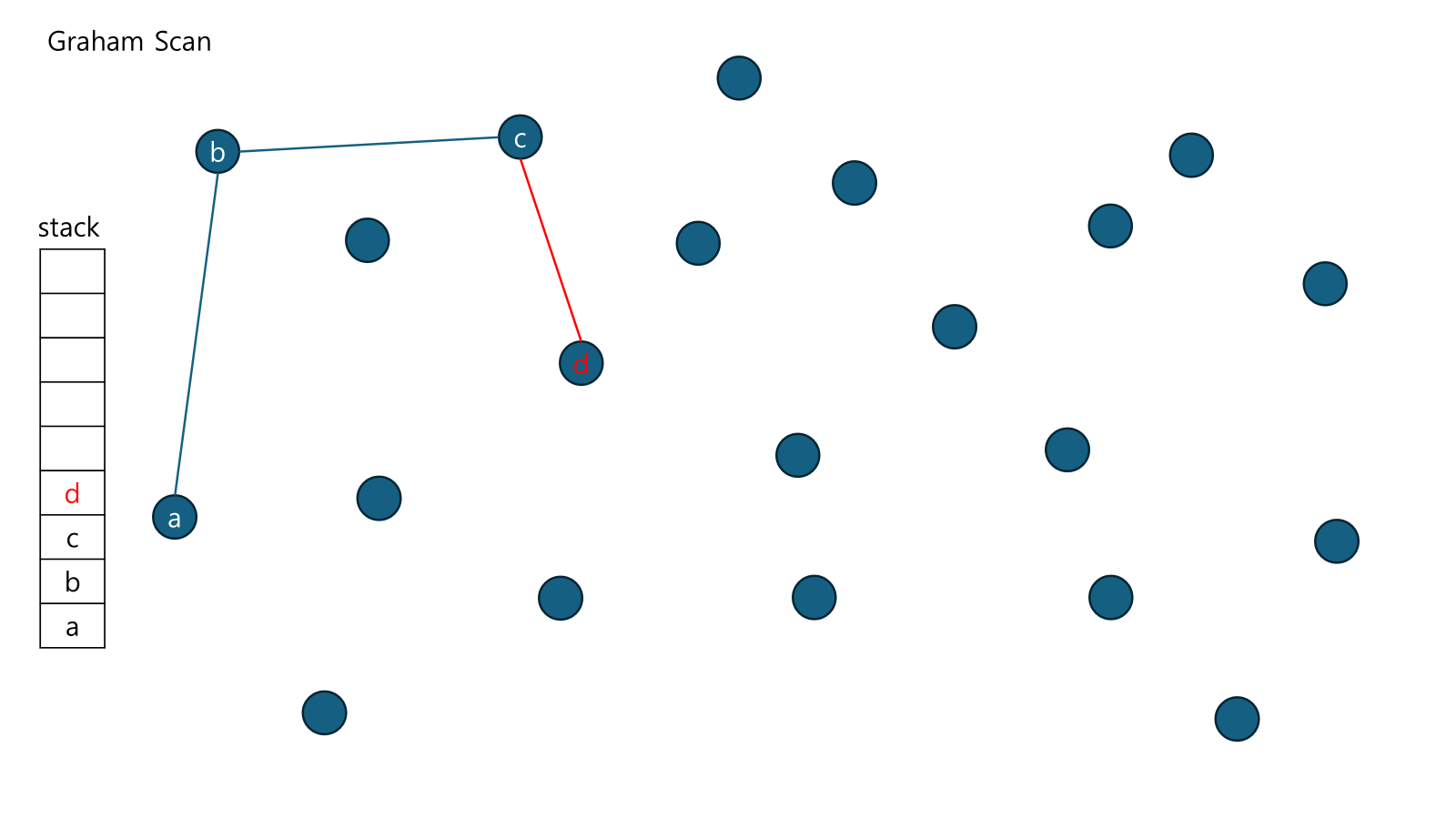
Graham Scan이 어느정도 진행 된 상태임.

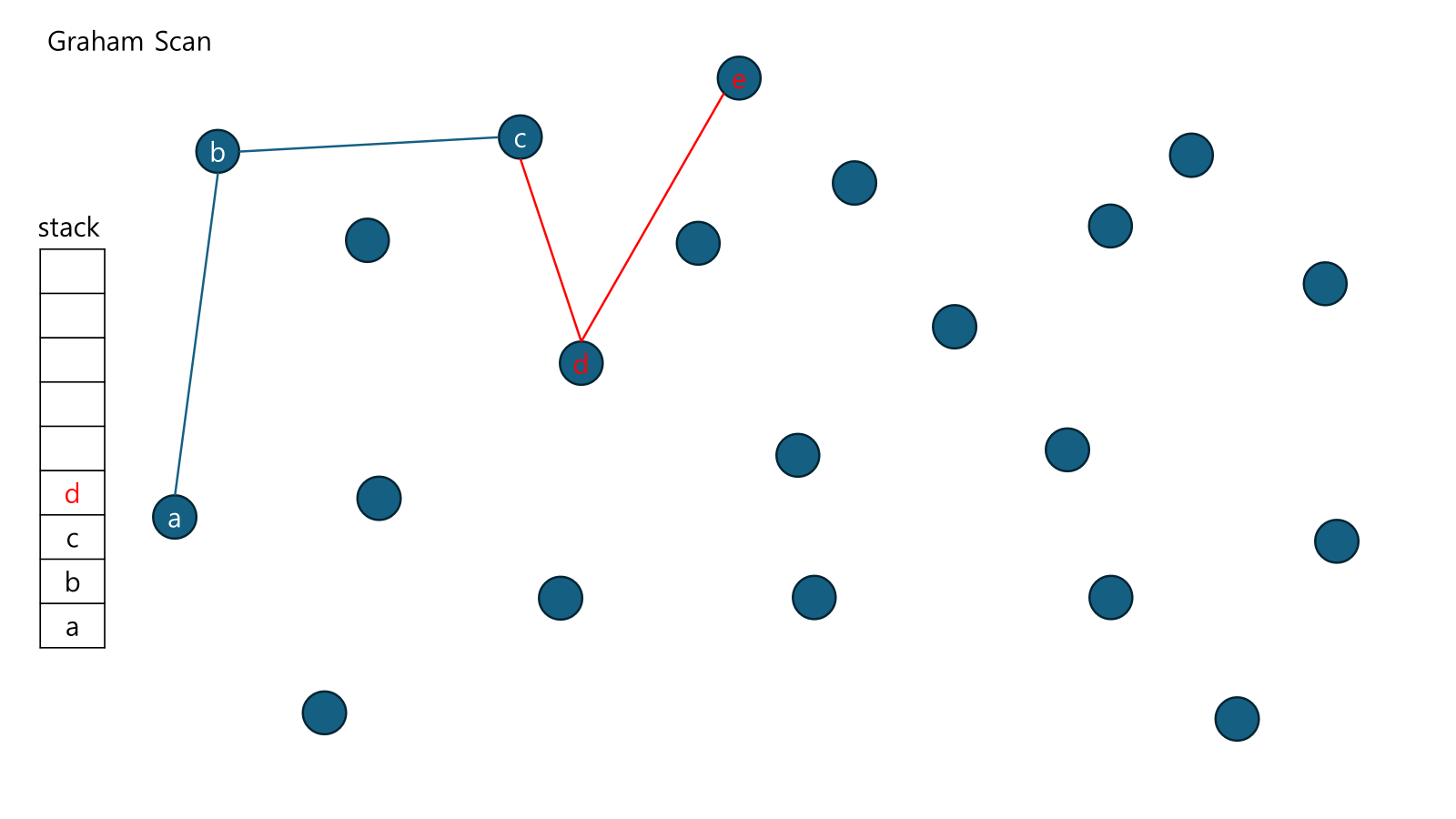
이 때 점 e가 (인위적으로) 들어옴. e-d-c의 CCW는 좌회전이므로 우리가 우회전으로 탐색한 것과 반대됨.

d를 pop하고 e-c-b를 CCW함. 똑같이 좌회전이므로 우리가 우회전으로 탐색한 것과 반대됨.

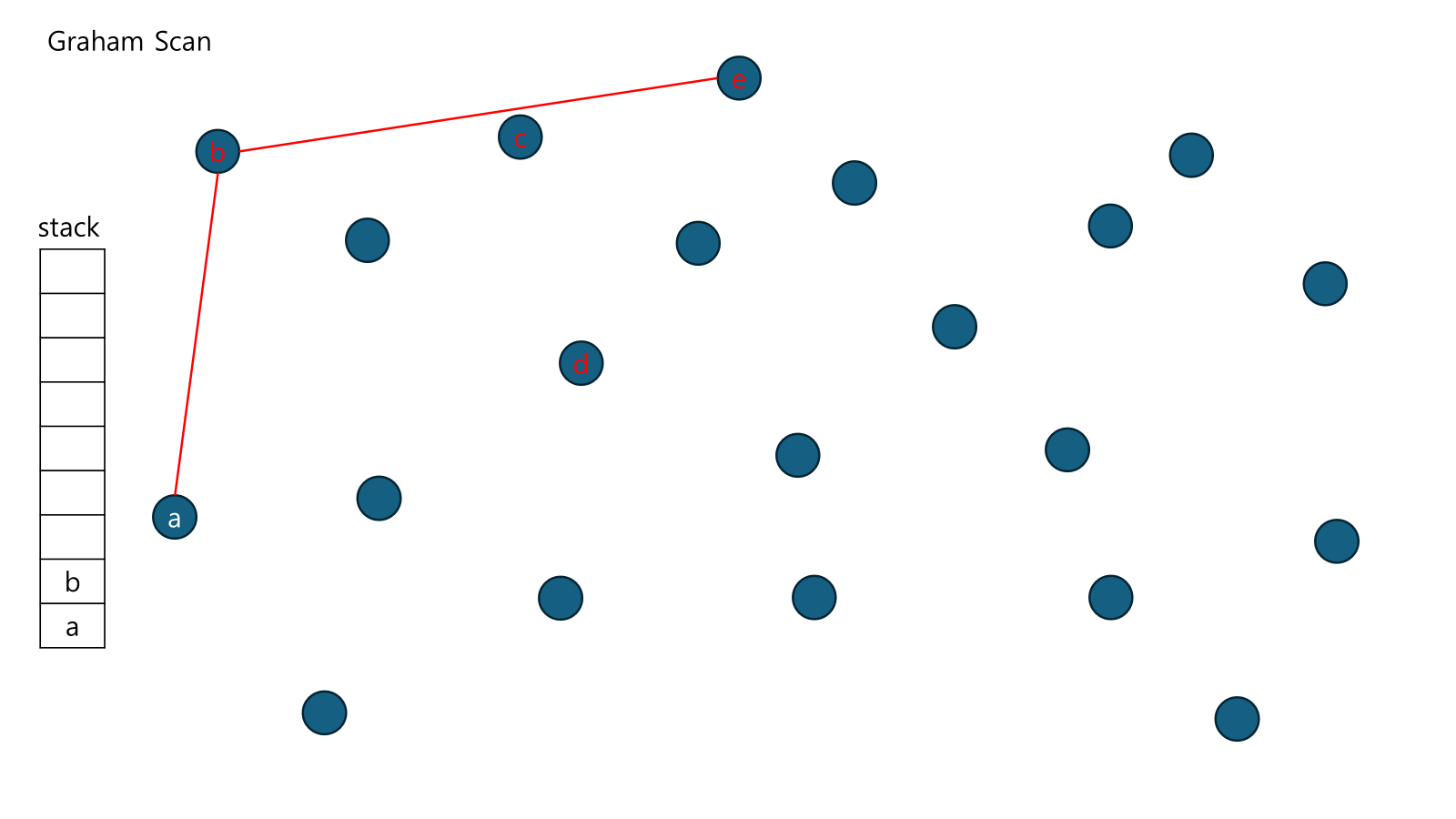
c를 pop하고 e-b-a를 CCW함. 우회전이므로 조건을 만족함.

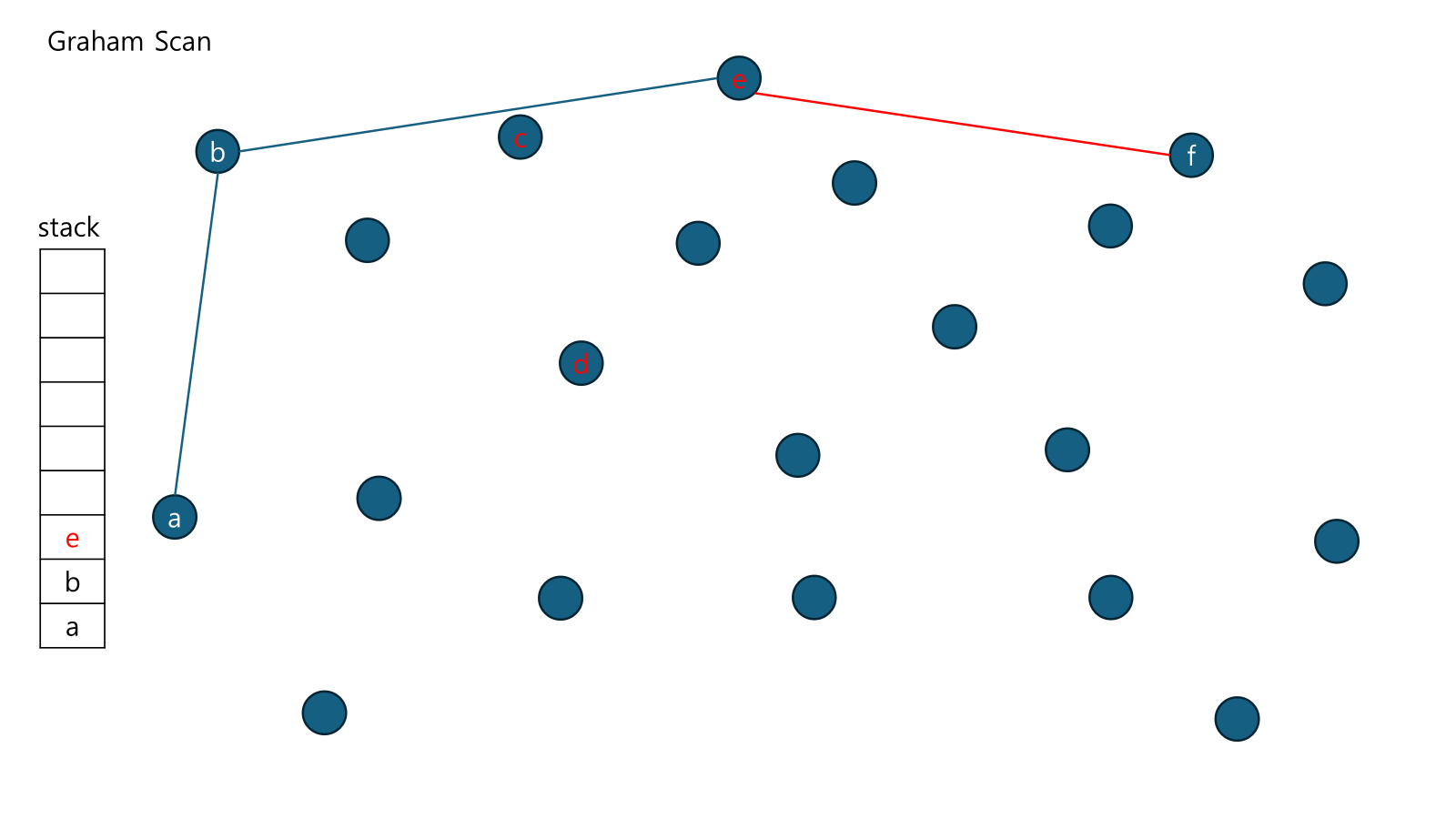
e를 push하고 다음 점 f에 대해서 f-e-b를 수행... 반복함

$O(nlogn)$

Plain Sweeping

$O(nlogn)$ . 접선을 이용하는 방법이다.

Right Hull에 대해서 설명한다.
Right Hull의 맨 끝 점 바로 옆에 점을 $x$ 로 잡는다.
$x$ 와 Right Hull의 맨 끝 점 두개를 잇는다.
- $x$ 와 두 점을 이은 공간 안에 있는 점들을 지운다.
- 지워나가다 공간 밖에 있는 점이 나오면 x와 잇는다.
- 공간 안에 있는지 판단은 CCW를 통해 할 수 있다.
  - 만약 x를 넣어가며 CCW를 하다 자신이 처음으로 들어간 CCW와 그 다음 x가 들어온 CCW가 다르다면 공간 안에 들어가는 지점인 것이다. 접선의 개념과도 동일함. 아래서 예시를 보면 더 이해가 잘 됨.
- 이 과정은 다시 말하면 접선을 찾는 과정과 동일하다.
끝날 때 까지 하고 Left Hull과 병합

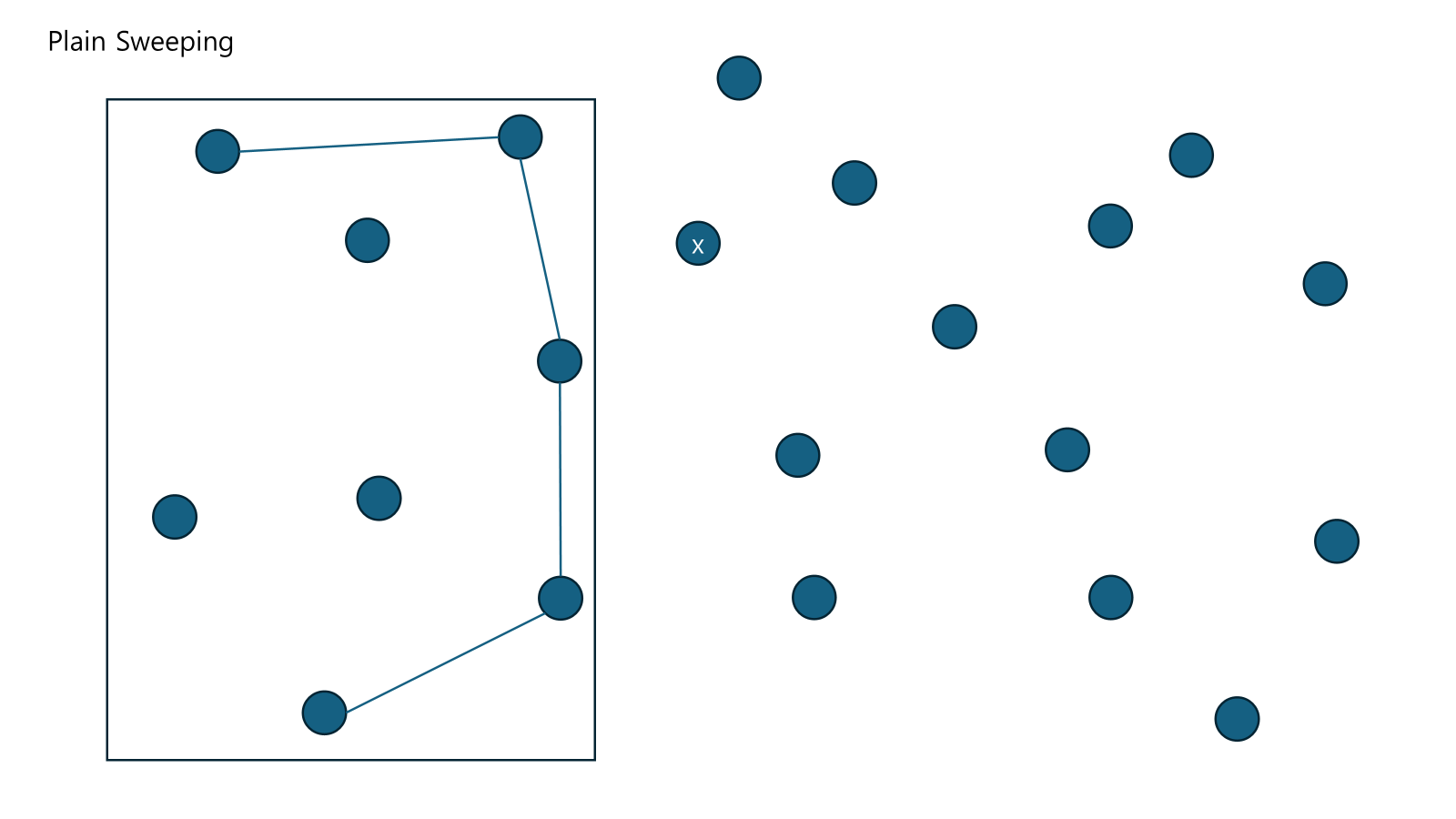
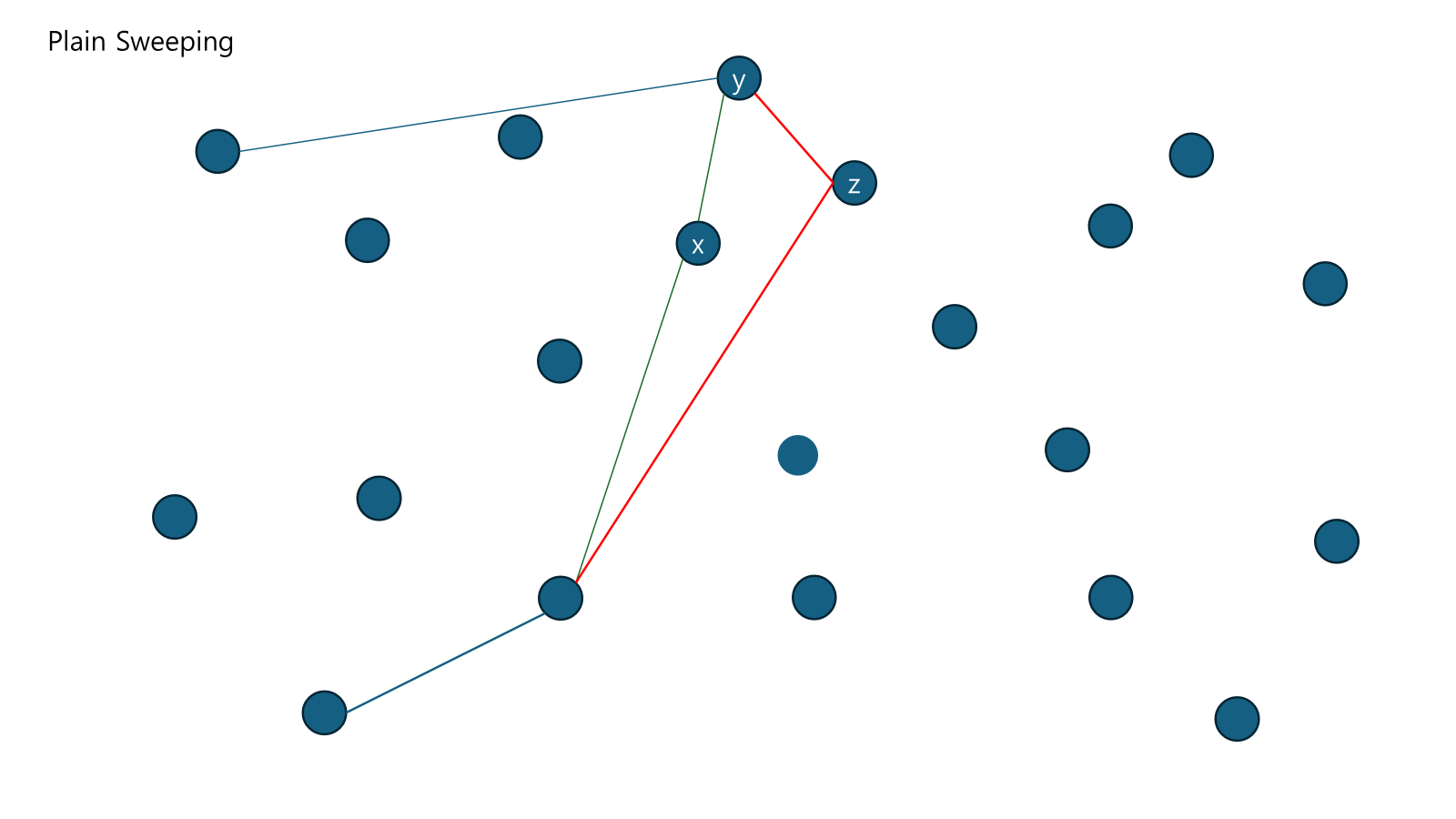
Plain Sweeping이 어느정도 진행되었다. 네모 안에 Right Hull이 있으며 x가 추가되는 상황이다.

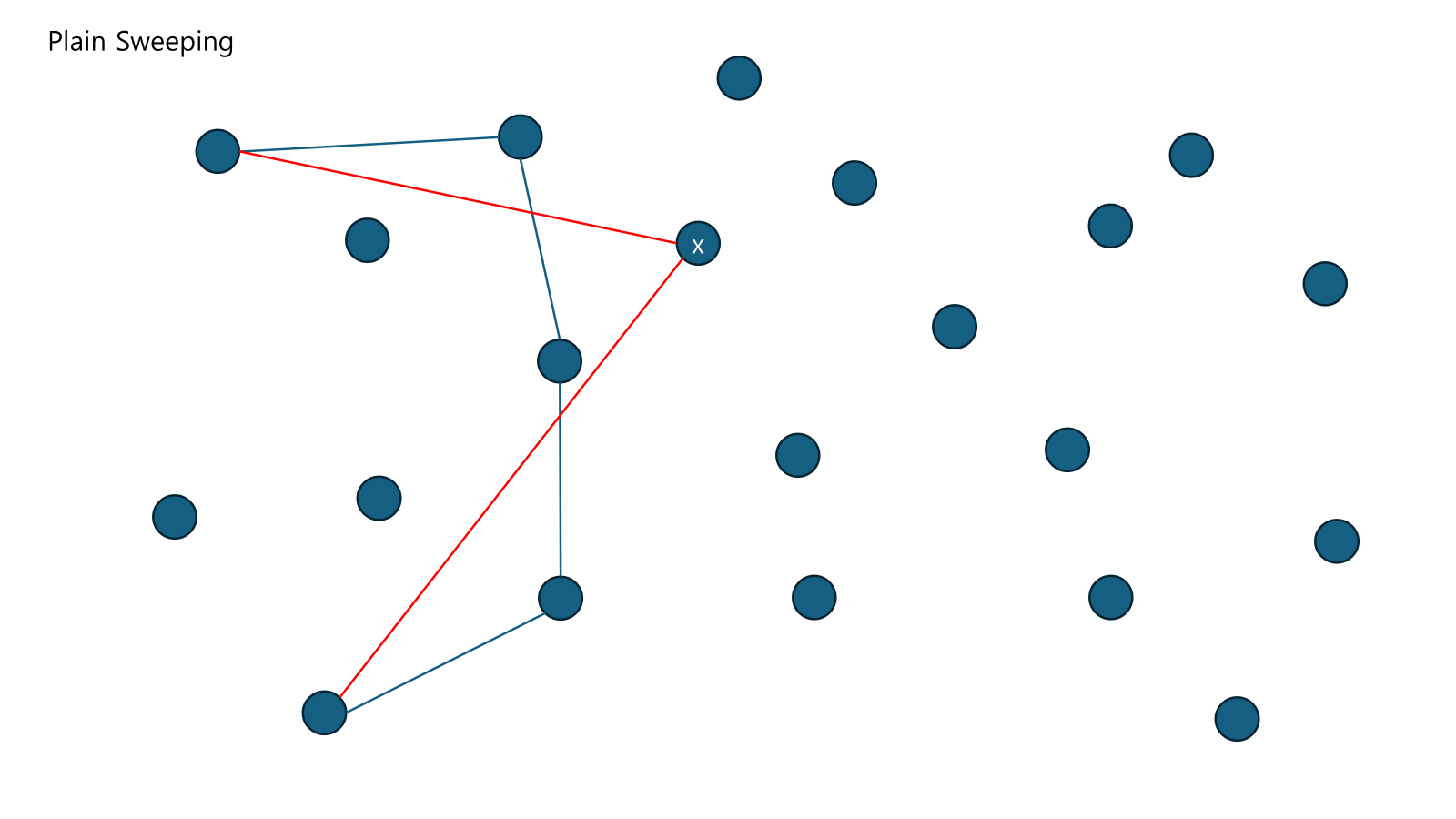
맨 끝점과 x를 잇는다. 공간 안에 있는 점을 지운다.

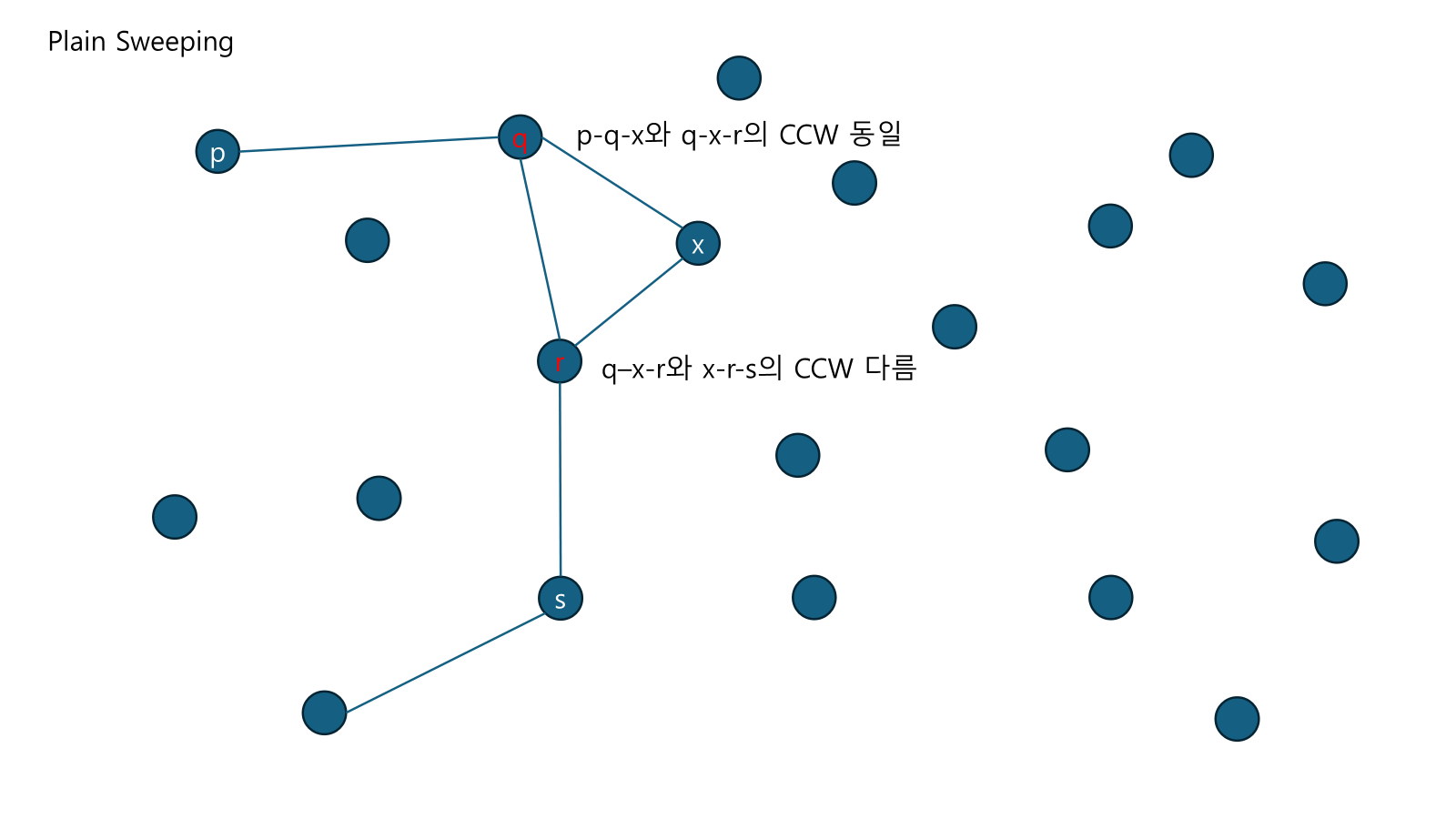
점이 공간 안에 있는지를 파악하게 도와주는 자료다. p-q-x와 q-x-r의 CCW는 동일하나 q-x-r과 x-r-s의 CCW는 다르다. r은 공간 안에 처음 들어오는 점이다. 이를 반대 방향으로 하면 1개나 2개의 점이 나오고 점과 점 사이의 점을 모두 지우면 된다.

이는 접선을 찾는다고 말할 수 있다. 공간 사이에 점이 무수히 많이 있으면 접하는 선을 찾는다고 예기할 수 있기 때문이다.

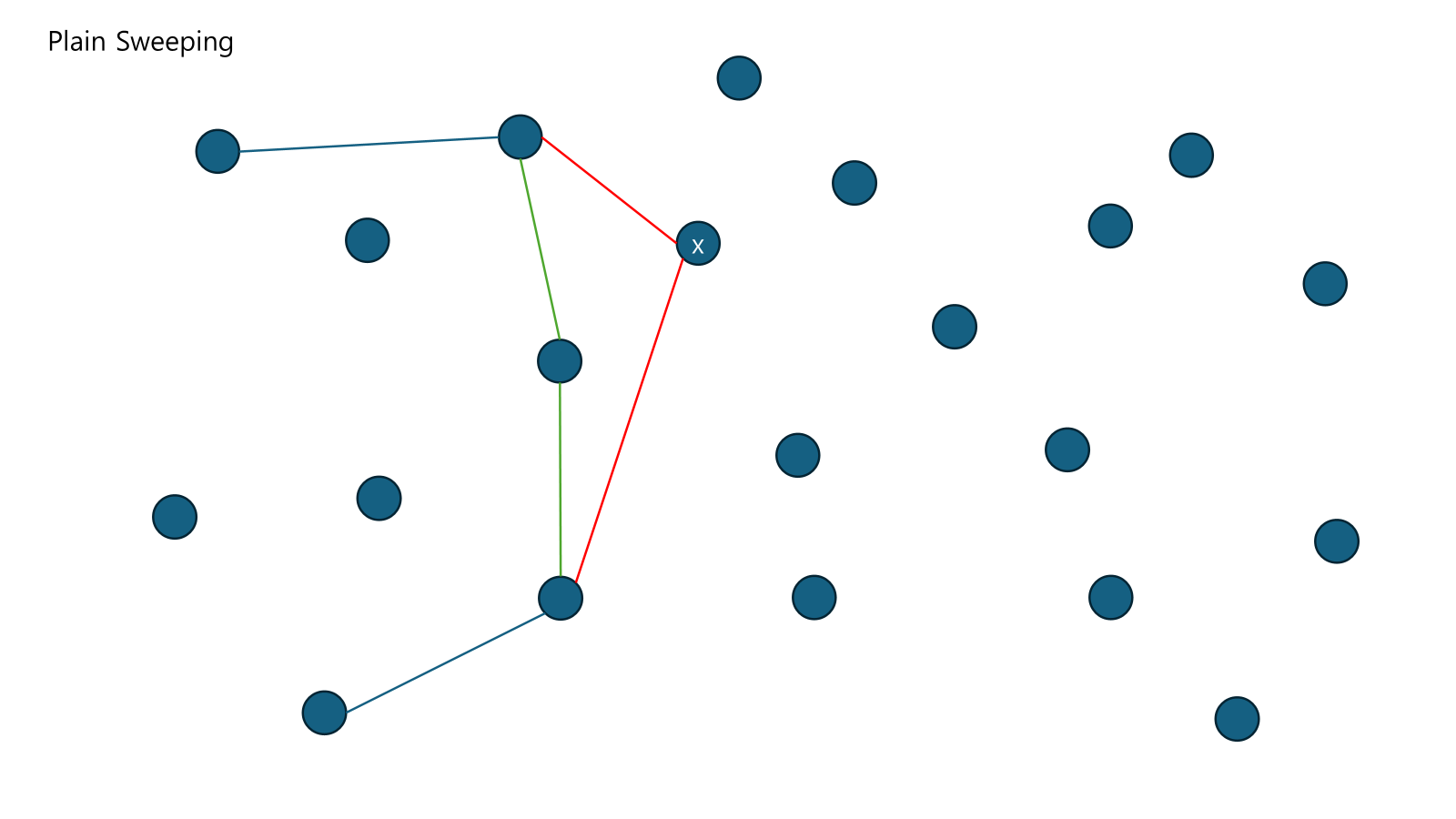
지워 나가다가 공간 밖에 있는 점과 연결한다.

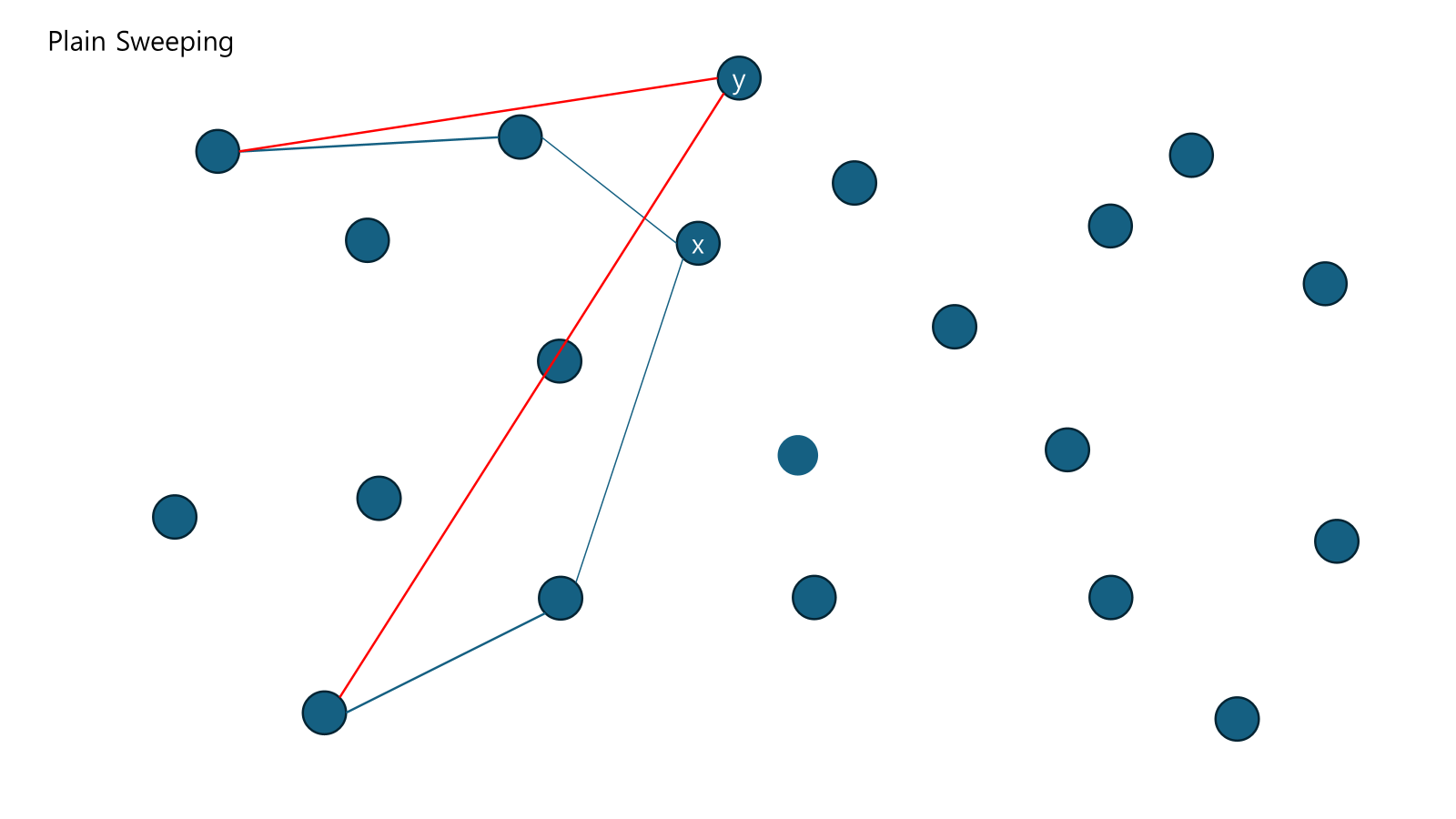
다시 제일 왼쪽에 있는 점 y가 들어온다.

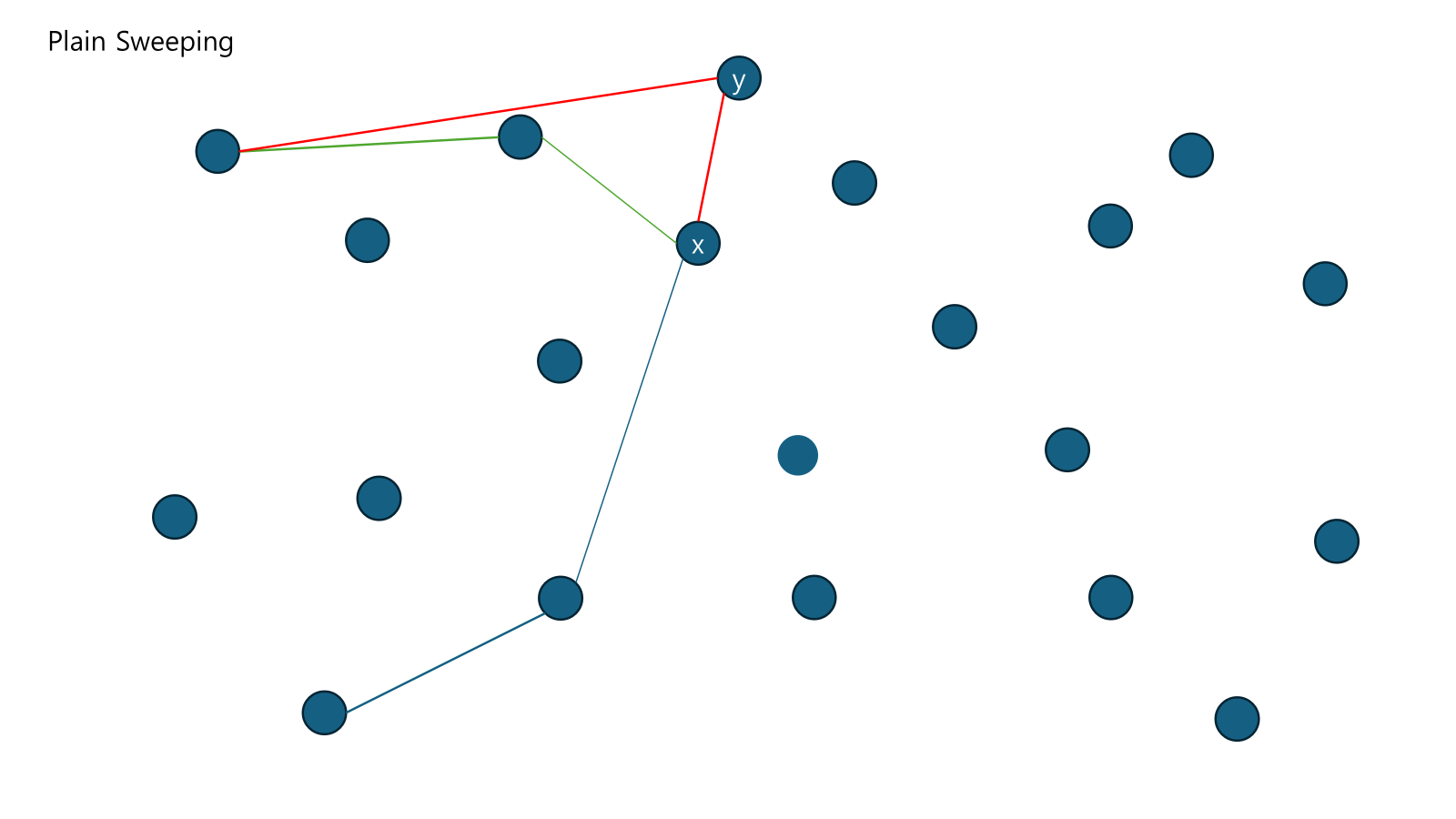
이하 반복

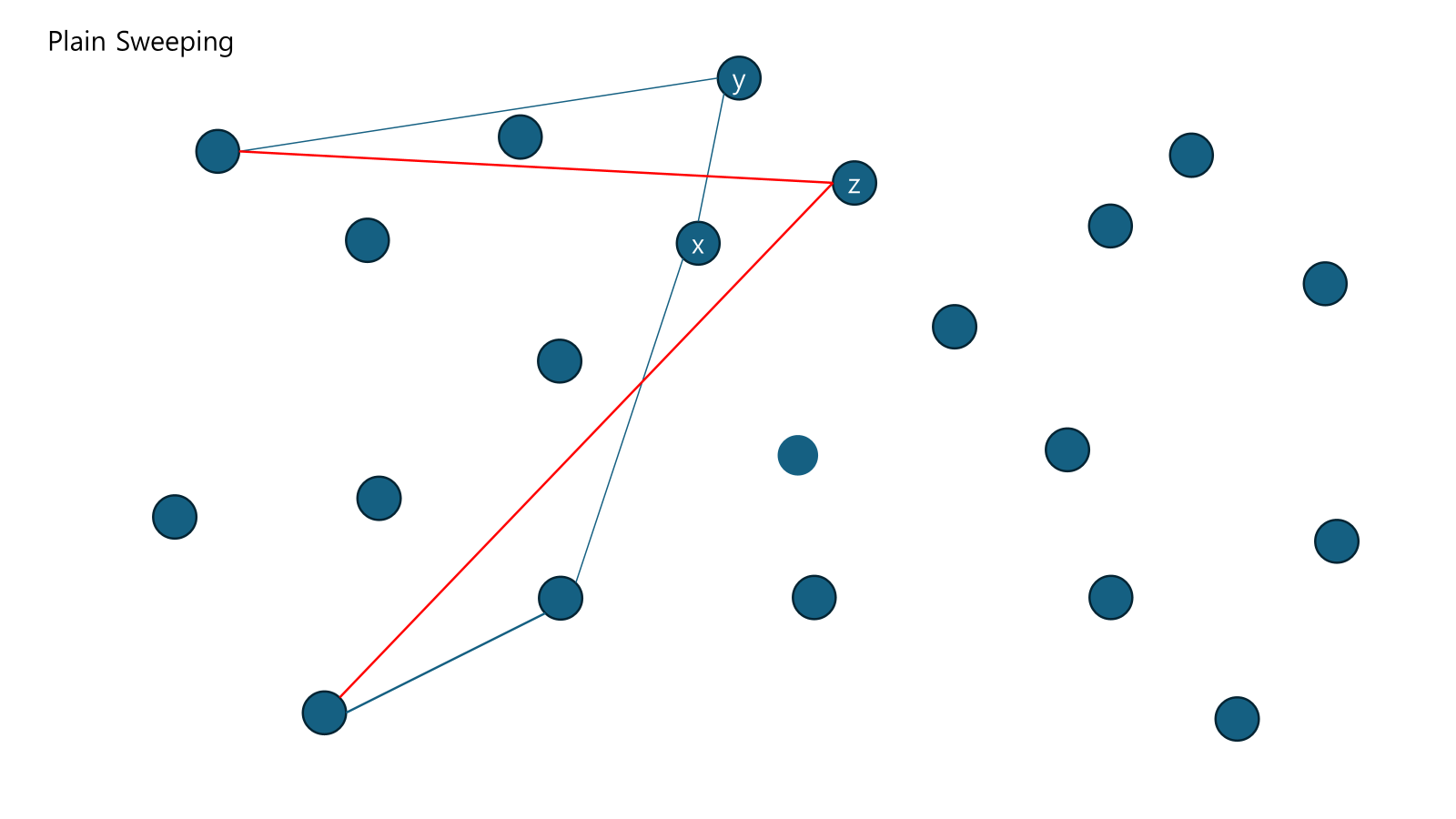
점을 찾는 과정은 어찌 보면 $O(n)$ 으로 보여 시간복잡도가 $O(n^2)$ 이라고 생각할 수 있다. 하지만 Balanced Tree로 구현하면 이진 탐색하듯이 찾을 수 있다. 그러므로
$O(nlogn)$ 의 시간이 걸린다.

Dynamic Case

$O(nlogn)$ 을 통해서 Convex Hull을 만들었을 때, 새 점이 추가되면 어떻게 해야하는가?

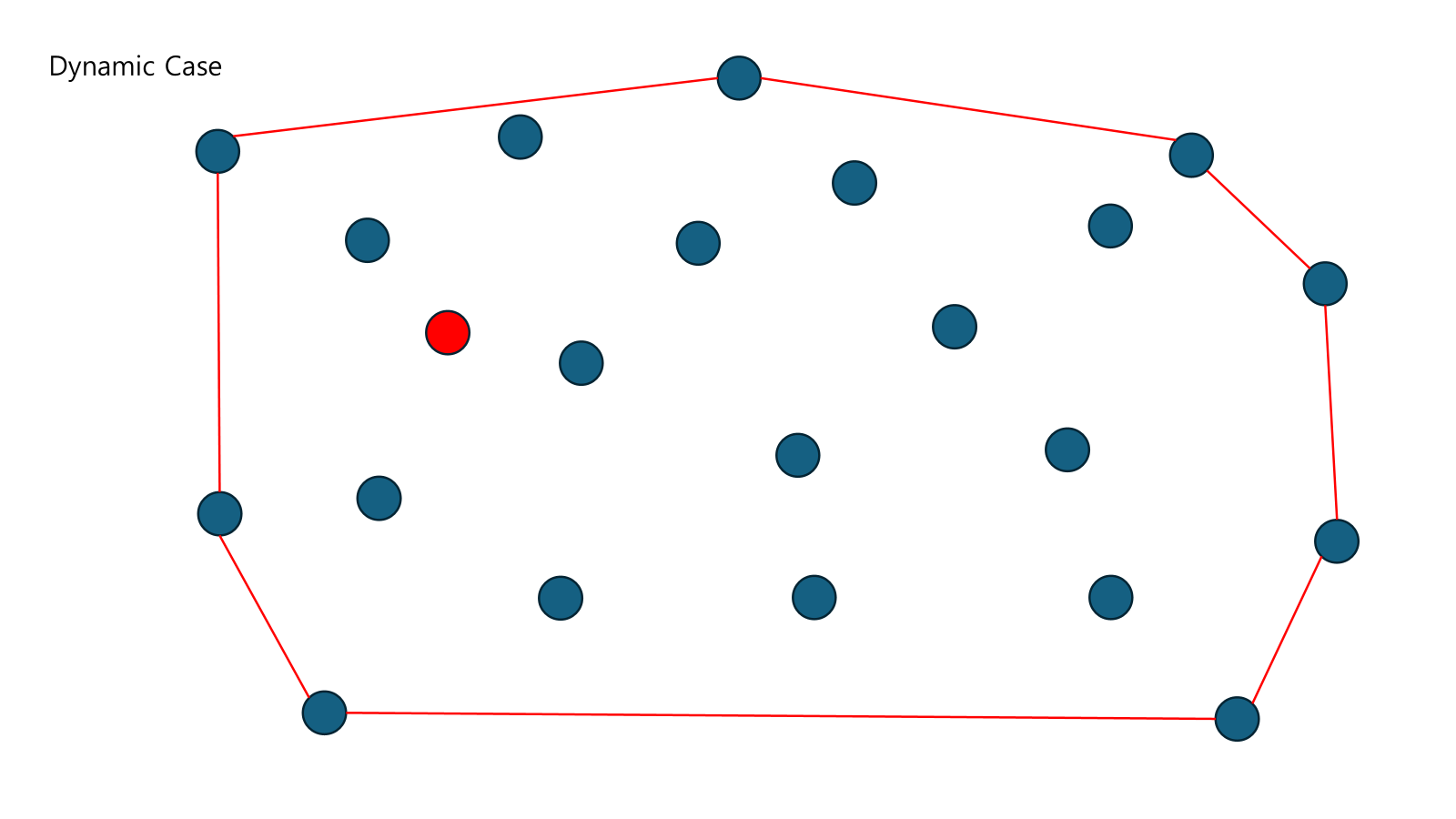
먼저, 안에 새 점이 추가되면 특별히 수행할 일은 없다. 점의 안과 밖의 구분은 앞에서 말한 방법과 Balanced Tree를 이용한다.

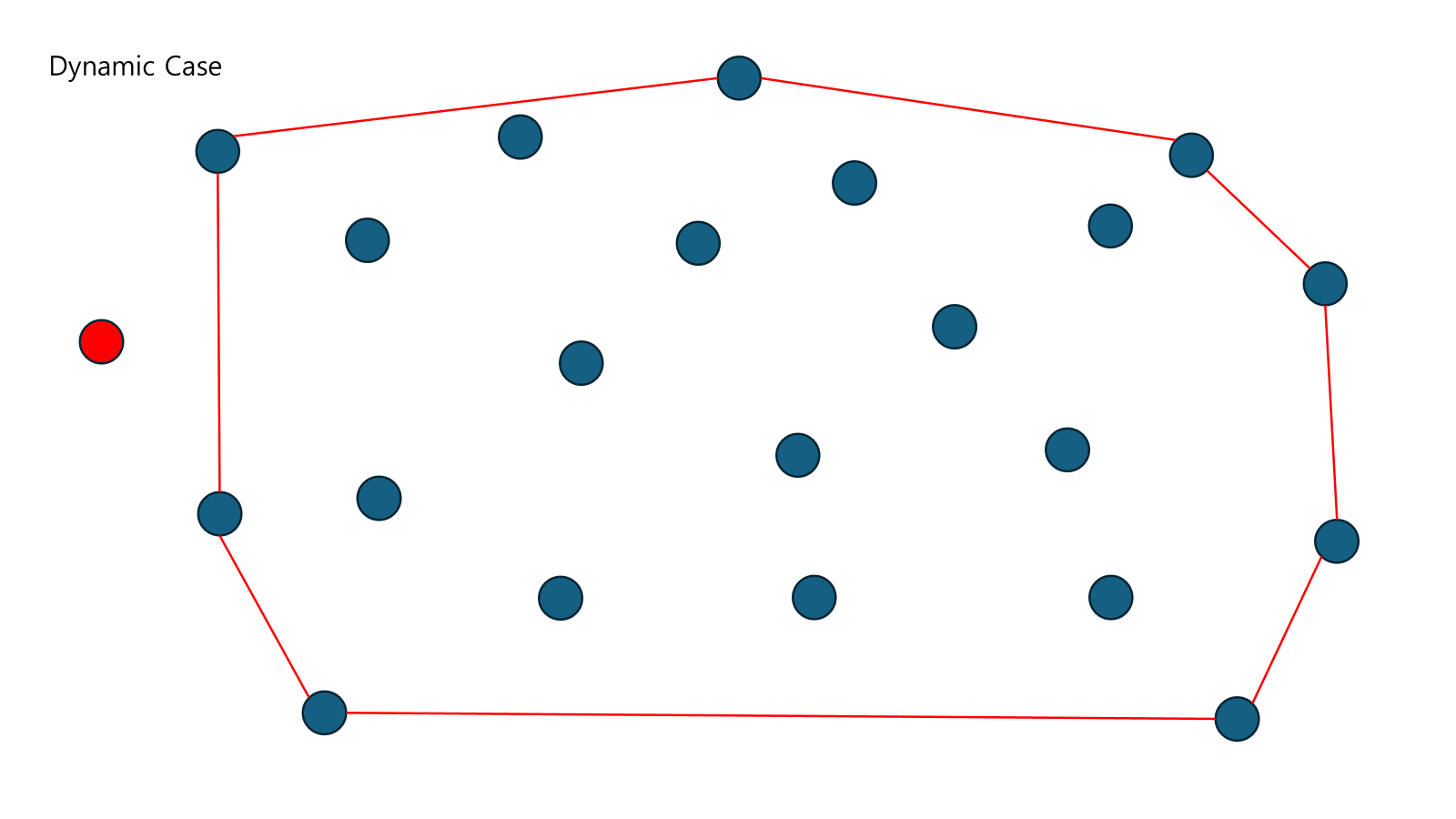
밖에 새 점이 추가되면 접선을 그어 해결한다.

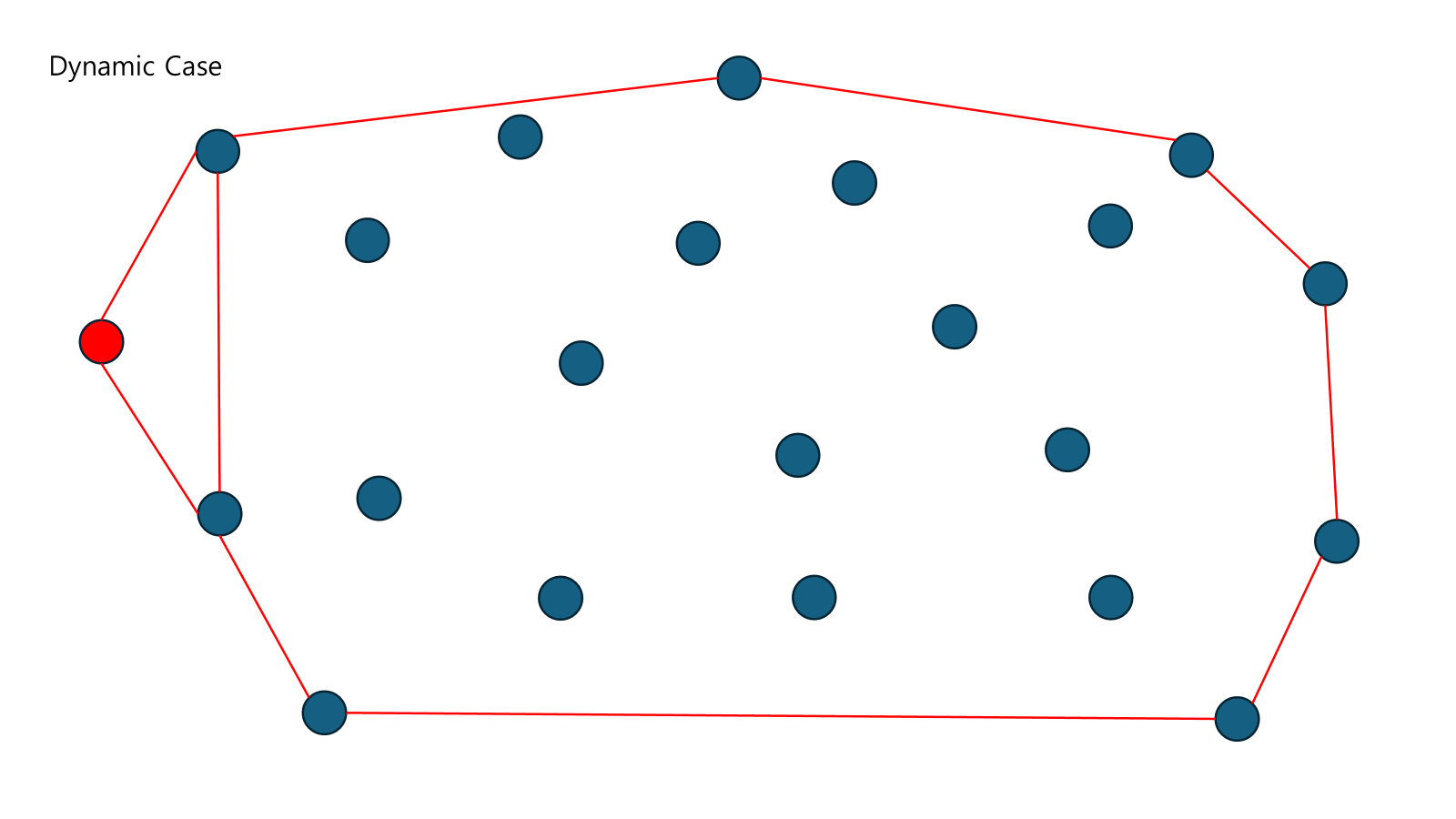
Divide and Conquer

$O(nlog^2n)$

Upper Hull Only
반으로 나눠서 왼쪽 Upper Hull과 오른쪽 Upper Hull 을 구한다.
두개를 merge한다.
- 공통 접선을 찾는다.
- 왼쪽에서 아무 점이나 설정한다.
- 오른쪽도 아무 점이나 설정한다.
  - 먼저 왼쪽에서 앞으로 진행하며 접선이 되는지 확인한다.
  - 그 후 오른쪽에서 앞으로 진행하며 접선이 되는지 확인한다.
  - 공통 접선이 될때까지 반복한다.

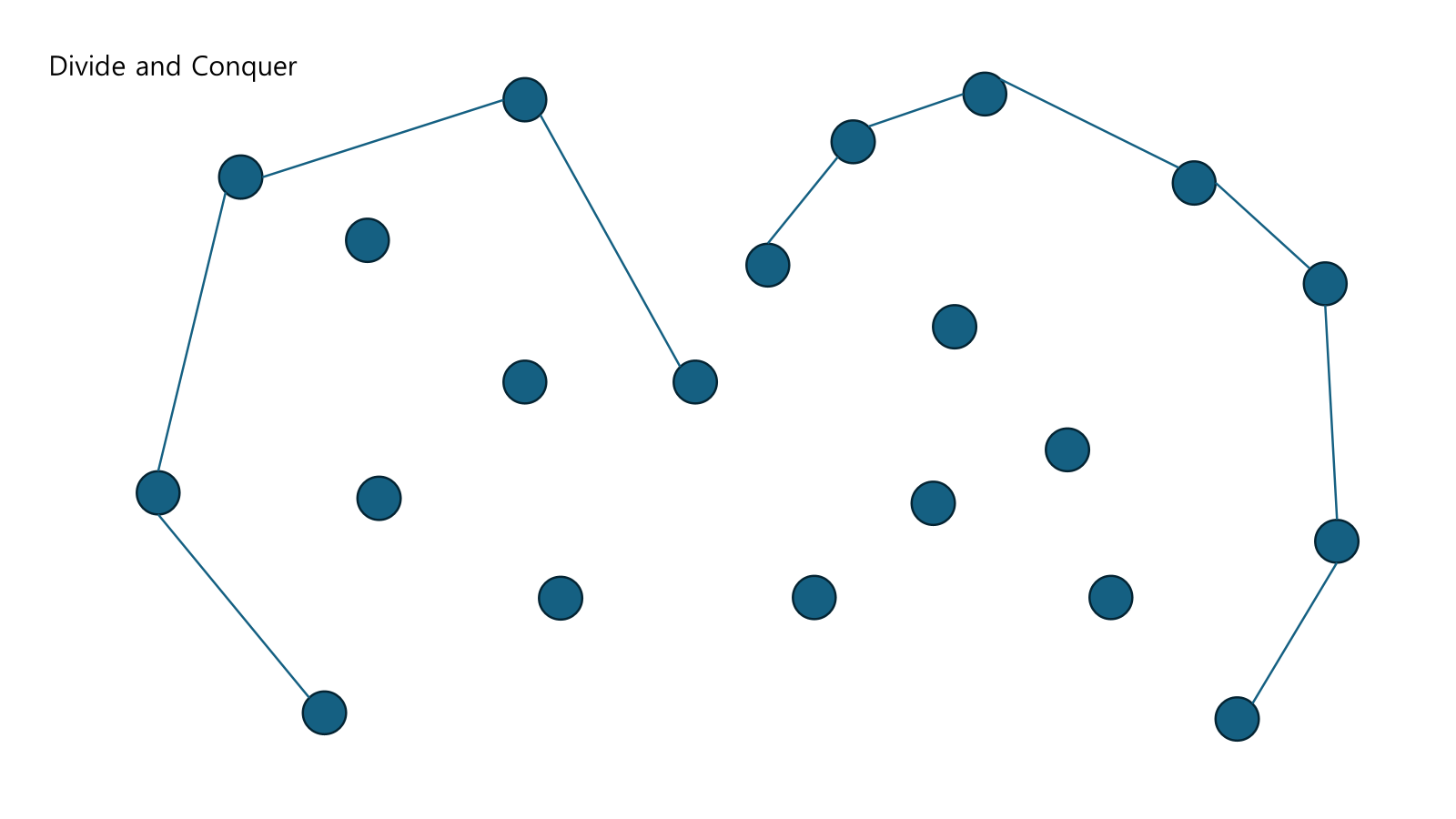
Left Upper Hull과 Right Upper Hull이 있다.

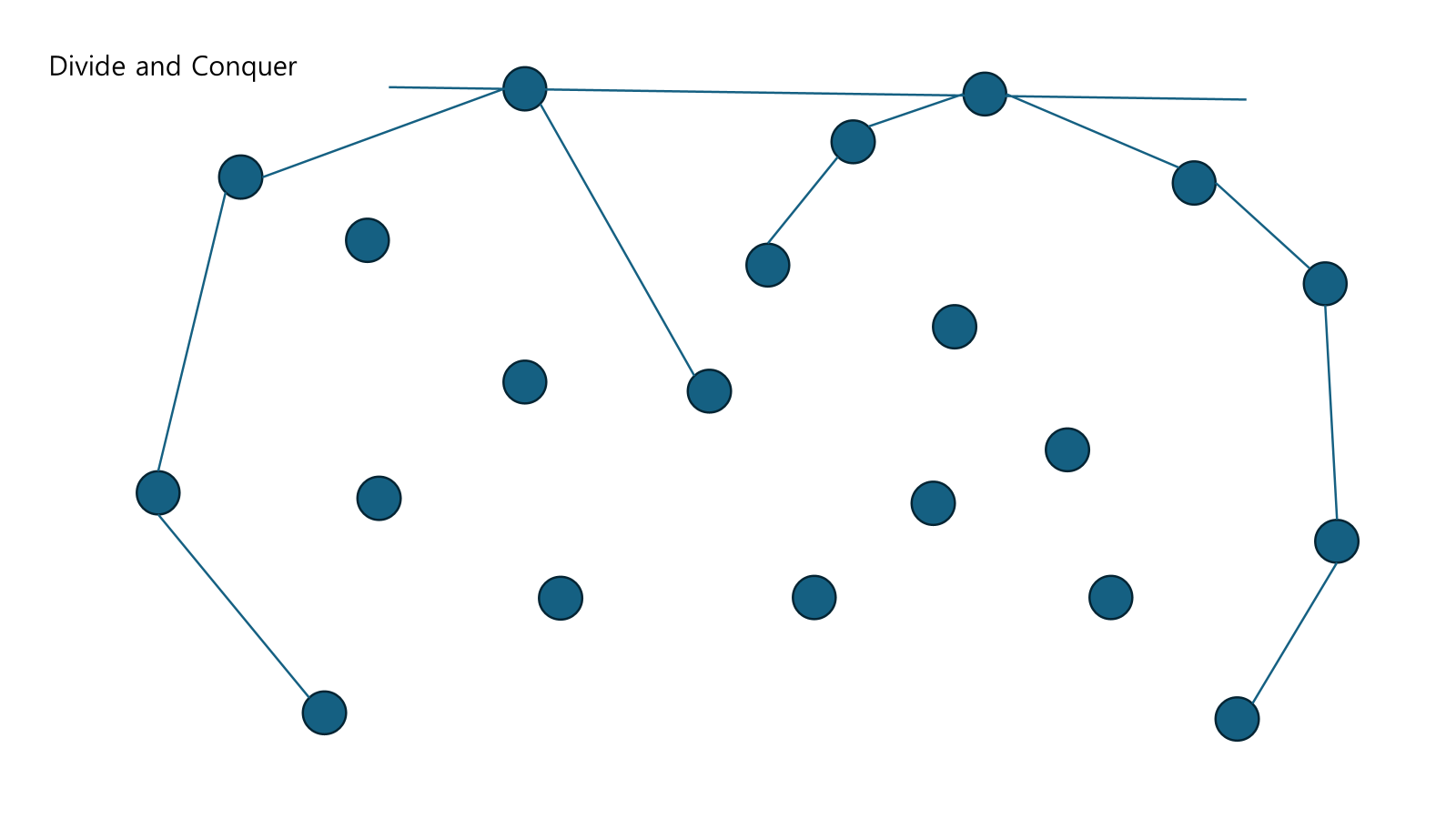
우리는 공통 접선을 찾아서 두개를 이어줘야 한다.

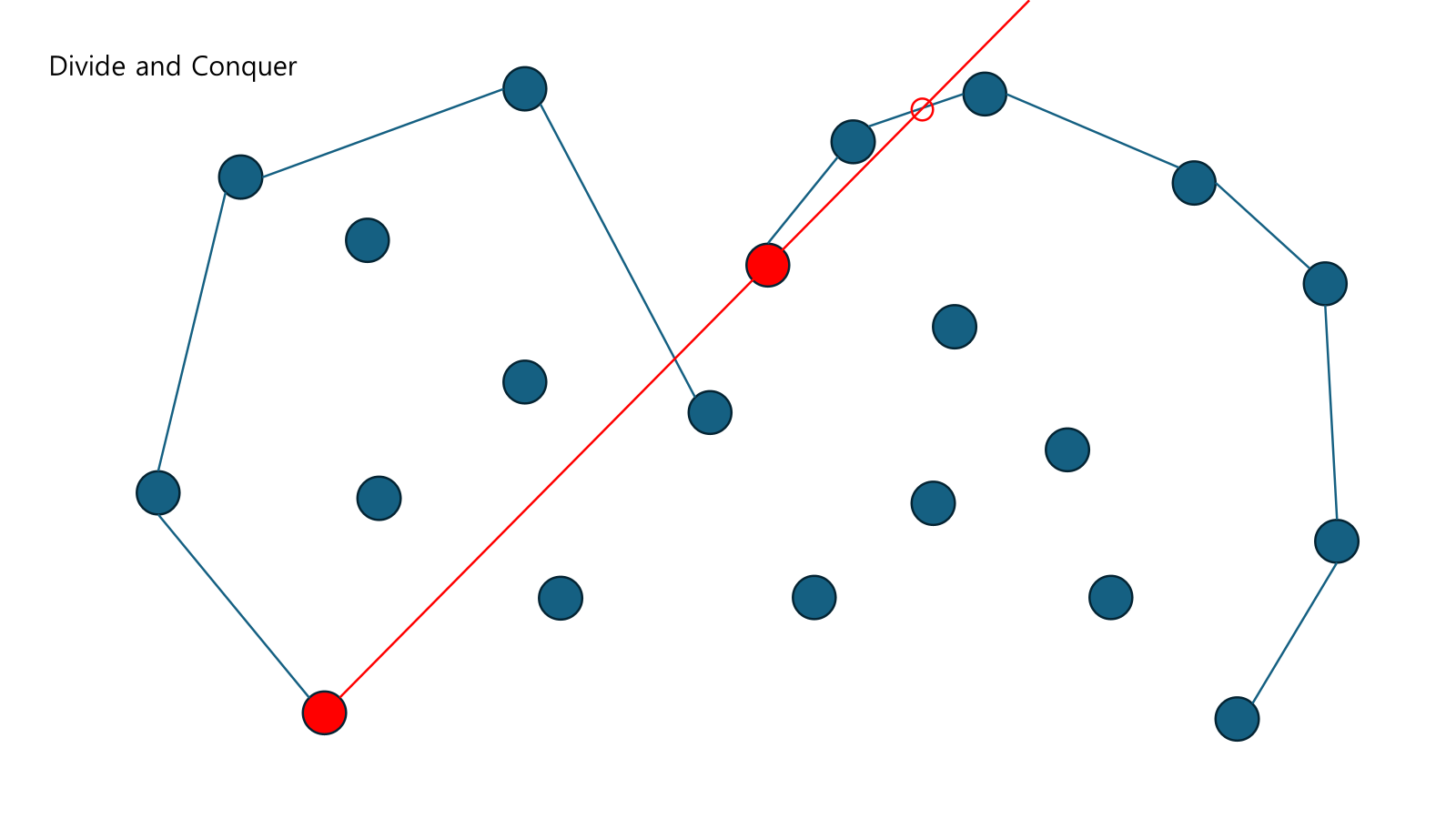
각 Upper Hull의 제일 왼쪽부터 시작해서 뚫고 지나가는 지 확인을 한다. CCW를 통해 가능하다. Right Upper Hull쪽에서 뚫고 지나간다.

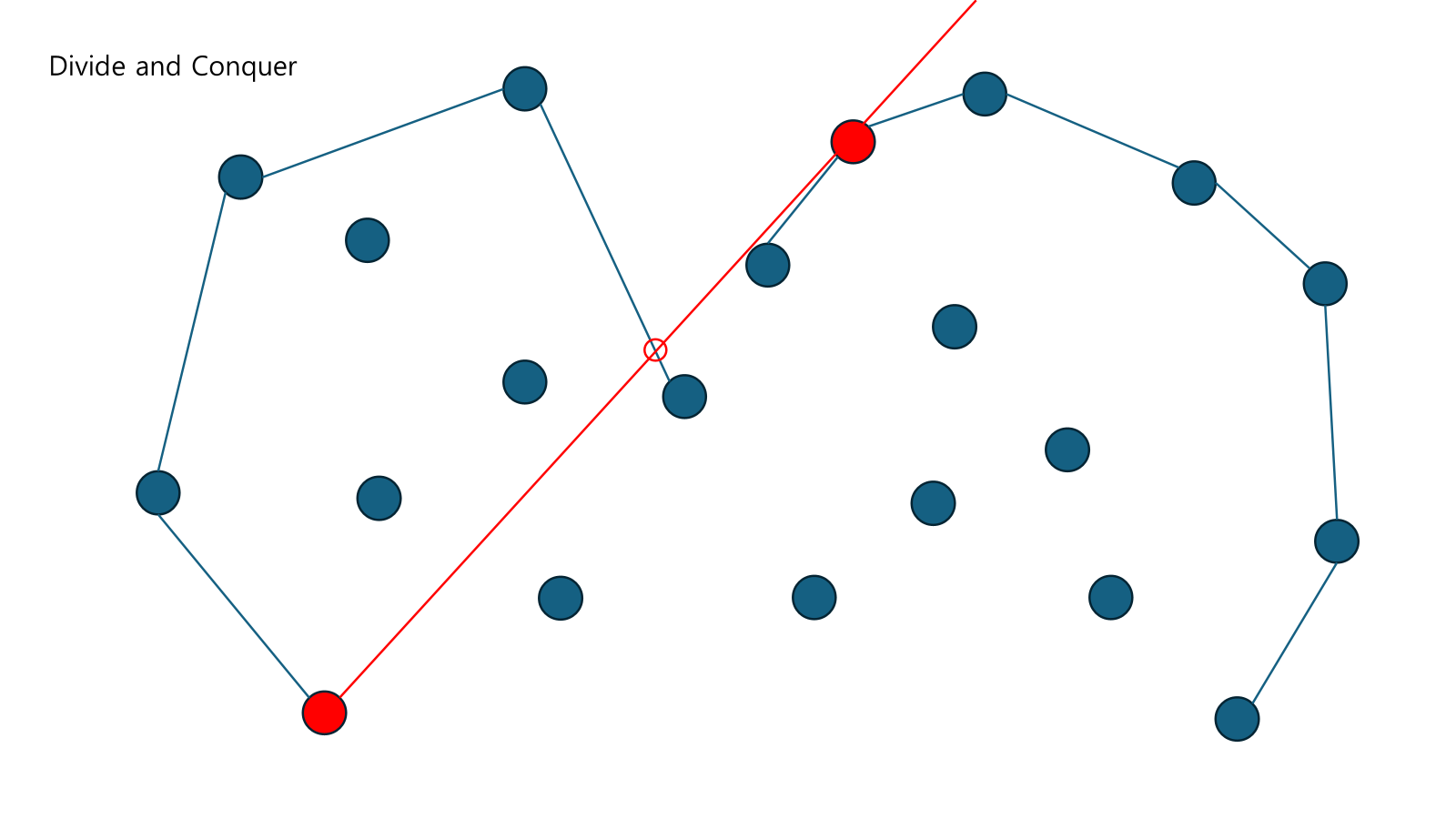
Right Upper Hull쪽에서 뚫고 지나갔으므로 오른쪽의 설정점을 한 칸 옮겼다. 이번엔 Left Upper Hull쪽에서 뚫고 지나간다.

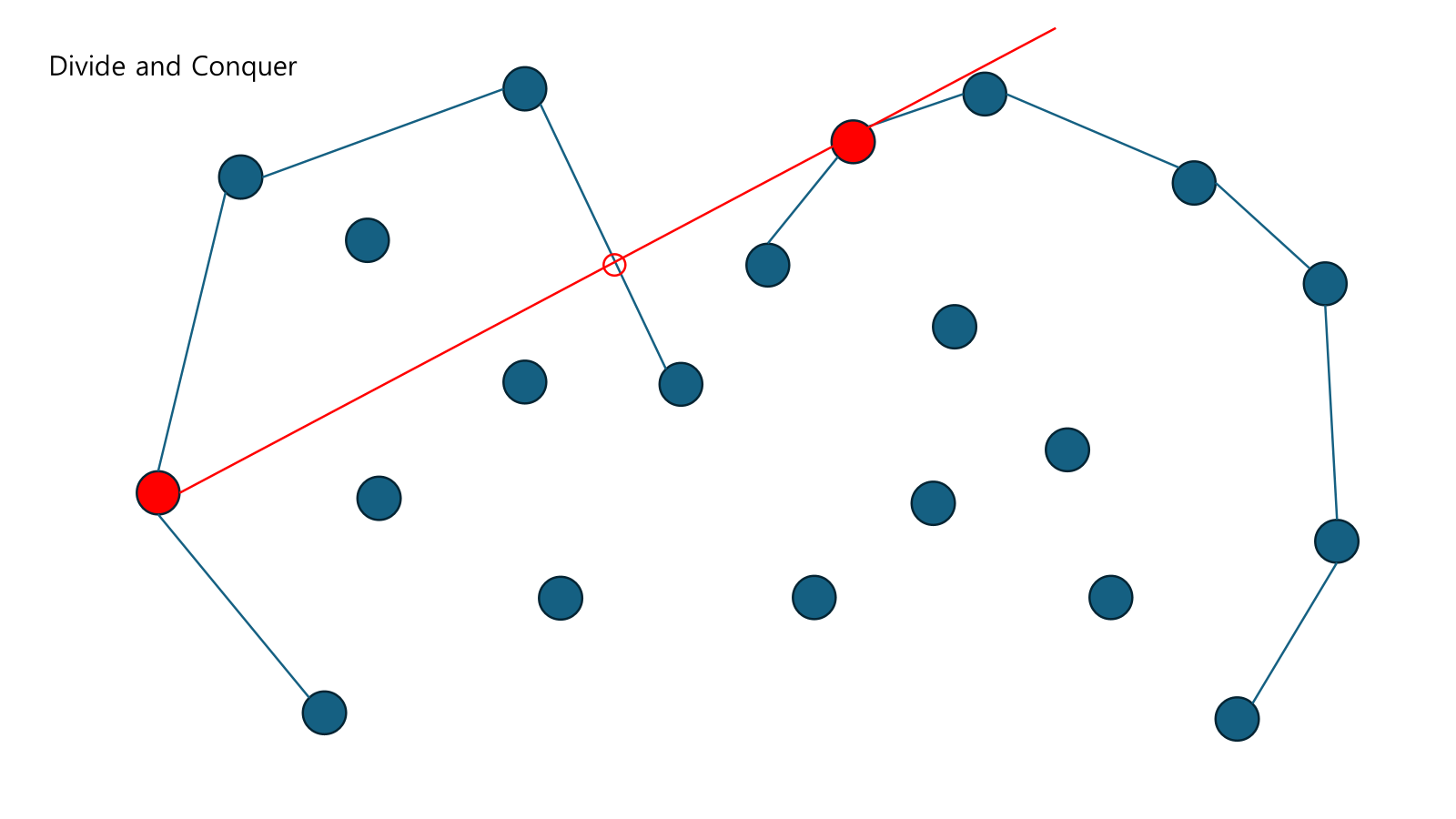
Left Upper Hull쪽에서 뚫고 지나갔으므로 왼쪽의 설정점을 한 칸 옮겼다.

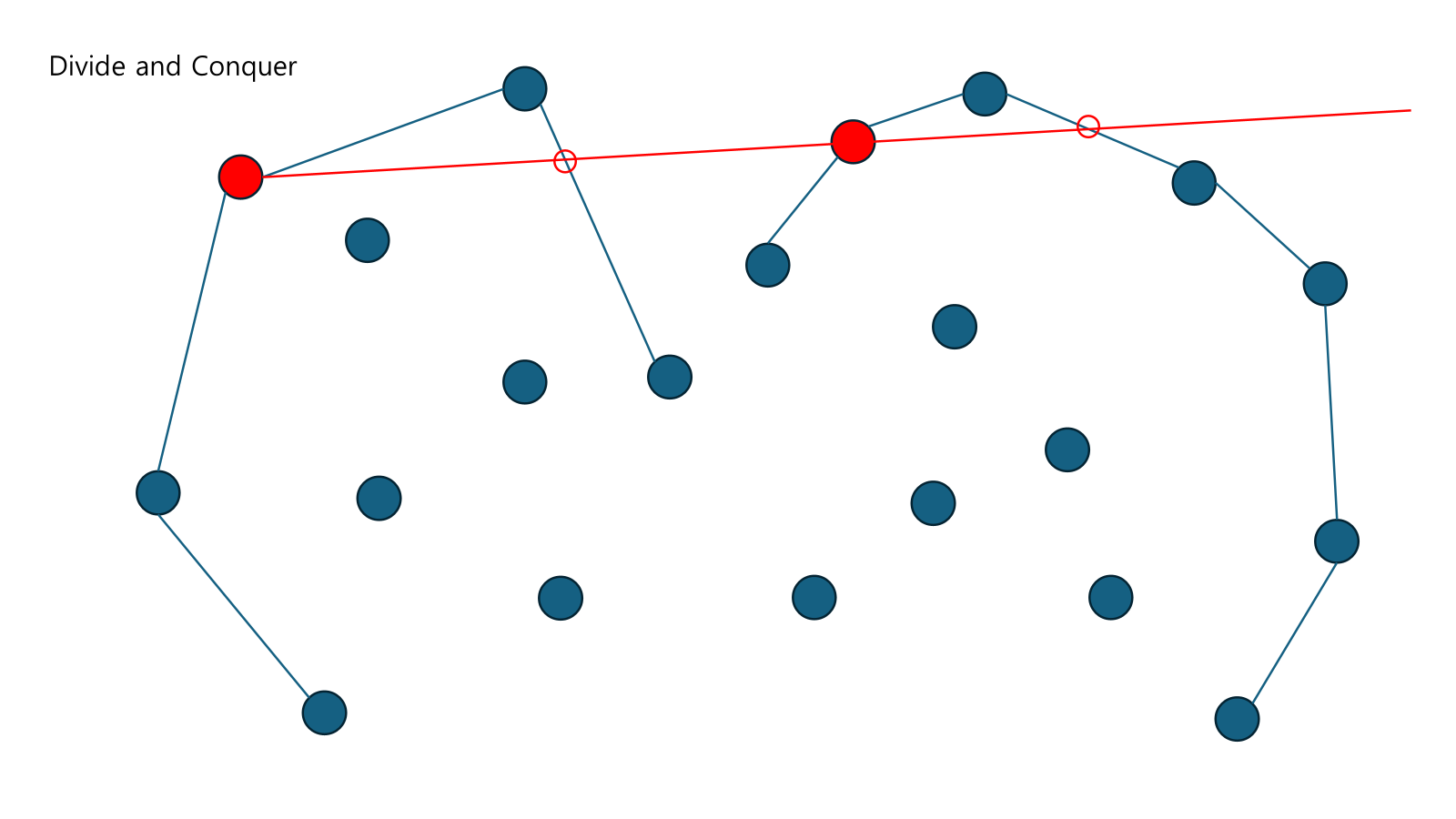
두개가 중복되면 아무거나 옮겨도 상관없다.

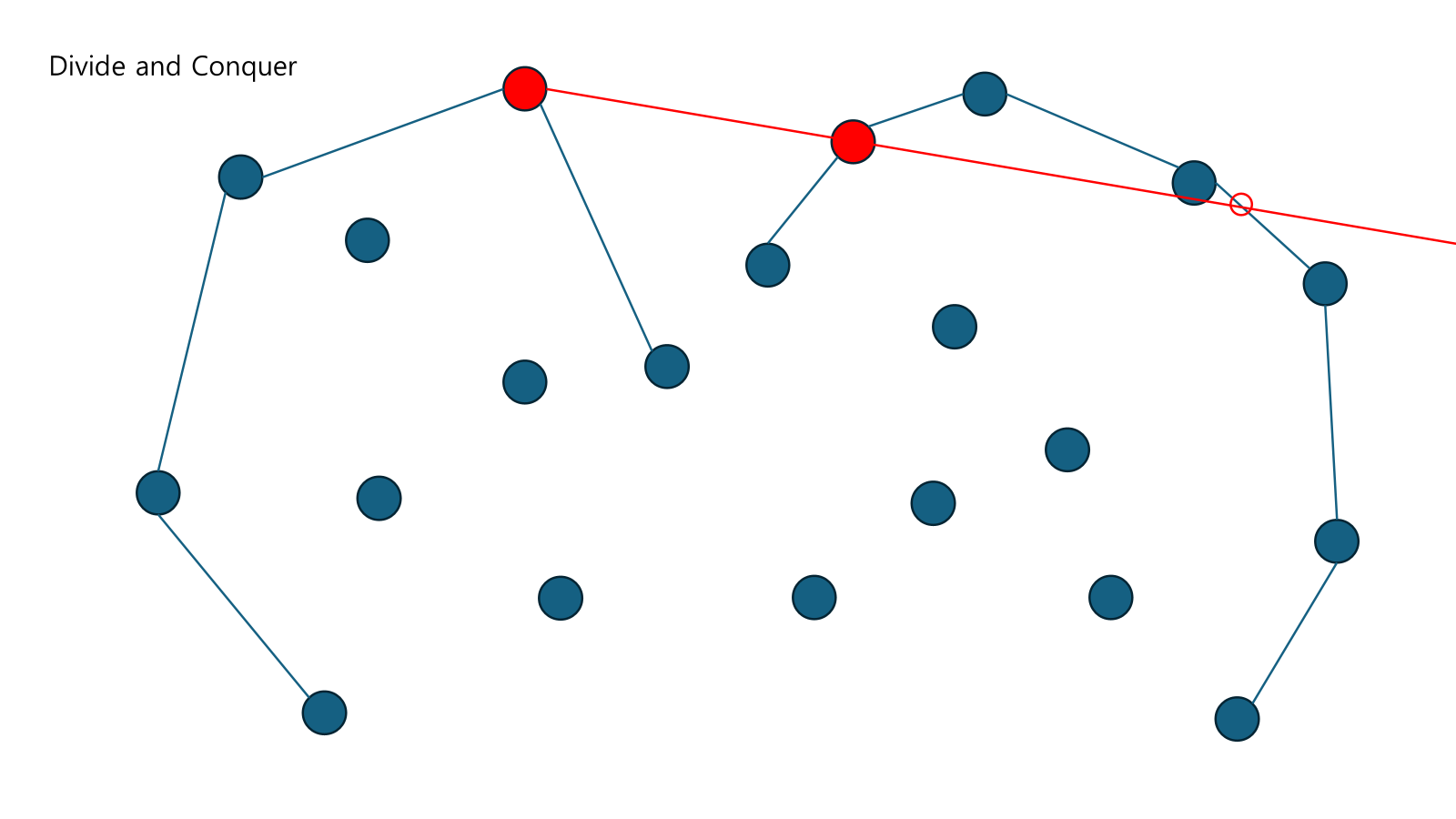
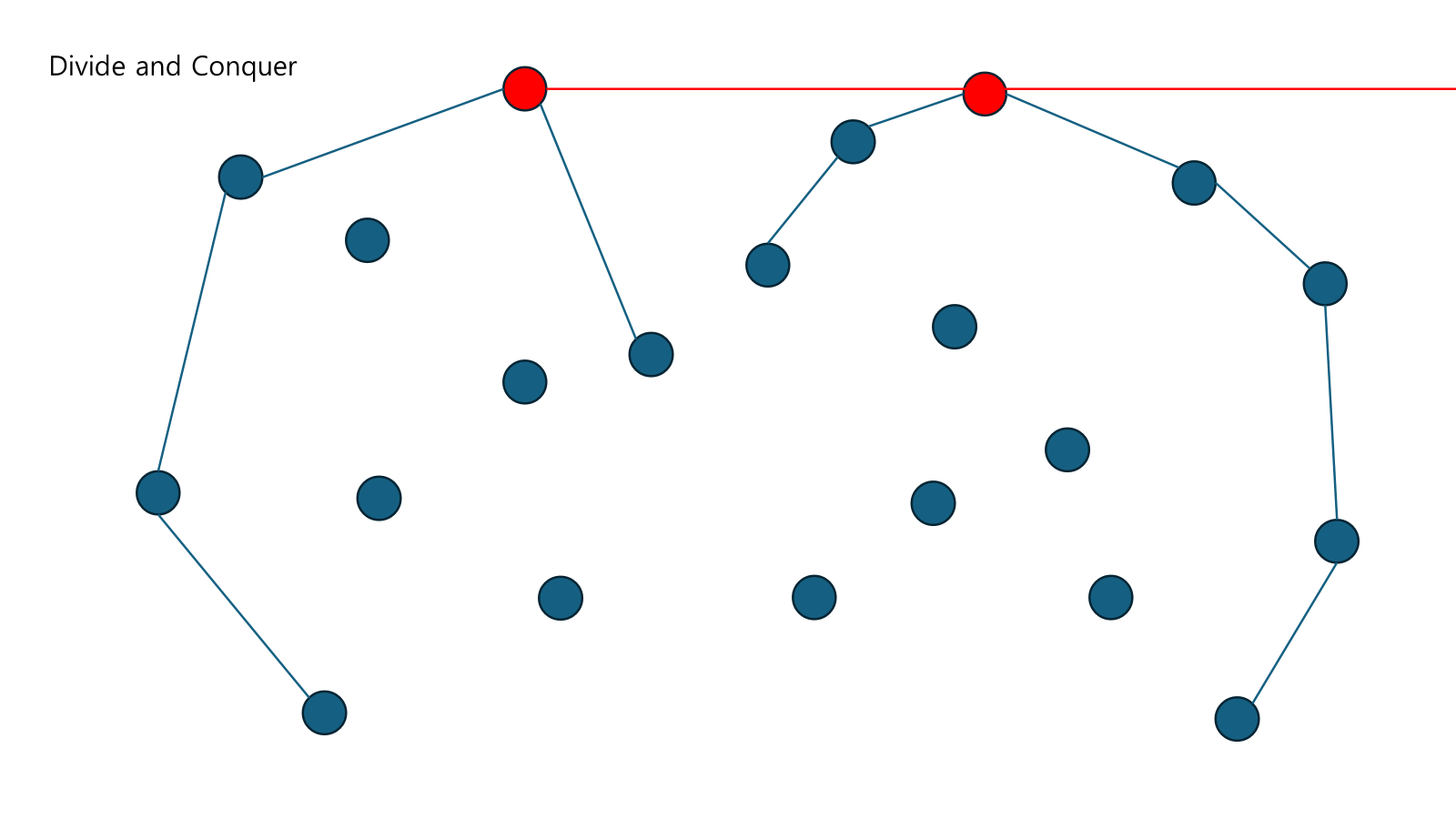
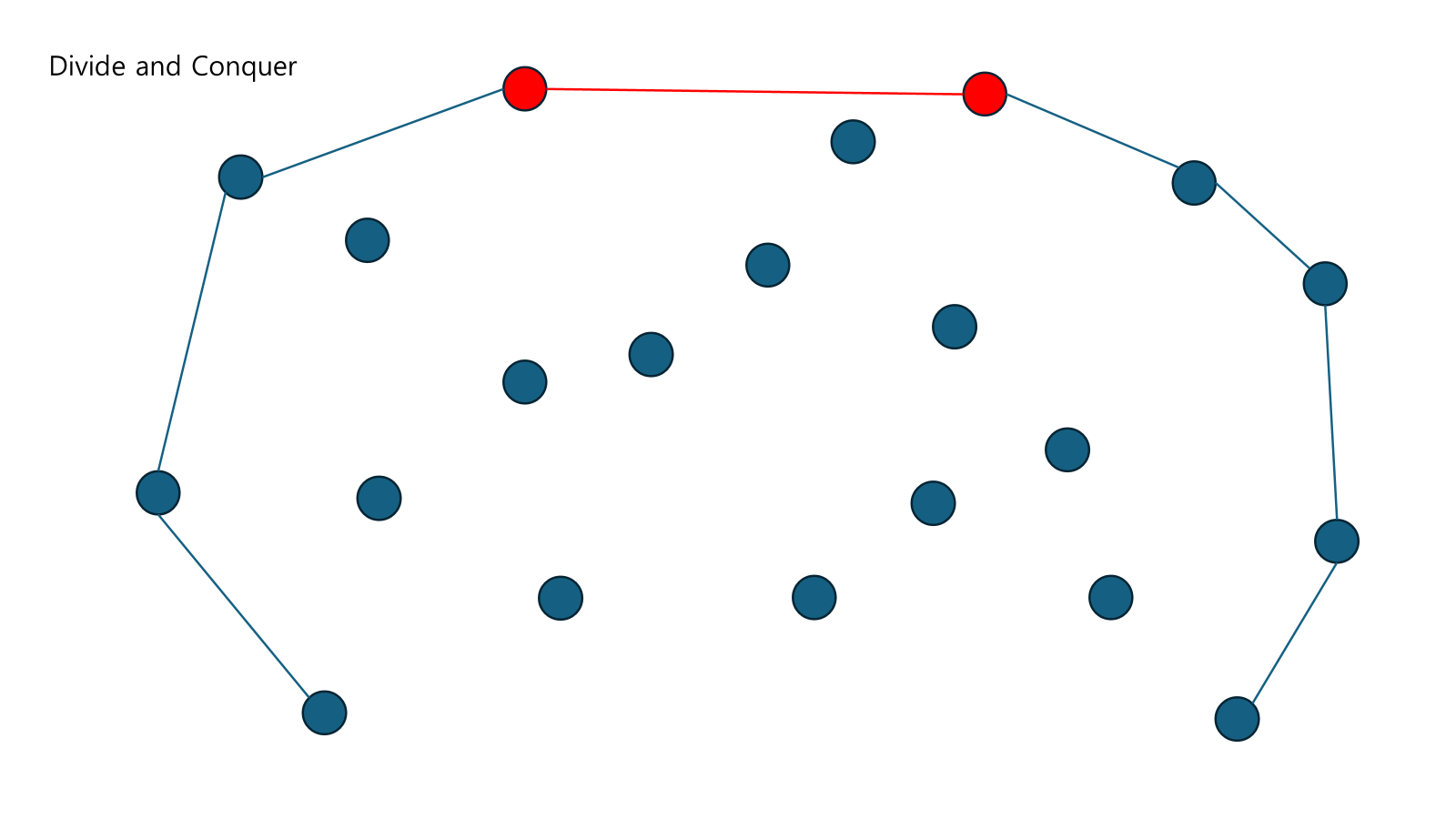
두 점을 이어주고 Balanced Tree를 통해 안에 있는 점들을 없애준다.

Fartest Point

제일 먼 점 2개에 대해서 옆에 테두리를 그리고 테두리를 돌리면서 찾는 방법이다.
정렬하는 시간이 $O(nlogn)$ 이 걸리는 것을 제외하면 점은 $n$ 개를 찾으므로 알고리즘 자체는 $O(n)$ 의 시간이 걸린다. 다만 총 계산은 정렬하는 시간을 포함하므로 $O(nlogn)$ 이 걸린다.

한 방향으로 테두리를 돌린다.

두 테두리 중 하나라도 서로 두 점을 만나게 되면 잇는다.

테두리를 갱신하고 다시 반복한다. 이번엔 아래서 만났으므로 두 점을 잇는다.

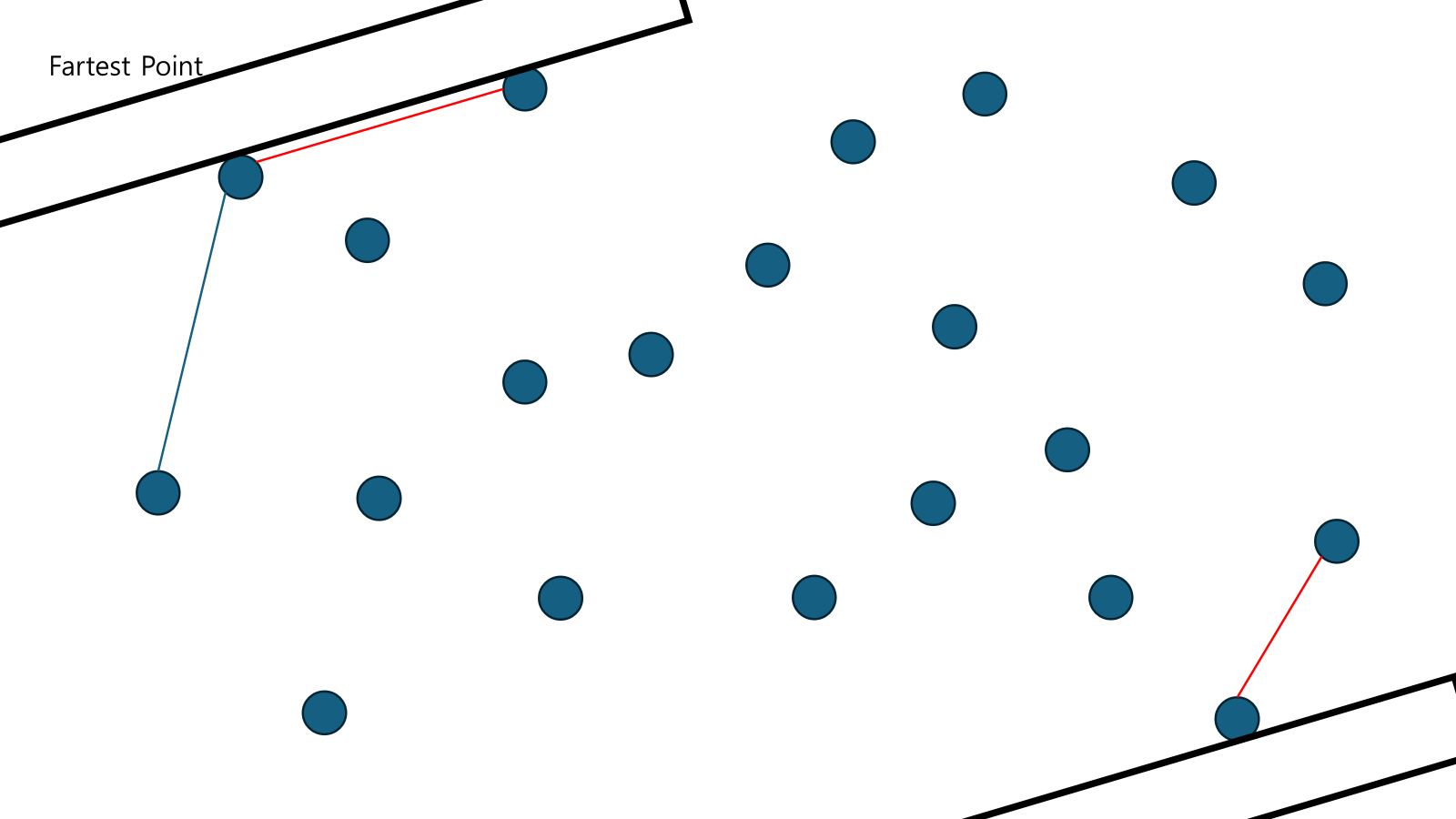
다시 위에서 만났다. 또 이어준다.

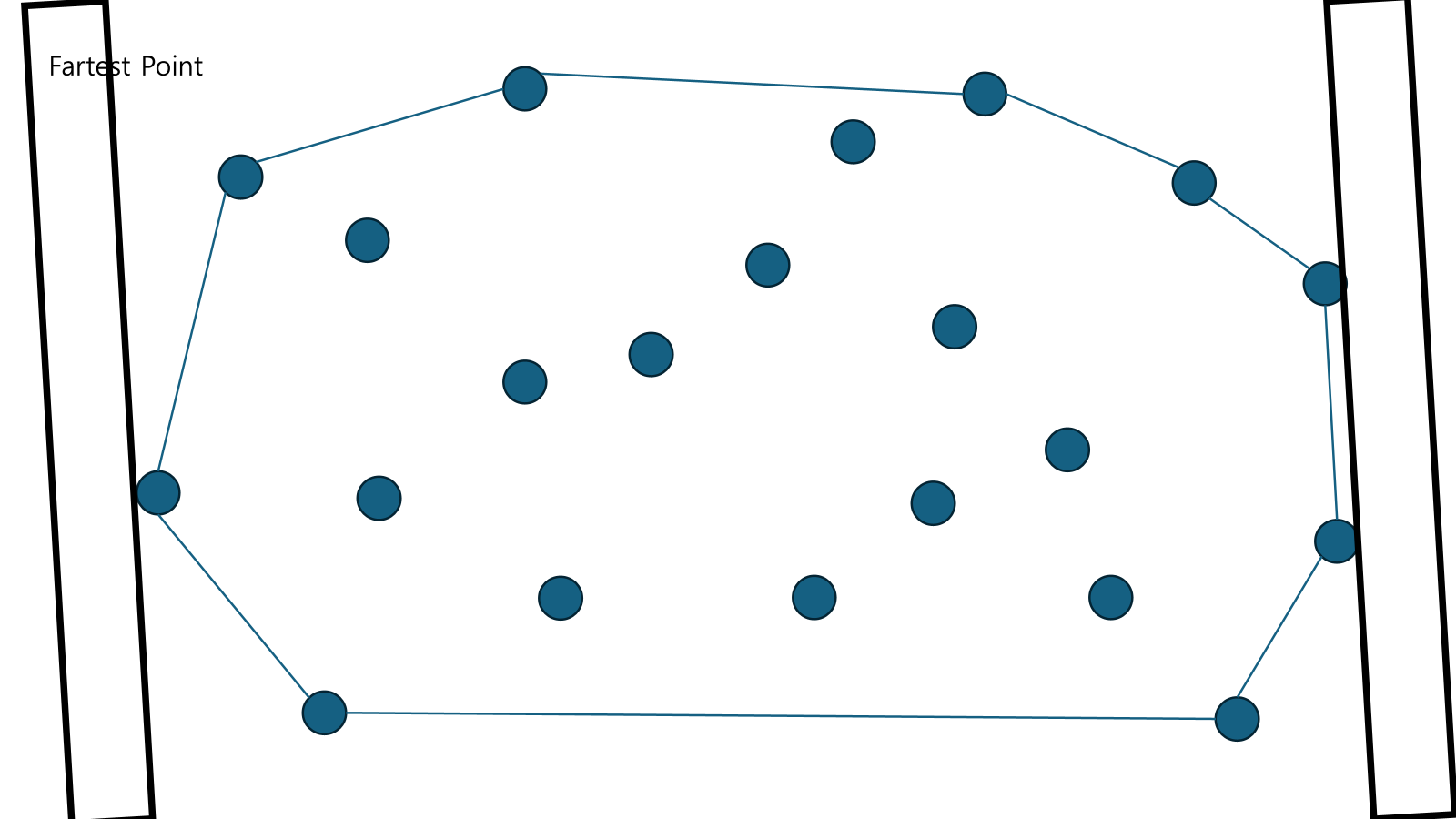
Convex Hull이 만들어지면 종료한다.