Context-Free Grammars

Context-Free Languages

어떤 language는 finite automata와 reuglar expression으로 나타낼 수 있다는 것을 알았다. 하지만 어떤 language는 나타낼 수 없다는 것도 알았다. 예시로 {$0^n1^n | n ≥ 0$}같은 것들이 있다.

regular language가 아닌 것들에 대한 설명이다. 잘 모르겠으면 여기를 참고하자.

이제 더 많은 일을 할 수 있는 모델과 language를 배워보자.

---

Context-Free Grammars

다음과 같은 context-free grammer $G_{1}$이 있다.

• $A → 0A1$
• $A → B$
• $B → \#$

Context-Free Grammer는 3가지로 구성된다. Symbol, Arrow, String이다.
Symbol을 왼쪽, String을 오른쪽에 두며, 둘 사이를 Arrow로 이어준다. 이 의미는 왼쪽에 있는 Symbol을 오른쪽의 String으로 바꿀 수 있다는 뜻이다.
이 때 왼쪽의 Symbol을 variable이라고 부르며, 이 variable들과 다른 symbol들로 구성된 오른쪽의 String을 terminal이라고 부른다.
Context-Free Grammer는 start variable을 가지고 있다. 특정하게 지정하지 않는 한 맨 처음에 있는 variable이 start variable이다.

예시를 통해 더욱 자세히 보자.

위에 있는 $G_{1}$은 $A,B$의 variable들을 가지고 있으며, $A$는 start variable이다. $0,1,\#$이라는 terminal들을 가지고 있다. Grammer $G_1$을 통해서 여러가지 string을 만들어낼 수 있다. 만드는 방법은 다음과 같다.

1. start variable을 쓴다. 특별하게 표시되어 있지 않는 한 제일 위의 왼쪽 variable이 start variable이다.
2. 이 variable로 시작하는 규칙을 찾는다. variable을 규칙에 따라서 오른쪽의 terminal로 바꾼다.
3. variable이 남지 않을 때 까지 반복한다.

중요한 건 variable이 남으면 안된다는 것이다. 0과 1의 개수가 동일한 string을 만들 때, $000A111$이면 variable이 남았으므로 문법을 따라 계속 진행해야 한다. 모두 없어져야만 string이 만들어진 것이다.

하나의 예시로, 위에 있는 $G_{1}$은 000#111을 만들어낸다. 이 때 만들어내는 과정을 derivation이라고 할 것이다. derivation은 특정한 string을 만들어내는 substitution의 나열이다.

$G_{1}$에서 000#111의 derivation은 $A ⇒ 0A1 ⇒ 00A11 ⇒ 000A111 ⇒ 000B111 ⇒ 000\#111$

이러한 dervation을 표현할 때 parse tree를 사용하곤 한다. 문법에 따라 완성되는 string이 어떤 과정을 따라가는 지 보기 편하기 때문에 많이 사용한다.

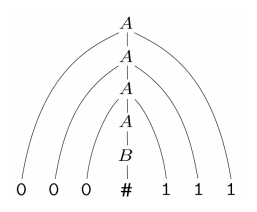
편리함을 위해서, variable이 같은 rule을 단순화 할 수 있다. $G_1$은 $A → 0A1$와
$A → B$가 있다. 이 둘을 한줄로 합쳐서 $A → 0A1 | B$로 나타낼 수 있다. "|"나 "or"를 사용한다,

Context-Free Language

이렇게 문법을 통해 만들어낼 수 있는 string들을 모은 것이 Context-Free Language이다.

$L(G_1)$는 $G_1$에 대한 language of the grammar다.

$L(G1)$은 {$0^n\#1^n | n ≥ 0$}로 나타낼 수 있다.

Context-Free grammar로 만들어낸 language를 Context-free language(CFL)라고 한다.

---

Formal Definition of a Context-Free Grammars

context-free grammar는 4-tuple $(V, Σ, R, S)$로 나타낸다.
1. $V$는 variable의 유한 집합이다.
2. $Σ$는 terminals의 유한 집합이며, $V$와 disjoint하다. 다시 말해 $V$와 $Σ$에 겹치는 부분은 없다.
3. $R$은 rules의 유한 집합이며, 각각의 rule은 variable과 string으로 구성되어 있다. string은 variables와 terminals로 구성되어있다.
4. $S ∈ V$는 start variable를 의미한다.

$u,v,w$는 variables와 terminals로 구성된 string이라고 하자. $A->w$는 $uAv$가 $uwv$를 yields한다고 하며, $uAv ⇒ uwv$로 쓰인다. 이는 A의 앞과 뒤는 바뀌지 않으며 A를 w로 바꿀 수 있다는 의미이다.
$u,v$에 대해서 derive한다는 개념이 있다. 기호로는 $u \overset{*}{⇒} v$로 쓴다.
이 말의 의미는 다음 두 케이스와 같다.

• $u = v$여서 $u$를 $v$로 바꿀 수 있음.
• $u_{1}, u_{2}, ... , u_{k} / k ≥ 0$이고, $u_{1} ⇒ u_{2} ⇒ ... ⇒ u_{k} ⇒ v$여서 결국 $u$를 $v$로 바꿀 수 있음.
  Context-Free Grammer의 language는 $\{w ∈ Σ^{∗}| S \overset{*}{⇒} w\}$로 표현할 수 있다.

앞에서 본 $G_{1}$을 context-free grammar로 표현해보자.

• $V = {A,B}$
• $Σ = {0, 1, \#}$
• $R$은 위에서 말한 규칙
• $S = A$

context-free language에 대비되는 개념으로 context-sensitive language가 있다. 앞은 그냥 바꿀 수 있지만, 뒤는 앞뒤를 고려하여 바꾼다.

---

Designing Context-free Grammars

• Creative한 일임
• 첫번째로, 많은 CFL는 간단한 CFL들의 합이다.
  • 다시 말하면, CFL는 작은 CFL의 Union이므로, 한번에 설명하기 어려우면 작은 것들부터 구현하여 전체를 완성할 수 있다.
• 두번째로, language에 대해서 DFA를 먼저 그릴 수 있으면 CFG는 만들기 쉬워진다.
  • DFA의 각각의 상태 $q_{i}$에 대해서 $R_{i}$를 만든다.
  • DFA의 $δ(q_{i}, a) = q_{j}$에 대해서 $R_{i} → aR_{j}$를 만든다.
  • DFA의 accept state에 대해서 $R_{i} → ε$를 만든다.
  • DFA의 start state $q_{0}$를 $R(R_{0})$로 만든다.
• 세번째로, context-free language는 two substring으로 이루어져 있으며, 그 둘은 "linked"되어 있다. 무한할 수도 있는 정보를 기억해야하며 정보들이 나머지 부분과 대응하는지 검증해야 한다.
  • $R -> uRv$
  • 이 방법을 통해서 앞에 있는 $u$에 $v$가 대응하는지를 확인한다.
  • 예시로 $\{0^n1^n | n ≥ 0\}$이 있을 때, $0S1$을 통해 앞의 '0'에 뒤의 '1'이 늘어나는 방향으로 대응할 수 있다.
• 네번째로, 어려운 구조의 language는 string이 나올 때마다 재귀적으로 지금의 구조가 나올 수 있다. 그러면 재귀적으로 만들면 된다.

---

Ambiguity

grammar는 다른 방법으로 같은 string을 만들 수 있다.
이는 programmaing langauge 같은 곳에서는 별로 좋지 않다. 프로그램은 주어진 문법에 대해서 동일한 결과를 내놓아야 하지만 모호함으로 인해 결과가 달라지면 문제가 생기기 때문이다.

예시를 보자. grammer $G_5$의 Formal Definition이다.

$(V, Σ, R, S)$
1. $V = \{EXPR\}$
2. $Σ = \{+,X,(,),a\}$
3. $R = \{⟨EXPR⟩ → ⟨EXPR⟩+⟨EXPR⟩ | ⟨EXPR⟩X⟨EXPR⟩ | (⟨EXPR⟩) | a \}$
4. $S = \{EXPR\}$

이 rule을 따르면 $a + a * x$에 대해서 두 가지 경우가 나올 수 있다

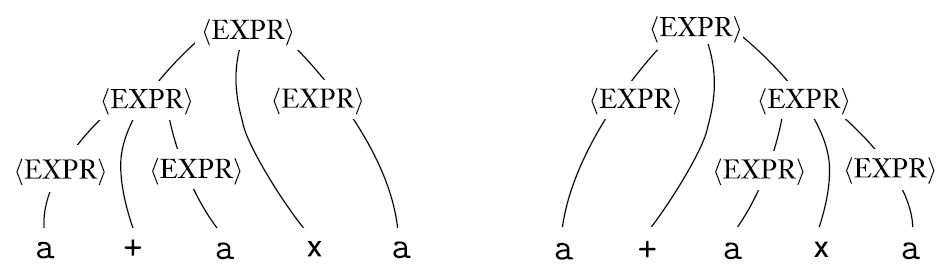
같은 string에 대해서 왼쪽부터 계산한 parse tree가 2개 이상 나오면 ambiguity하다고 한다. 이 왼쪽부터 계산한 것을 leftmost derivation이라고 한다.

String context-free $G$에 대해서 leftmost derivation이 2개 이상 있을 때 ambiguously derive한다. Grammer $G$는 ambigiously한 string이 하나라도 있으면 ambiguous하다.

어떤 context-free language는 ambiguous grammer로 만들어지는 걸 피할 수 없다. 다시 말해 무조건 ambiguous grammer로만 만들어진다. 이를 inherently ambiguous라고 한다.

---

Chomsky Normal Form

Chomsky Normal Form은 다음과 같은 조건을 만족하는 grammer다.

• A → BC
• A → a
• terminal a와 A, B, C은 vcariable이며, B와 C는 start variable이 아니다.
• S → ε, S가 start variable일때만 ε로 바꿀 수 있다.

모든 context-free grammer는 Chomsky Normal Form으로 바꿀 수 있다.